本篇是机器学习小组第四周的学习内容，内容主要摘录自以下学习链接：
模型之母：简单线性回归&最小二乘法
模型之母：多元线性回归
https://mp.weixin.qq.com/s?__biz=MzI4MjkzNTUxMw==&mid=2247483817&idx=1&sn=55812b65b676ec3e1dcc1c2bdf3ccb1b&scene=21#wechat_redirect
还不了解梯度下降法？看完这篇就懂了！
https://mp.weixin.qq.com/s/44p8anqiiQV6XYGqH5u-Ug
我们知道一般的机器学习建模推导思想为：
1.通过分析问题，确定问题的损失函数或者效用函数；
2.然后通过最优化损失函数或者效用函数，获得机器学习的模型。
通过简单和多元线性回归模型推导过程，可以看看是如何验证上述2步的。
简单：是指只有一个样本特征，即只有一个自变量；
线性：是指方程是线性的；
回归：是指用方程来模拟自变量和因变量之间是如何关联的。
简单线性回归，其思想简单，实现容易，并且其结果具有很好的可解释性。在二维平面中，我们需要一条直线最大程度的拟合样本特征和样本数据标记之间的关系。 这条直线的方程就是 y = ax + b。假设我们找到了最佳拟合的直线方程：y = ax + b，则对于每个样本点 ，根据我们的直线方程，预测值为：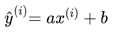
我们希望直线方程能够尽可能地拟合真实情况，也就是说真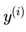值
和预测值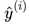
的差距尽量小。只有所有的样本的误差都小，才能证明我们找出的直线方程拟合性好。
通常来说，为了防止正误差值和负误差值相抵的情况，使用绝对值来表示距离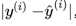
，但是在线性回归中，我们需要找极值，需要函数可导，而
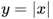不是一个处处可导的函数，因此很自然地想到可以使用：
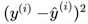。考虑所有样本，我们推导出：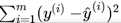
因此我们目标是：已知训练数据样本x、y ，找到a和b的值，使:
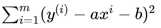
尽可能小，从而得出最佳的拟合方程。到此，我们就实践了步骤1：
通过分析问题，确定问题的损失函数或者效用函数
而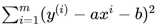
就是简单回归模型的损失函数。这是一个典型的最小二乘法问题（最小化误差的平方）
通过最小二乘法可以求出a、b的表达式：
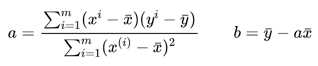
多元线性回归
初学了损失函数和模型评价指标，感觉两者都是用来得到更好的模型。细想了一下，两者的区别是：损失函数描述了单个样本预测值和真实值之间误差的程度。用来度量模型一次预测的好坏。以线性回归为例，损失函数的目的，是为了求得a,b以使模型误差最小。对于回归问题而言，是在求解得到a,b之后，将a，b代入回归模型中求得预测值，通过评价指标MAE，RMSE，MSE计算预测和真实之间的差异，以求得最佳的模型。
原文：https://www.cnblogs.com/favor-dfn/p/11960565.html