每日一题_191207

已知椭圆\(C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) \((a>b>0)\)的左右焦点分别是\(F_1,F_2\),椭圆\(C\)的离心率为\(\dfrac{1}{2}\),且椭圆\(C\)过点\(\left(1,-\dfrac{3}{2}\right)\).
\((1)\) 求椭圆\(C\)的标准方程;
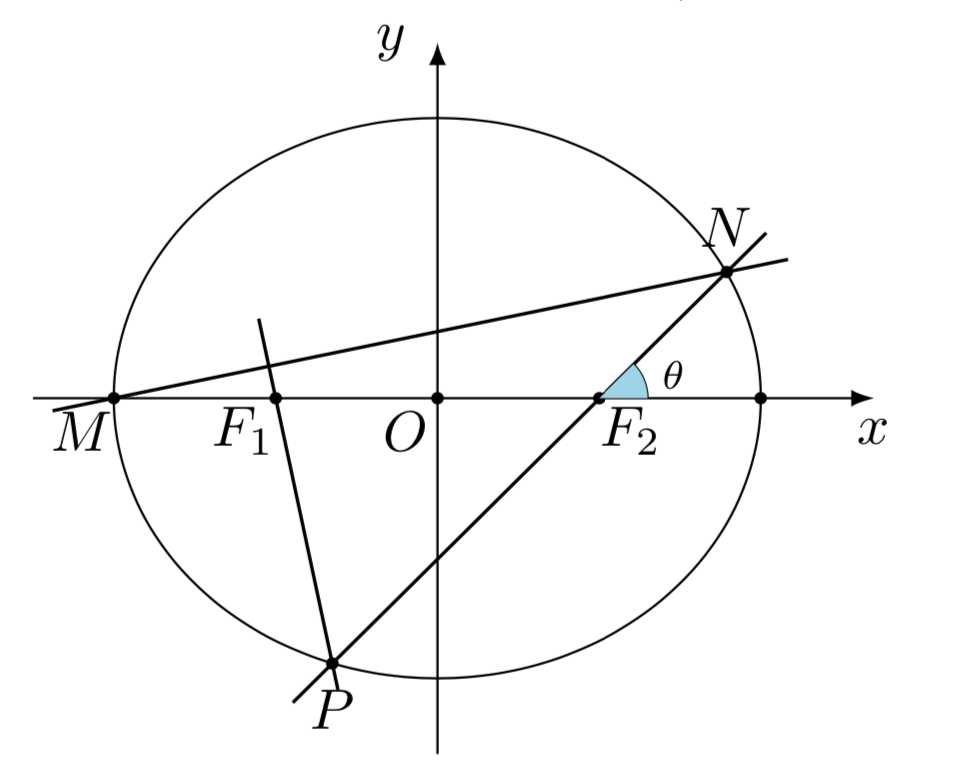
\((2)\) 若直线\(l\)过椭圆\(C\)的左顶点\(M\),且与椭圆\(C\)的另一个交点为\(N\),直线\(NF_2\)与椭圆\(C\)的另一个交点为\(P\),若\(PF_1\perp MN\),求直线\(l\)的方程.
解析:
\((1)\) 由题易得关于\(a,b\)的方程组\[ \dfrac{1}{a^2}+\dfrac{9}{4b^2}=1,\dfrac{b^2}{a^2}=\dfrac{3}{4}. \]
解得\(\left(a,b\right)=\left(2,\sqrt{3}\right)\).从而所求椭圆方程为\(\dfrac{x^2}{4}+\dfrac{y^2}{3}=1\).
\((2)\) 由题,设\(\angle NF_2x=\theta\),则由椭圆的焦半径公式\(\rm{II}\)可得
\(|NF_2|=\dfrac{3}{2+\cos\theta}\),从而

每日一题_191207

原文：https://www.cnblogs.com/Math521/p/11991763.html