介绍下批量梯度下降和随机梯度下降
文中在M个训练样本中,w代表权重,b代表截距,x代表特征,y代表标签,ÿ代表训练值,i代表的第i个样本
使用的是均误方差:
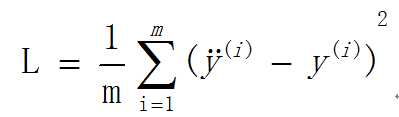
1.批量梯度下降
批量梯度下降法是最原始的形式,它是指在每一次迭代时使用所有样本来进行梯度的更新。从数学上理解如下:
求w关于L的偏导数:
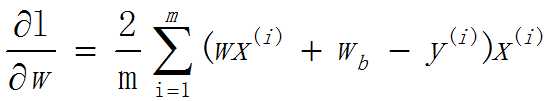
求b关于L的偏导数:
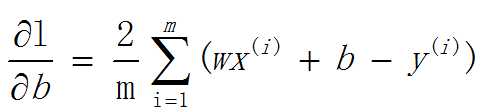
优点:
(1)一次迭代是对所有样本进行计算,此时利用矩阵进行操作,实现了并行。
(2)由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向。当目标函数为凸函数时,BGD一定能够得到全局最优。
缺点:
(1)当样本数目 m 很大时,每迭代一步都需要对所有样本计算,训练过程会很慢。
从迭代的次数上来看,BGD迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下:
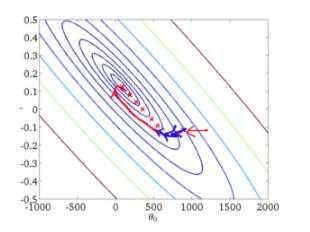
python实现为:
"""批量梯度下降""" #导入数据包 import numpy as np import matplotlib.pyplot as plt #导入数据 datas = np.genfromtxt("csv/data.csv",delimiter=",",skip_header= 1) #导入数据时,需在项目中新建CSV文件,并且去除第一行 x = datas[:,0] y = datas[:,1] plt.scatter(x,y) plt.show()
可以使用matplotlib画图看看结果如下图:
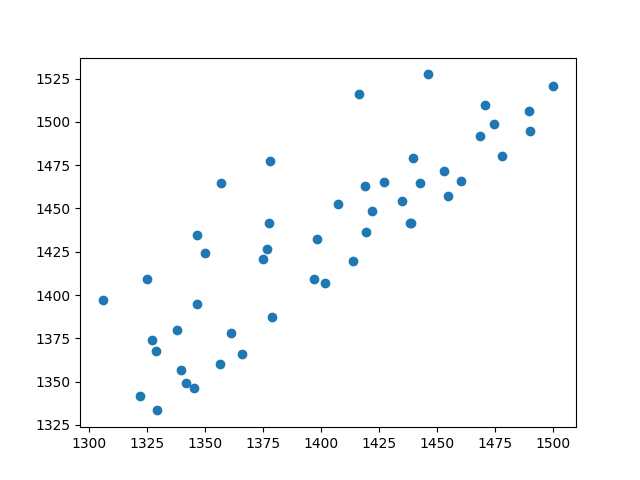
批量梯度下降算法:
#梯度下降 l = len(datas) def param_gra_des(cw,cb,datas,alpha): """ :param cw: 表示每次第i次,w值 :param cb: 表示每次第i次,b值 :param datas: 表示导入的文件 :return:每次更新后的梯度 """ sum_w = 0 #总体的梯度 sum_b = 0 #总体的截距 for i in range(l): x = datas[i,0] y = datas[i,1] sum_w += (cw*x + cb -y)*x #W关于Loss function的导函数总和 sum_b += cw*x + cb -y #关于Loss function的导函数总和 upw = cw - (alpha * sum_w/l)#每一次更新的w值 upb = cb - (alpha *sum_b/l)#每一次更新的w值 return [upw,upb] def step_grd_des(qw,qb,alpha,times,datas): """ :param qw: 表示w的初始值 :param qb: 表示b的初始值 :param alpha: 表示学习率 :param times: 更新的次数 :param data: 表示文件 :return: 最后的权重 """ w = qw b = qb for i in range(times): w = param_gra_des(w,b,datas,alpha)[0] b = param_gra_des(w,b,datas,alpha)[1] return w,b def compute_cost(w,b,datas): total_cost=0 for i in range(l): x=datas[i,0] y=datas[i,1] total_cost += (y-w*x-b)**2 return total_cost/l #一除都是浮点 两个除号是地板除,整型。 如 3 // 4
测试:
#设置起点、学习率 qw = 0 qb = 0 alpha = 0.0000001 times = 5000 #获得训练结果 w,b = step_grd_des(qw,qb,alpha,times,datas) loss_cost = compute_cost(w,b,datas) print("权重为:" + str(w)) print("截距为:" + str(b)) print("平均损失函数:" + str(loss_cost)) plt.scatter(x,y) m_y = w*x + b plt.plot(x,m_y,c = "r") plt.show()
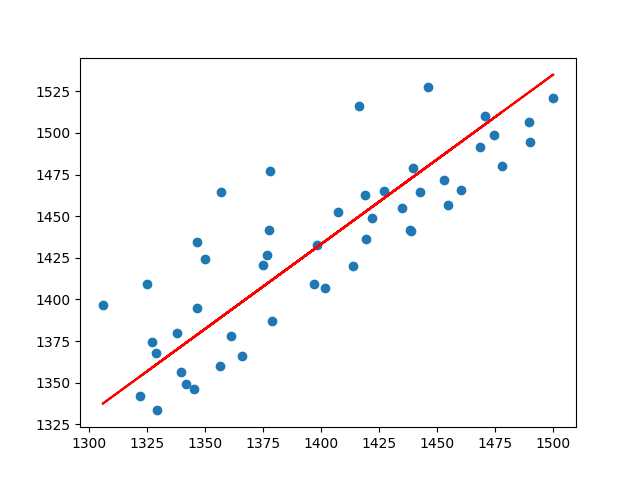
获得结果和图如下:
权重为:1.0180178588402415 截距为:7.997346339384322 平均损失函数:939.0039074472908
2.随机批量下降
随机梯度下降法不同于批量梯度下降,随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。
求w关于L的偏导数:
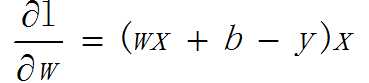
求b关于L的偏导数:
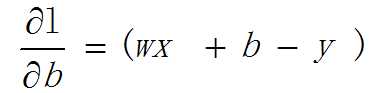
注意:在这里的x和y其实都是m样本中的随机一个样本!!
从迭代的次数上来看,SGD迭代的次数较多,在解空间的搜索过程看起来很盲目。其迭代的收敛曲线示意图可以表示如下:
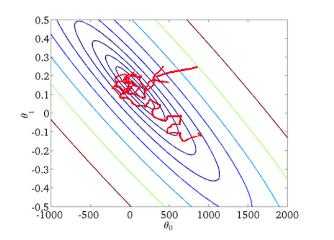
优点:
(1)由于不是在全部训练数据上的损失函数,而是在每轮迭代中,随机优化某一条训练数据上的损失函数,这样每一轮参数的更新速度大大加快。
缺点:
(1)准确度下降。由于即使在目标函数为强凸函数的情况下,SGD仍旧无法做到线性收敛。
(2)可能会收敛到局部最优,由于单个样本并不能代表全体样本的趋势。
(3)不易于并行实现。
python实现为:
#导入数据包 import numpy as np import matplotlib.pyplot as plt import random #导入数据 datas = np.genfromtxt("csv/data.csv",delimiter=",",skip_header= 1) #导入数据时,需在项目中新建CSV文件,并且去除第一行 x = datas[:,0] y = datas[:,1] plt.scatter(x,y)
#plt.show()
#梯度下降 l = len(datas) def param_gra_des(cw,cb,datas,alpha): """ :param cw: 表示第i次,w值 :param cb: 表示第i次,b值 :param datas: 表示导入的文件 :return:每次更新后的梯度 """ i = random.randint(0,l-1)#随机在m样本中产生一个样本 x = datas[i, 0] y = datas[i, 1] upw = cw - (alpha * (cw*x + cb -y)*x)#每一次更新的w值 upb = cb - (alpha *(cw*x + cb -y))#每一次更新的w值 return [upw,upb] def step_grd_des(qw,qb,alpha,times,datas): """ :param qw: 表示w的初始值 :param qb: 表示b的初始值 :param alpha: 表示学习率 :param times: 更新的次数 :param data: 表示文件 :return: 最后的权重 """ w = qw b = qb for i in range(times): w = param_gra_des(w,b,datas,alpha)[0] b = param_gra_des(w,b,datas,alpha)[1] return w,b def compute_cost(w,b,datas): total_cost=0 for i in range(l): x=datas[i,0] y=datas[i,1] total_cost += (y-w*x-b)**2 return total_cost/l #一除都是浮点 两个除号是地板除,整型。 如 3 // 4 #设置位置和学习率以及循环的步数 qw = 0 qb = 0 alpha = 0.00000001 times = 50000 w,b = step_grd_des(qw,qb,alpha,times,datas) loss_cost = compute_cost(w,b,datas) print("权重为:" + str(w)) print("截距为:" + str(b)) print("平均损失函数:" + str(loss_cost)) plt.scatter(x,y) m_y = w*x + b plt.plot(x,m_y,c = "b") plt.show()
结果和截图:
权重为:1.0180178588402415 截距为:7.997346339384322 平均损失函数:939.0039074472908
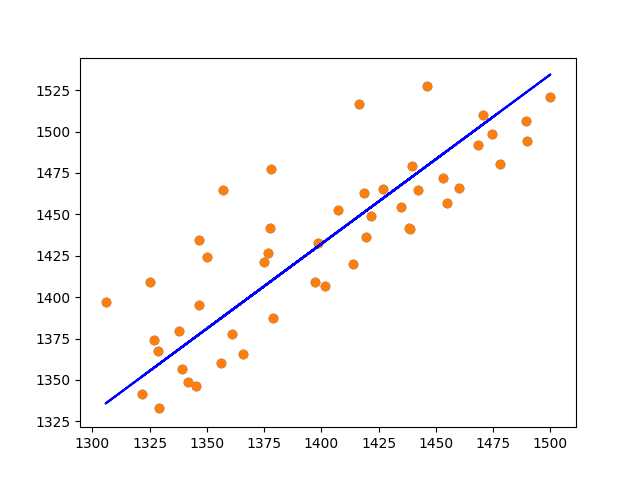
解释一下为什么SGD收敛速度比BGD要快:
答:这里我们假设有30W个样本,对于BGD而言,每次迭代需要计算30W个样本才能对参数进行一次更新,需要求得最小值可能需要多次迭代(假设这里是300);而对于SGD,每次更新参数只需要一个样本,因此若使用这30W个样本进行参数更新,则参数会被更新(迭代)30W次,而这期间,SGD就能保证能够收敛到一个合适的最小值上了。如果都迭代300次的话,那BGD一共运行了300×30W次,而运行了300次。
上面两个代码可以看出:BGD运行了5000次,而SGD使用了50000次获得结果才差不多,如果次数较少的话可能出入较大!
原文:https://www.cnblogs.com/hhxz/p/11992143.html