Appendix 2- Lebesgue integration and Reimann integration

Lebesgue integration and Reimann integration：

Reimann: Split up the axis into equal intervals, then approximate the function within each interval, add up all of those approximate values, and then let the quantization over the time axis become finer.

Lebesgue: Split up the other axis. Start with a zero, quantize into epsilon, 2 epsilon, 3 epsilon and so forth. Making epsilon smaller enough. Lower bound.

Rules:

• l  Whenever the Riemann integral exists, the Lebesgue integral also exists and has the same value.
• l  The familiar rules for calculating Riemann integrals also apply for Lebesgue integrals.
• l  For some very weird functions, the Lebesgue integral exists, but the Riemann integral does not. (i.e., Dirichlet function)
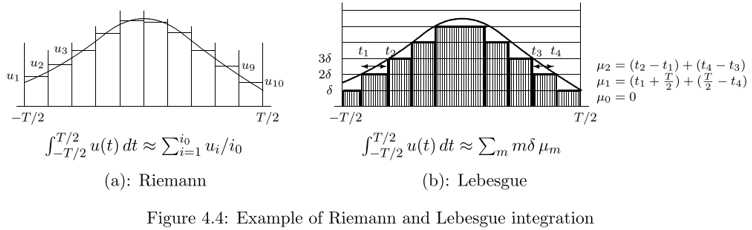
• l  There are also exceptionally weird functions for which not even the Lebesgue integral exists.

Appendix 2- Lebesgue integration and Reimann integration

原文：https://www.cnblogs.com/yangyang827847/p/11994525.html