课程:《程序设计与数据结构》
班级: 1823
姓名: 赵沛凝
学号:20182301
实验教师:王志强
实验日期:2019年12月2日
必修/选修: 必修
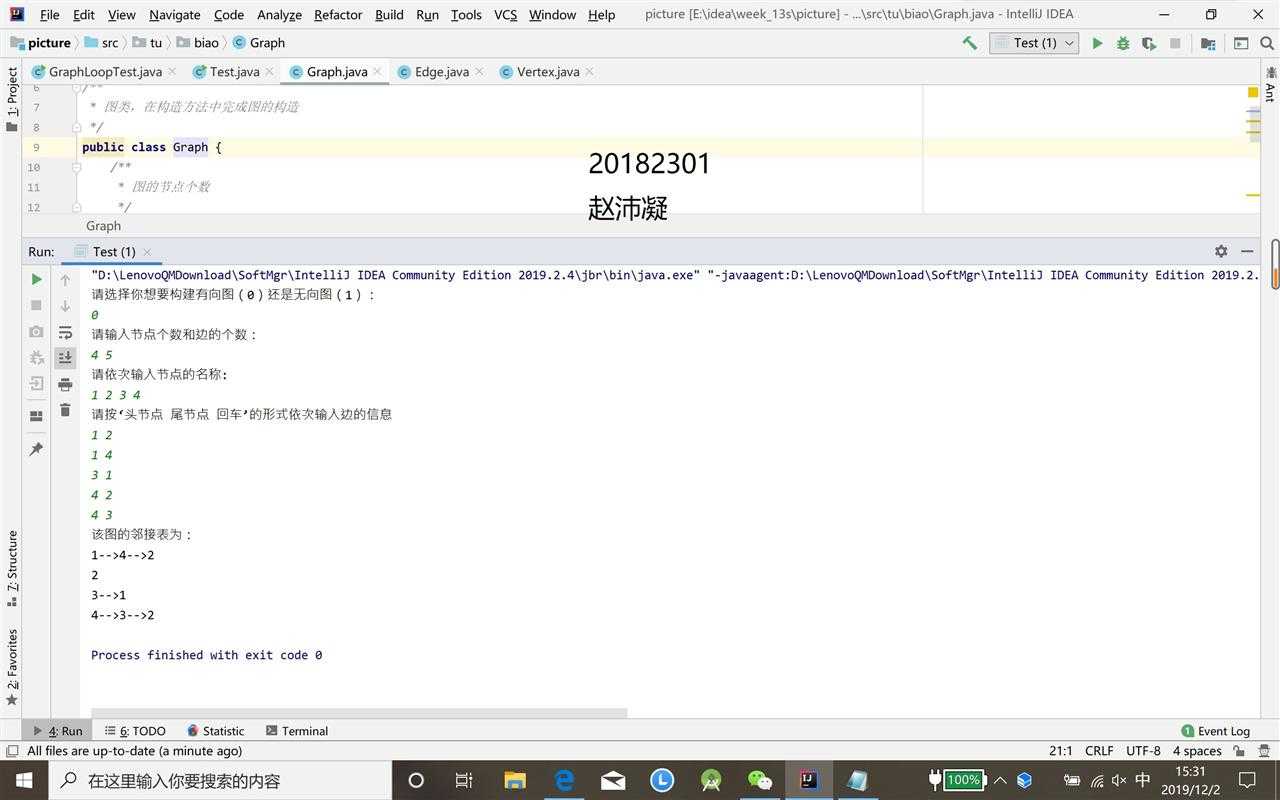
System.out.println("请按‘头节点 尾节点 回车’的形式依次输入边的信息");
for (int i=0;i<edgeNum;i++){
String preName = scan.next();
String folName = scan.next();
Vertex preV = getVertex(preName);
Vertex folV = getVertex(folName);
if (preV == null || folV == null){ System.out.println("输入错误,输入了不存在的顶点!请重新输入");
i--;
continue;
}
Edge edge = new Edge();
edge.tailName = folName;
//将边加入到节点的链表中去
edge.broEdge = preV.edgeLink;//循环
preV.edgeLink = edge;//放在出始地的后面
Edge edgeelse = new Edge();
edgeelse.tailName = preName;
edgeelse.broEdge = folV.edgeLink;
folV.edgeLink = edgeelse;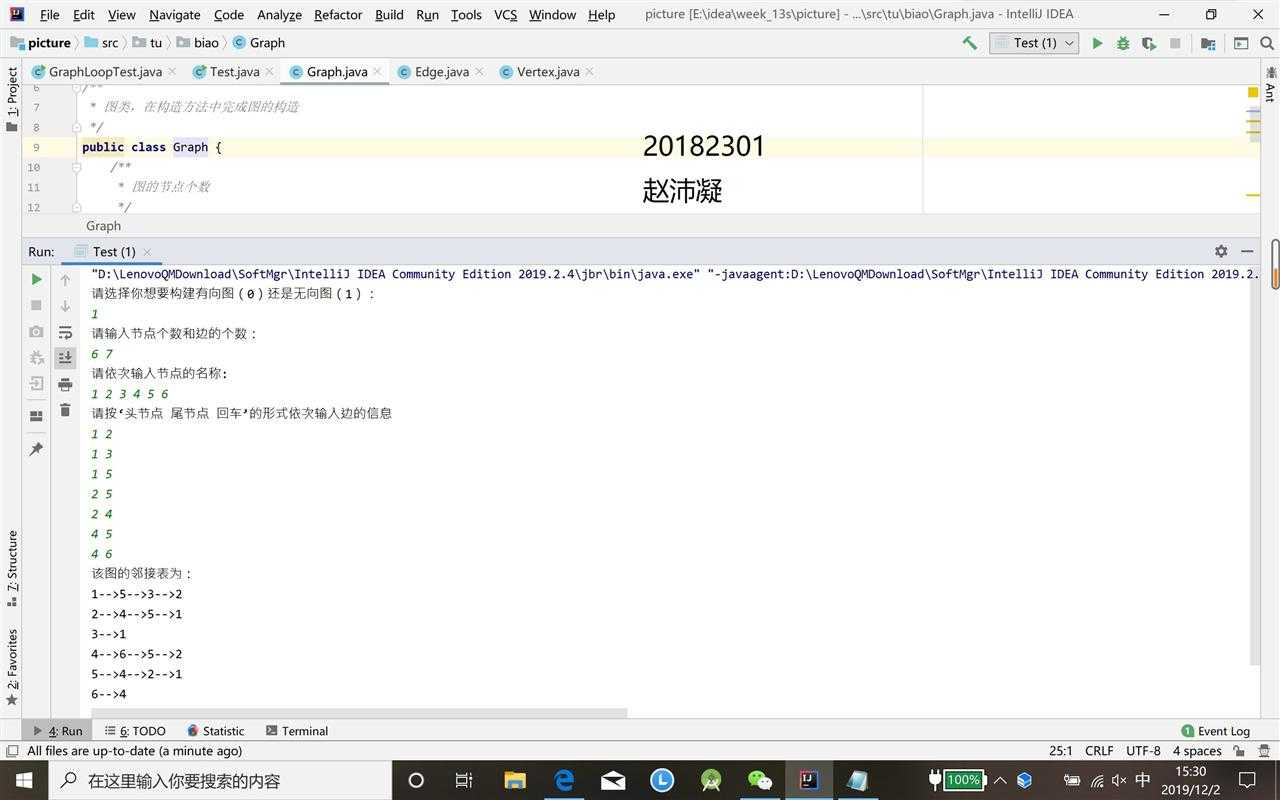
private Queue<String> queue = new LinkedList<String>();
private Map<String, Boolean> status = new HashMap<String, Boolean>();
public void BFSSearch(String startPoint) {
//1.把起始点放入queue;
queue.add(startPoint);
status.put(startPoint, false);
bfsLoop();
}
private void bfsLoop() {
// 1) 从queue中取出队列头的点;更新状态为已经遍历。
String currentQueueHeader = queue.poll(); //出队
status.put(currentQueueHeader, true);
System.out.println(currentQueueHeader);
// 2) 找出与此点邻接的且尚未遍历的点,进行标记,然后全部放入queue中。
List<String> neighborPoints = graph.get(currentQueueHeader);
for (String poinit : neighborPoints) {
if (!status.getOrDefault(poinit, false)) { //未被遍历
if (queue.contains(poinit)) continue;
queue.add(poinit);
status.put(poinit, false);
}
}
if (!queue.isEmpty()) { //如果队列不为空继续遍历
bfsLoop();
}
} private Stack<String> stack = new Stack<String>();
public void DFSSearch(String startPoint) {
stack.push(startPoint);
status.put(startPoint, true);
dfsLoop();
}
private void dfsLoop() {
if(stack.empty()){
return;
}
//查看栈顶元素,但并不出栈
String stackTopPoint = stack.peek();
// 2) 找出与此点邻接的且尚未遍历的点,进行标记,然后全部放入queue中。
List<String> neighborPoints = graph.get(stackTopPoint);
for (String point : neighborPoints) {
if (!status.getOrDefault(point, false)) { //未被遍历
stack.push(point);
status.put(point, true);
dfsLoop();
}
}
String popPoint = stack.pop();
System.out.println(popPoint);
}
startNode = directedGraph.get(startNodeLabel);
if (startNode == null) {
startNode = new Vertex(startNodeLabel);
directedGraph.put(startNodeLabel, startNode);
}
endNode = directedGraph.get(endNodeLabel);
if (endNode == null) {
endNode = new Vertex(endNodeLabel);
directedGraph.put(endNodeLabel, endNode);
}
e = new Edge(endNode);//每读入一行代表一条边
startNode.adjEdges.add(e);//每读入一行数据,起始顶点添加一条边
endNode.inDegree++;//每读入一行数据,终止顶点入度加1 Queue<Vertex> queue = new LinkedList<>();// 拓扑排序中用到的栈,也可用队列.
//扫描所有的顶点,将入度为0的顶点入队列
Collection<Vertex> vertexs = directedGraph.values();
for (Vertex vertex : vertexs)
if(vertex.inDegree == 0)
queue.offer(vertex);
while(!queue.isEmpty()){
Vertex v = queue.poll();
System.out.print(v.vertexLabel + " ");
count++;
for (Edge e : v.adjEdges)
if(--e.endVertex.inDegree == 0)
queue.offer(e.endVertex);
}
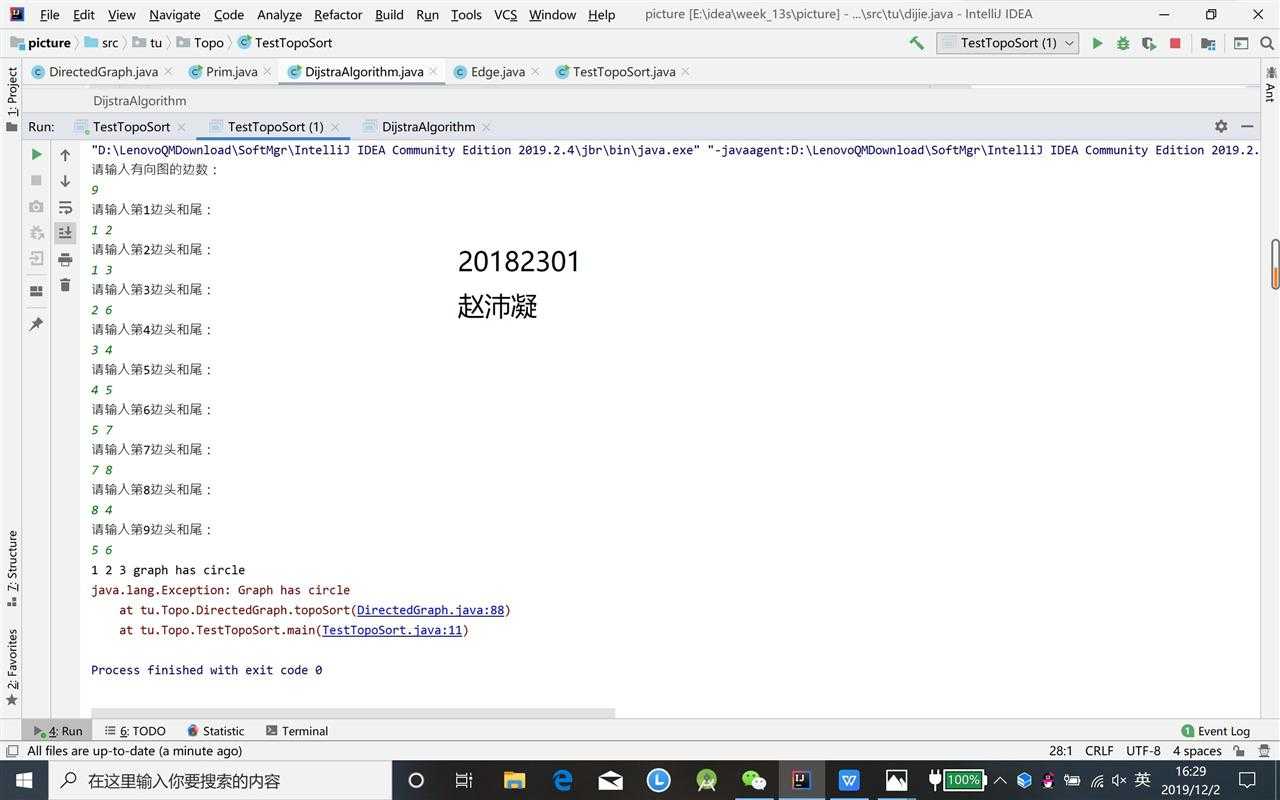
if(count != directedGraph.size()){
throw new Exception("Graph has circle");
}

public Edge(int i,int j,int w){
this.i=i;
this.j=j;
this.w=w;
}
@Override
public int compareTo(Object o) {
Edge to=(Edge)o;
if(this.w>to.w) return 1;
else if(this.w==to.w) return 0;
else return -1;
}
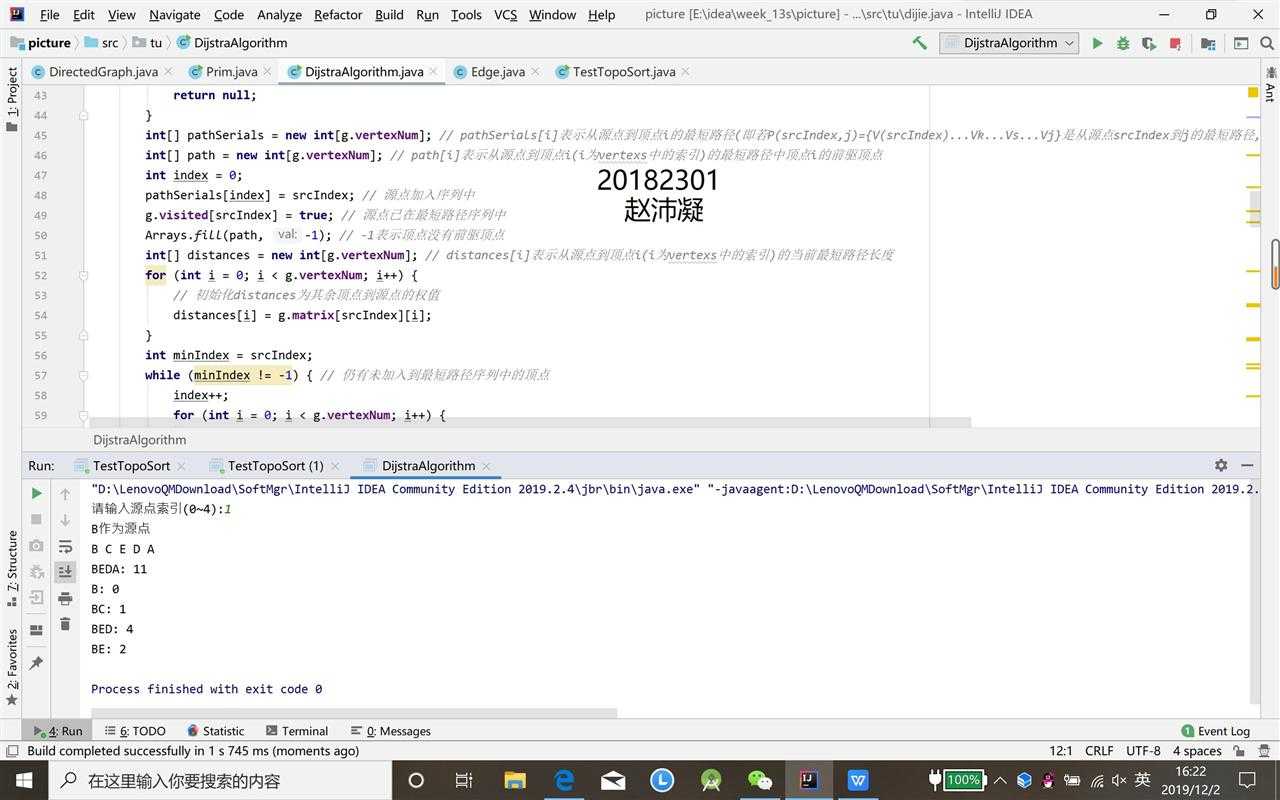
public static Info dijkstra(Graph g, int srcIndex) {
if(srcIndex < 0 || srcIndex >= g.vertexNum){
return null;
}
int[] pathSerials = new int[g.vertexNum]; // pathSerials[i]表示从源点到顶点i的最短路径(即若P(srcIndex,j)={V(srcIndex)...Vk...Vs...Vj}是从源点srcIndex到j的最短路径,则有P(srcIndex,j)=P(srcIndex,k)+P(k,s)+P(s,j))
int[] path = new int[g.vertexNum]; // path[i]表示从源点到顶点i(i为vertexs中的索引)的最短路径中顶点i的前驱顶点
int index = 0;
pathSerials[index] = srcIndex; // 源点加入序列中
g.visited[srcIndex] = true; // 源点已在最短路径序列中
Arrays.fill(path, -1); // -1表示顶点没有前驱顶点
int[] distances = new int[g.vertexNum]; // distances[i]表示从源点到顶点i(i为vertexs中的索引)的当前最短路径长度
for (int i = 0; i < g.vertexNum; i++) {
// 初始化distances为其余顶点到源点的权值
distances[i] = g.matrix[srcIndex][i];
}
int minIndex = srcIndex;
while (minIndex != -1) { // 仍有未加入到最短路径序列中的顶点
index++;
for (int i = 0; i < g.vertexNum; i++) {
if (!g.visited[i]) { // 更新仍未加入到最短路径序列中的顶点的从源点到它的值
// 这些仍未加入到最短路径序列中的顶点的distances[i]值为(刚加入的顶点minIndex的distances[minIndex]与minIndex到顶点i之和)与(顶点minIndex刚加入之前源点到i的距离值distances[i])两者之间的较小者
distances[i] = Math.min(distances[i], distances[minIndex] + g.matrix[minIndex][i]);
// 如果当前顶点i的distances[i]值为新加入的顶点minIndex,则顶点i的前驱为minIndex,否则不变
if(distances[i] == distances[minIndex] + g.matrix[minIndex][i] && distances[i] != Integer.MAX_VALUE / 2){ // distances[i] != Integer.MAX_VALUE / 2表示仍不可达,就没有前驱
path[i] = minIndex;
}
}
}
minIndex = indexOf(g, distances); // 选出的最小顶点
if(minIndex == -1){
break;
}
pathSerials[index] = minIndex; // 刚选出的最小顶点加入到最短路径序列中
g.visited[minIndex] = true;
}
return new Info(distances, pathSerials, getPathOfAll(path, pathSerials));
}public static int indexOf(Graph g, int[] distances) {
int min = Integer.MAX_VALUE / 3;
int minIndex = -1; // 当前数组distances剩余元素最小值(-1表示无剩余元素)--剩余元素就是仍未加入到最短路径序列中的顶点
for(int i = 0; i < g.vertexNum; i++){
if(!g.visited[i]){ // 如果i顶点仍未加入到最短路径序列中
if(distances[i] < min){
min = distances[i];
minIndex = i;
}
}
}
return minIndex;
}public static int[] getPath(int[] path, int i){
Stack<Integer> s = new Stack<Integer>();
s.push(i);
int pre = path[i];
while(pre != -1){
s.push(pre);
pre = path[pre];
}
int size = s.size();
int[] pathOfVertex = new int[size];
while(!s.isEmpty()){
pathOfVertex[size - s.size()] = s.pop();
}
return pathOfVertex;
}public static class Info{
private int[] distances; // 源点到各个顶点的最短距离
private int[] pathSerials; // 整个最短路径序列
private ArrayList<int[]> paths; // 源点到各个顶点的确切最短路径序列
public Info(int[] distances, int[] pathSerials, ArrayList<int[]> paths) {
this.distances = distances;
this.pathSerials = pathSerials;
this.paths = paths;
}
}
问题1:在第一题中,无向图的邻接链表总是出错,为什么?
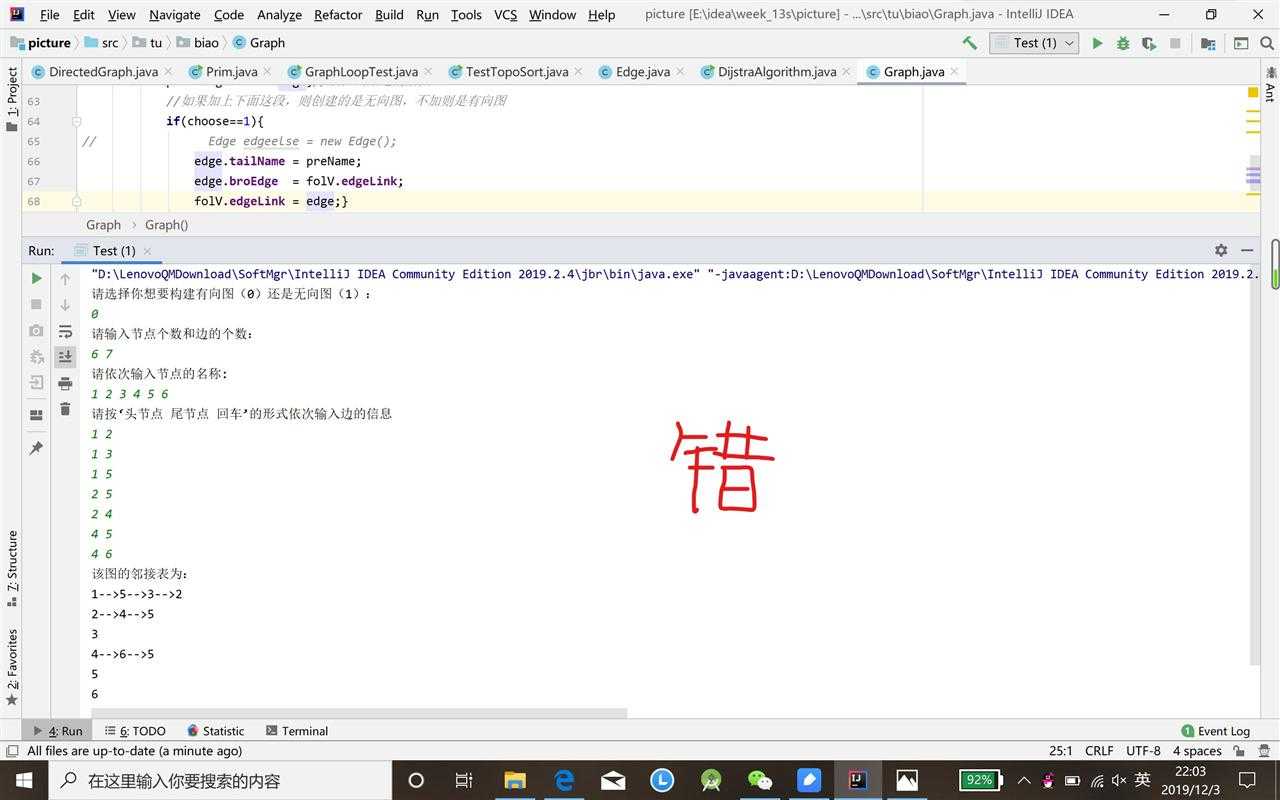
edge.tailName = preName;
edge.broEdge = folV.edgeLink;
folV.edgeLink = edge;Edge edgeelse = new Edge();
edgeelse.tailName = preName;
edgeelse.broEdge = folV.edgeLink;
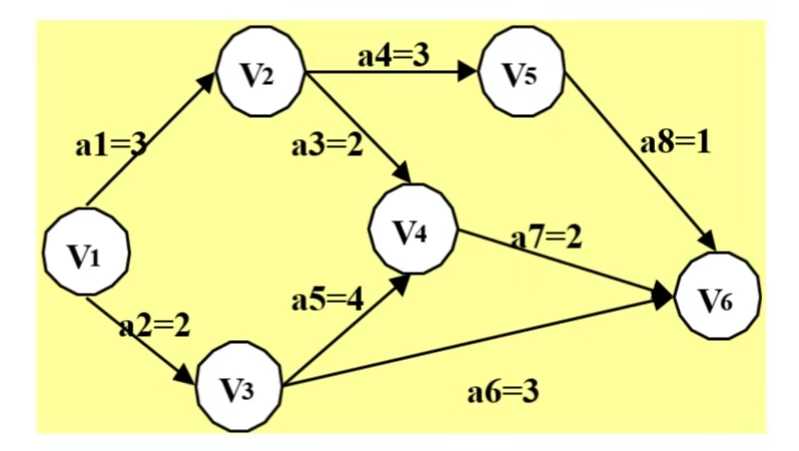
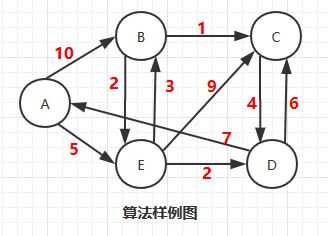
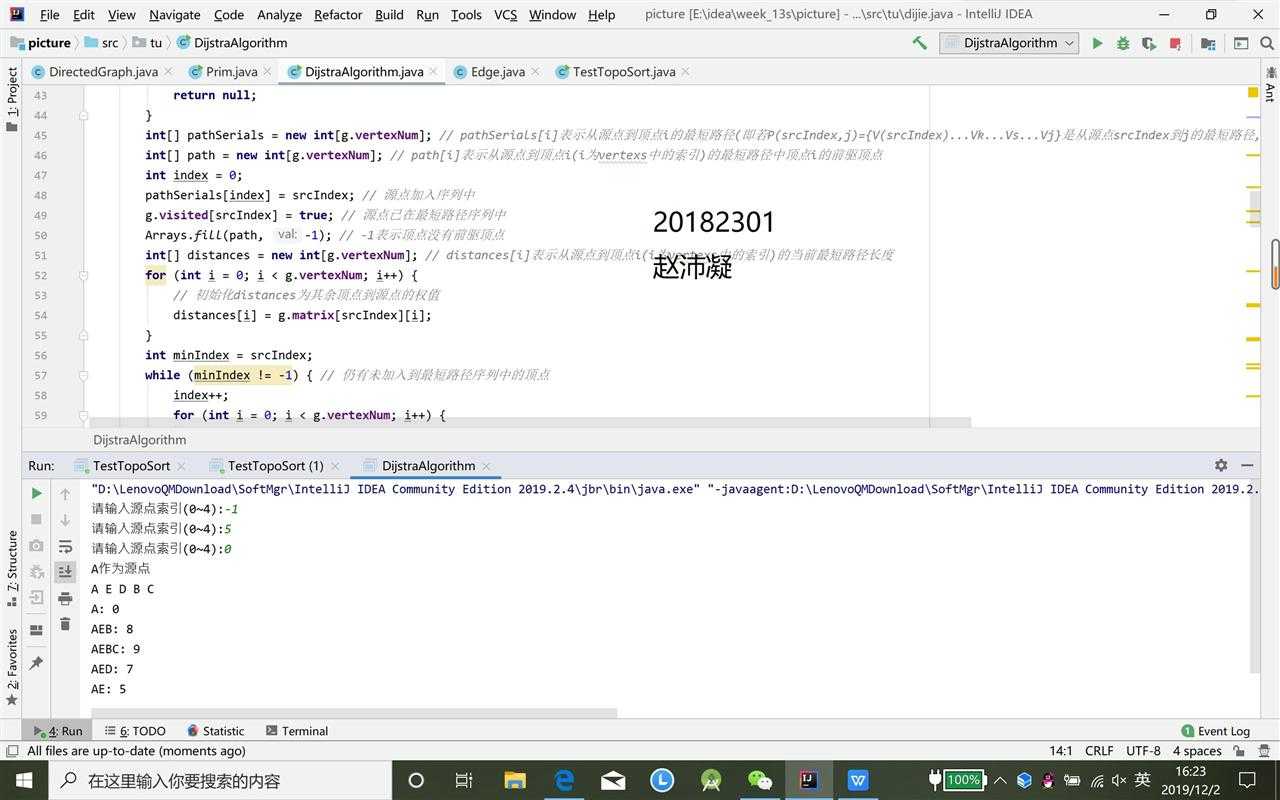
folV.edgeLink = edgeelse;将源节点(即节点0)加入S中,对shortest和visited数组进行更新。
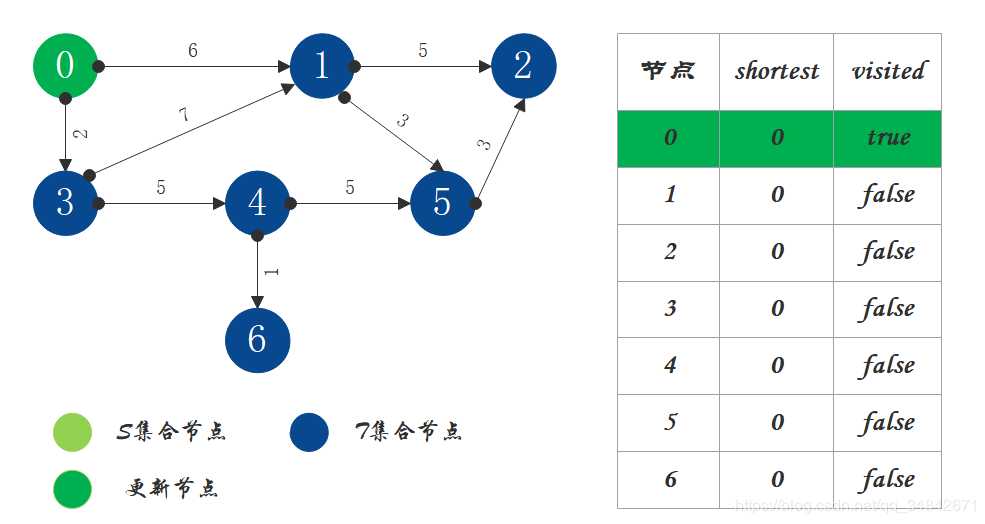
S中现有节点0,源节点可达T中的节点1和节点3,节点0->节点1距离为6,节点0->节点3距离为2,按距离从小到大排序,因此选择将节点3加入S中。更新源点将节点3作为中间节点到达其它节点的距离。
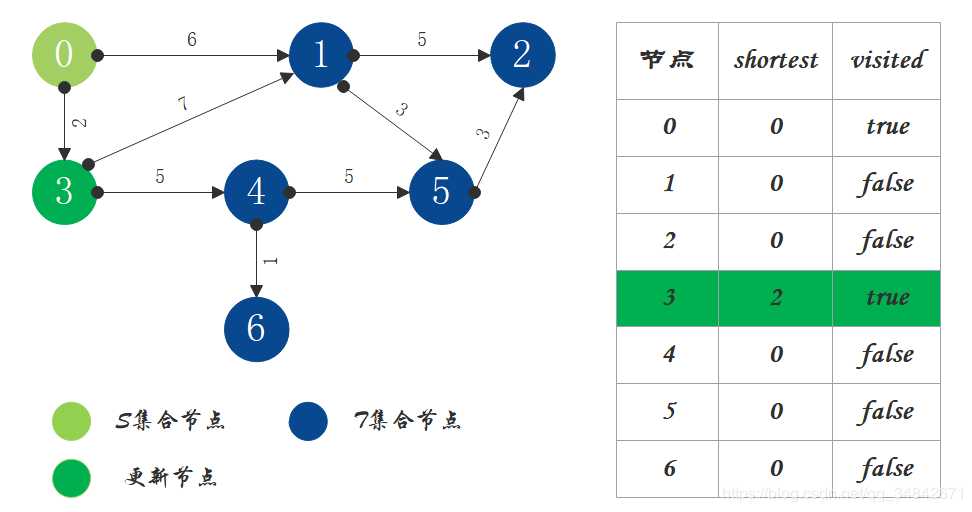
S中现有节点0和节点3,源节点可达T中的节点1和4,节点0->节点1距离为6,节点0->节点4距离为7,按距离从小到大排序,因此选择将节点1加入S中。更新源点将节点1作为中间节点到达其它节点的距离。
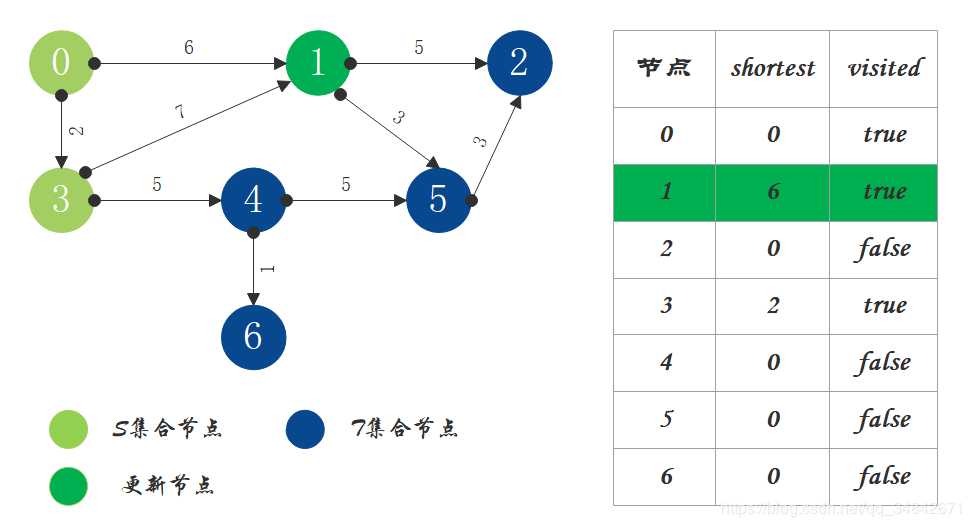
S中现有节点0、1、3,源节点可达T中的节点2、4、5,0->2距离为11,0->4距离为7,0->5距离为9,按距离从小到大排序,因此选择将节点4加入S中。更新源点将节点4作为中间节点到达其它节点的距离。
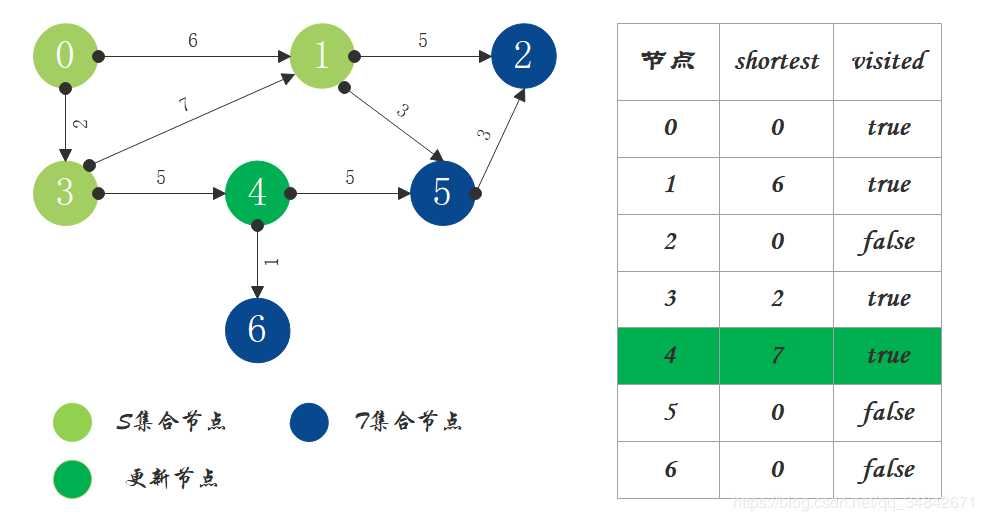
S中现有节点0、1、3、4,源节点可达T中的节点2、5、6,0->2距离为11,0->5距离为9,0->6距离为8,按距离从小到大排序,因此选择将节点6加入S中。更新源点将节点6作为中间节点到达其它节点的距离。
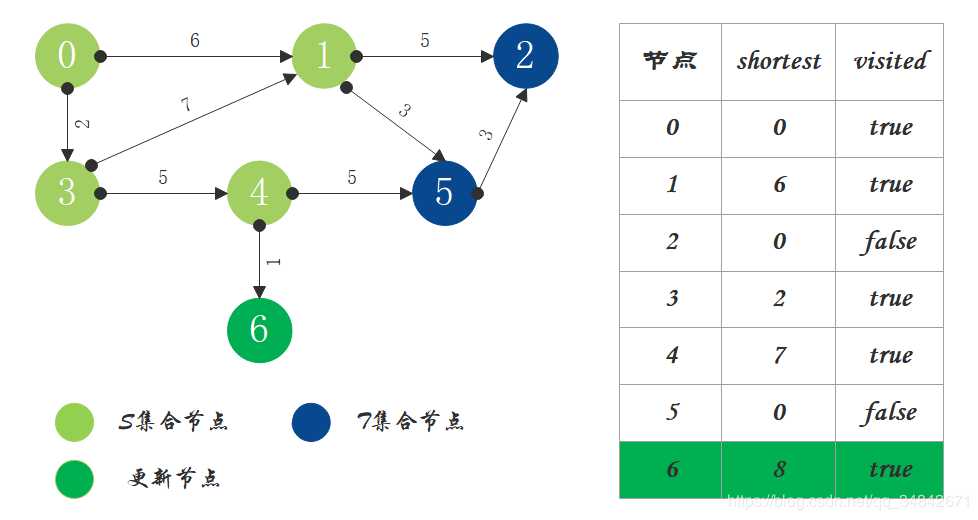
S中现有节点0、1、3、4、6,源节点可达T中的节点2、5,0->2距离为11,0->5距离为9,按距离从小到大排序,因此选择将节点5加入S中。更新源点将节点5作为中间节点到达其它节点的距离。
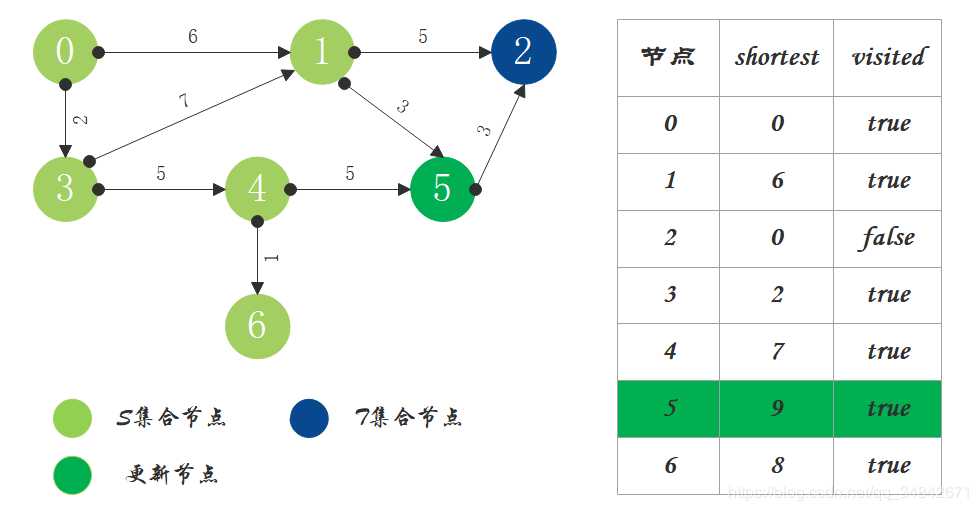
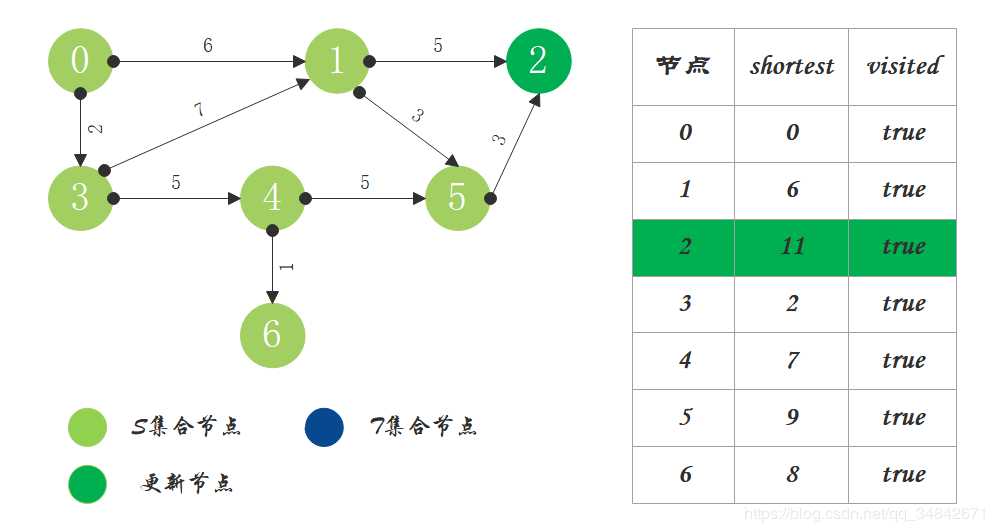
T中只剩下节点2,0->2距离为11,将节点2加入S中。
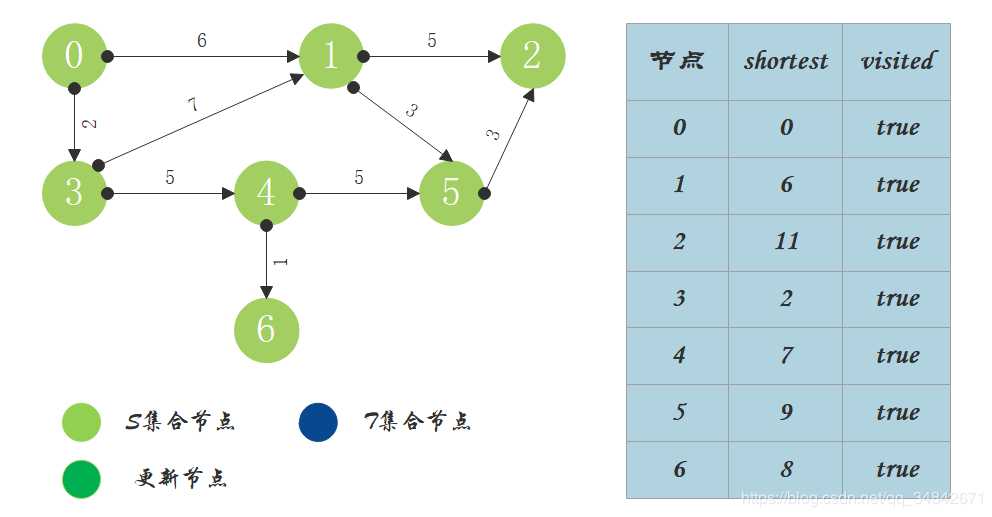
如果每次都把老师讲的进行实践,那么实验也不会很费力。以后在学习过程中,也要循序渐进。
20182301 2019-2020-1 《数据结构与面向对象程序设计》实验9报告
原文:https://www.cnblogs.com/zhaopeining/p/11980007.html