学号20182304 2019-2020-1 《数据结构与面向对象程序设计》实验九报告

课程：《程序设计与数据结构》
班级： 1823
姓名： 张子正
学号：20182304
实验教师：王志强
实验日期：2019年12月7日
必修/选修： 必修

1.实验内容

• 初始化：根据屏幕提示（例如：输入1为无向图，输入2为有向图）初始化无向图和有向图（可用邻接矩阵，也可用邻接表），图需要自己定义（顶点个数、边个数，建议先在草稿纸上画出图，然后再输入顶点和边数）
• 图的遍历：完成有向图和无向图的遍历（深度和广度优先遍历）
• 完成有向图的拓扑排序，并输出拓扑排序序列或者输出该图存在环
• 完成无向图的最小生成树（Prim算法或Kruscal算法均可），并输出
• 完成有向图的单源最短路径求解（迪杰斯特拉算法）

2. 实验过程及结果

• 初始化相对容易，需要注意邻接矩阵与邻接数组的定义。有向图与无向图的差距主要在邻接矩阵上
  
  
  
• 图的遍历：完成有向图和无向图的遍历（深度和广度优先遍历）
• 只要建立邻接矩阵和对应的标志数组，就可以相对容易的实现。DFS利用递归来实现比较易懂，DFS非递归就是将需要的递归的元素利用一个栈Stack来实现，以达到递归时候的顺序。
  BFS遍历相对复杂一些

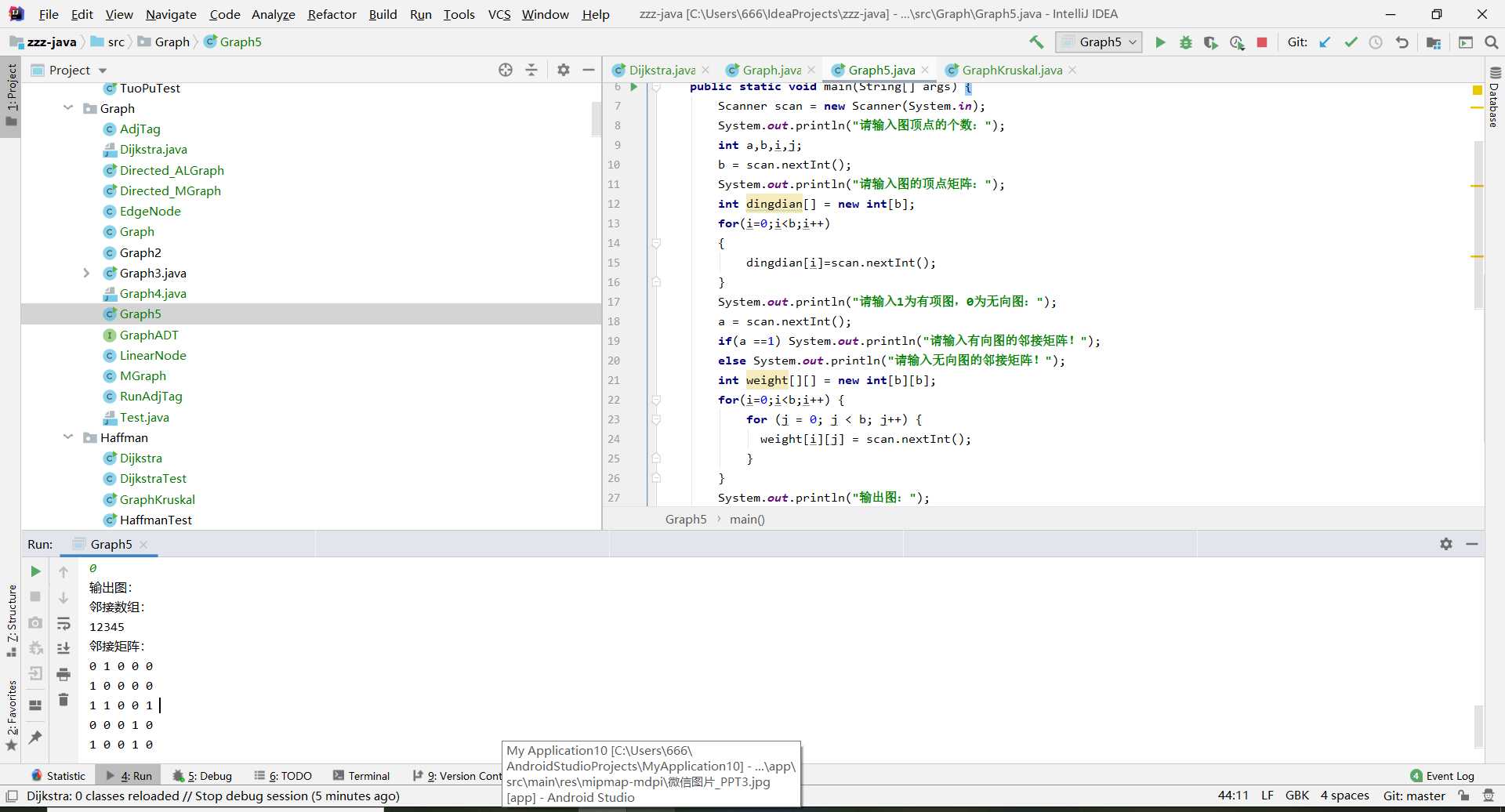
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;


public class Graph {
//节点个数
    private static int number = 8;
//创立访问标志数组的布尔型数组
    private boolean[] flag;

//创立要遍历节点的数组
    private int[] num= {1,2,3,4,5,6,7,8};
//创立这几个数字的邻接矩阵
    private int[][] edges = {
            /*{0, 1, 1, 0, 0, 0, 0, 0},
            {1, 0, 0, 1, 1, 0, 0, 0},
            {1, 0, 0, 0, 0, 1, 1, 0},
            {0, 1, 0, 0, 0, 0, 0, 1},
            {0, 1, 0, 0, 0, 0, 0, 1},
            {0, 0, 1, 0, 0, 0, 1, 0},
            {0, 0, 1, 0, 0, 1, 0, 0},
            {0, 0, 0, 1, 1, 0, 0, 0},*/
        {0, 1, 1, 0, 0, 0, 0, 0},
        {0, 0, 0, 1, 1, 0, 0, 0},
        {0, 0, 0, 0, 0, 1, 1, 0},
        {0, 0, 0, 0, 0, 0, 0, 1},
        {0, 0, 0, 0, 0, 0, 0, 0},
        {0, 0, 0, 0, 0, 0, 1, 0},
        {0, 0, 0, 0, 0, 0, 0, 0},
        {0, 0, 0, 0, 1, 0, 0, 0},

    };

    void DFSTraverse() {
        //设置一个和数字个数同等大小的布尔数组
        flag = new boolean[number] ;
        //从顶点开始，实现深度遍历
        for (int i = 0; i < number; i++) {
            if (flag[i] == false) {
                // 如果当前顶点没有被访问，进入DFS
                DFS(i);
            }
        }
    }
//完成一次遍历，直到后面无连接节点
    void DFS(int i) {
        // 标记第num[i]个节点被访问
        flag[i] = true;
        //将该节点打印
        System.out.print(num[i] + " ");
        //寻找与num[i]节点相连的下一个访问节点
        for (int j = 0; j < number; j++) {
            //从标志数组第0位开始顺序查找，如果这一点未被访问，且与第num[i]个节点相连
            if (flag[j] == false && edges[i][j] == 1) {
                //递归
                DFS(j);
            }
        }
    }

    void DFS_Map(){
        flag = new boolean[number];
        Stack<Integer> stack =new Stack<Integer>();
        for(int i=0;i<number;i++){
            if(flag[i]==false){
                flag[i]=true;
                System.out.print(num[i]+" ");
                stack.push(i);
            }
            while(!stack.isEmpty()){
                int k = stack.pop();
                for(int j=0;j<number;j++){
                    if(edges[k][j]==1&&flag[j]==false){
                        flag[j]=true;
                        System.out.print(num[j]+" ");
                        stack.push(j);
                        break;
                    }
                }

            }
        }
    }

    void BFS_Map(){
        flag = new boolean[number];
        Queue<Integer> queue = new LinkedList<Integer>();
        for(int i=0;i<number;i++){
            if(flag[i]==false){
                flag[i]=true;
                System.out.print(num[i]+" ");
                queue.add(i);
                while(!queue.isEmpty()){
                    int k=queue.poll();
                    for(int j=0;j<number;j++){
                        if(edges[k][j]==1&&flag[j]==false){
                            flag[j] = true;
                            System.out.print(num[j]+" ");
                            queue.add(j);
                        }
                    }
                }
            }
        }
    }


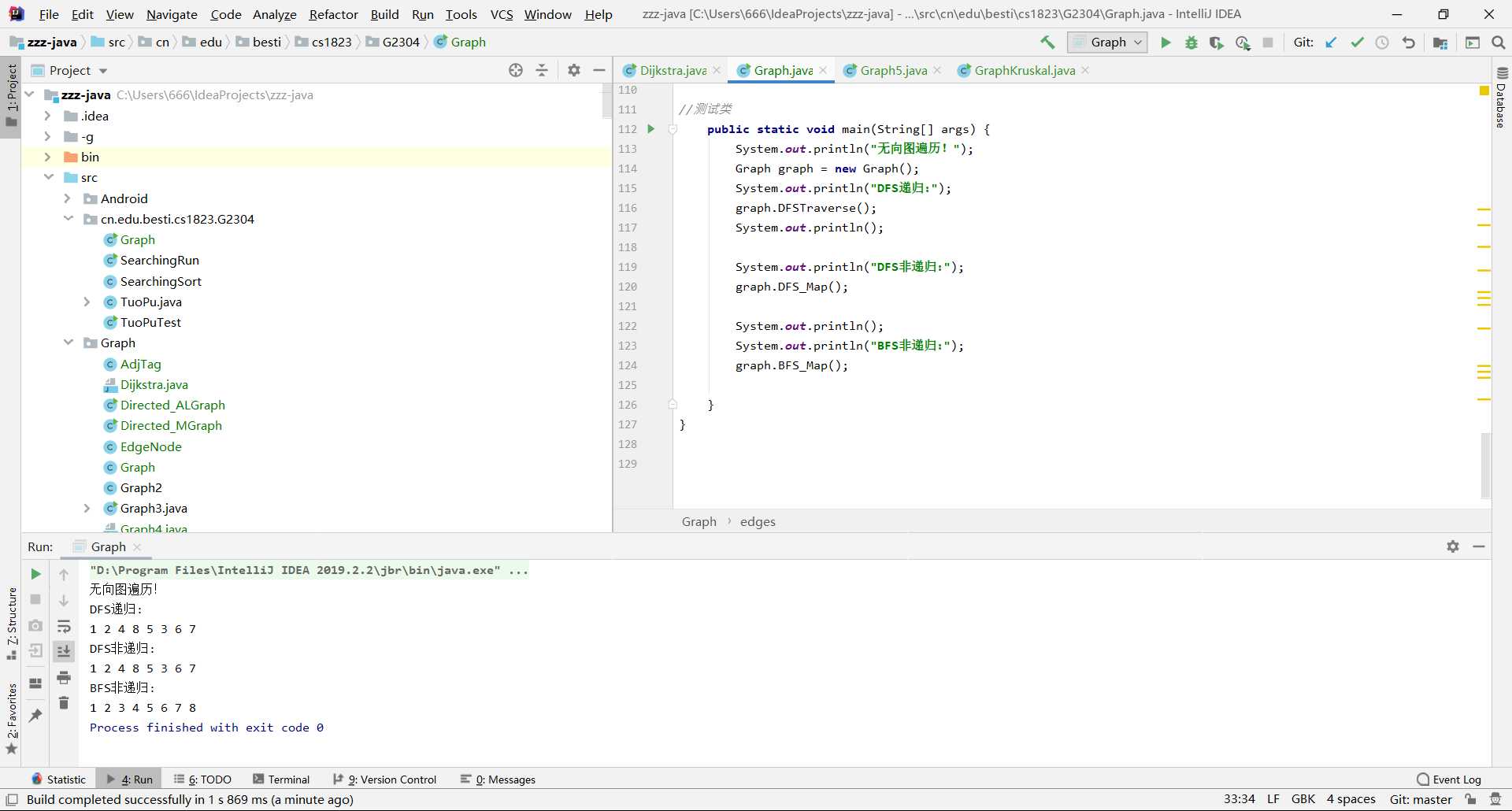
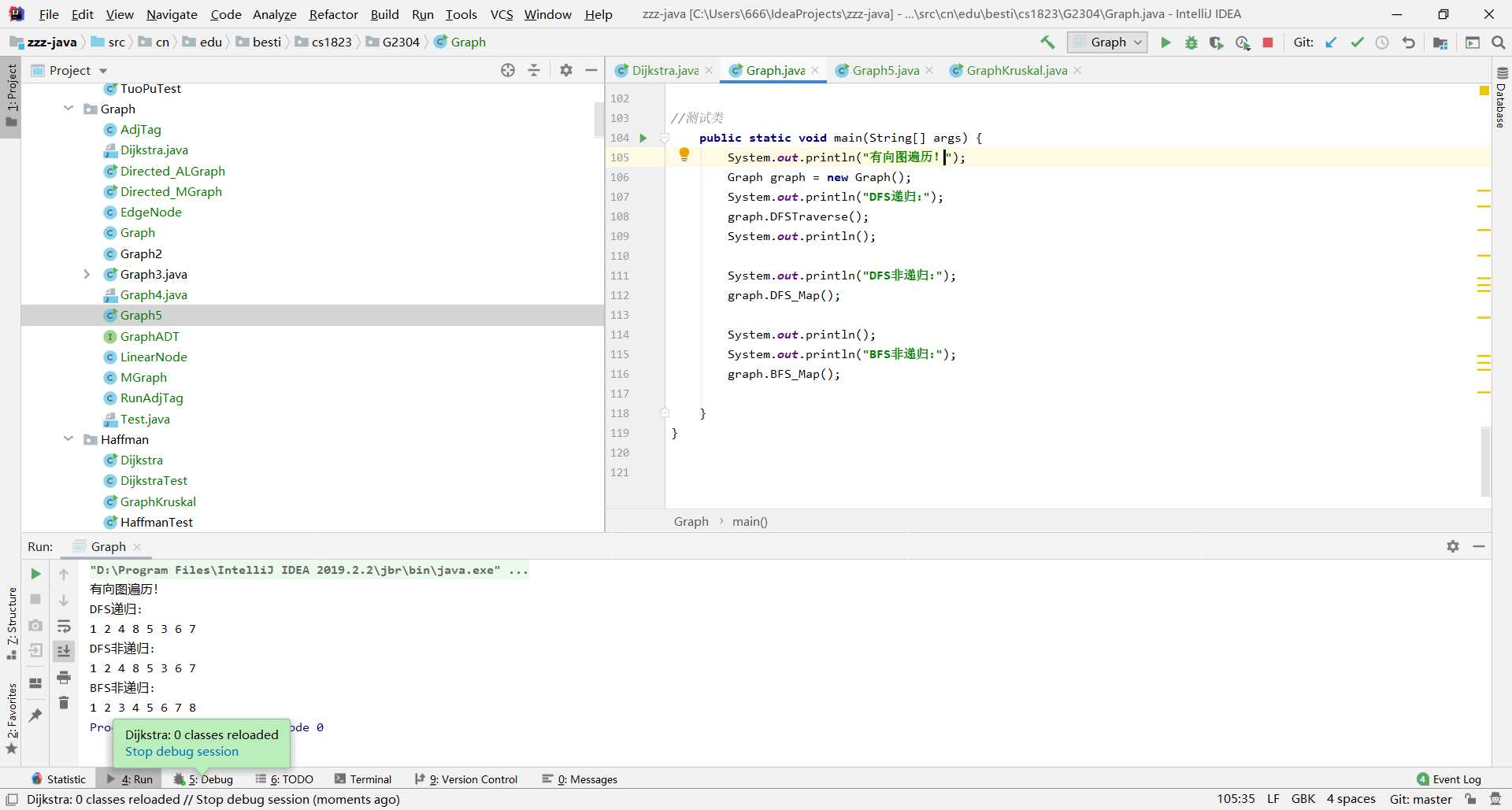
//测试类
    public static void main(String[] args) {
        System.out.println("有向图遍历！");
        Graph graph = new Graph();
        System.out.println("DFS递归:");
        graph.DFSTraverse();
        System.out.println();

        System.out.println("DFS非递归:");
        graph.DFS_Map();

        System.out.println();
        System.out.println("BFS非递归:");
        graph.BFS_Map();

    }
} 

• 完成有向图的拓扑排序，并输出拓扑排序序列或者输出该图存在环(这个实践作业中已经完成了)

• 完成无向图的最小生成树（Prim算法或Kruscal算法均可），并输出
  • 我使用的是Kruscal算法
    
    
• 完成有向图的单源最短路径求解（迪杰斯特拉算法）
  
  
  

3. 实验过程中遇到的问题和解决过程

• 问题1：kruskal(克鲁斯卡尔)算法的实现思路是什么，应该如何具体实现
• 问题1解决方案：
  • 现将所有边进行权值的从小到大排序
  • 定义一个一维数组代表连接过的边，数组的下标为边的起点，值为边的终点
  • 按照排好序的集合用边对顶点进行依次连接，连接的边则存放到一维数组中
  • 用一维数组判断是否对已经连接的边能构成回路，有回路则无效，没回路则是一条有效边
  • 重复3，4直至遍历完所有的边为止，即找到最小生成树
• 问题2：Dijkstra的作用是什么，如何具体实现Dijkstra算法
• 问题2解决方案：迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。
  • 具体实现思路详见代码

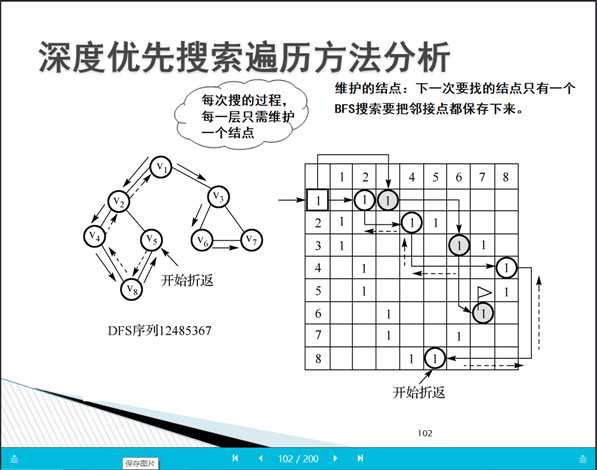
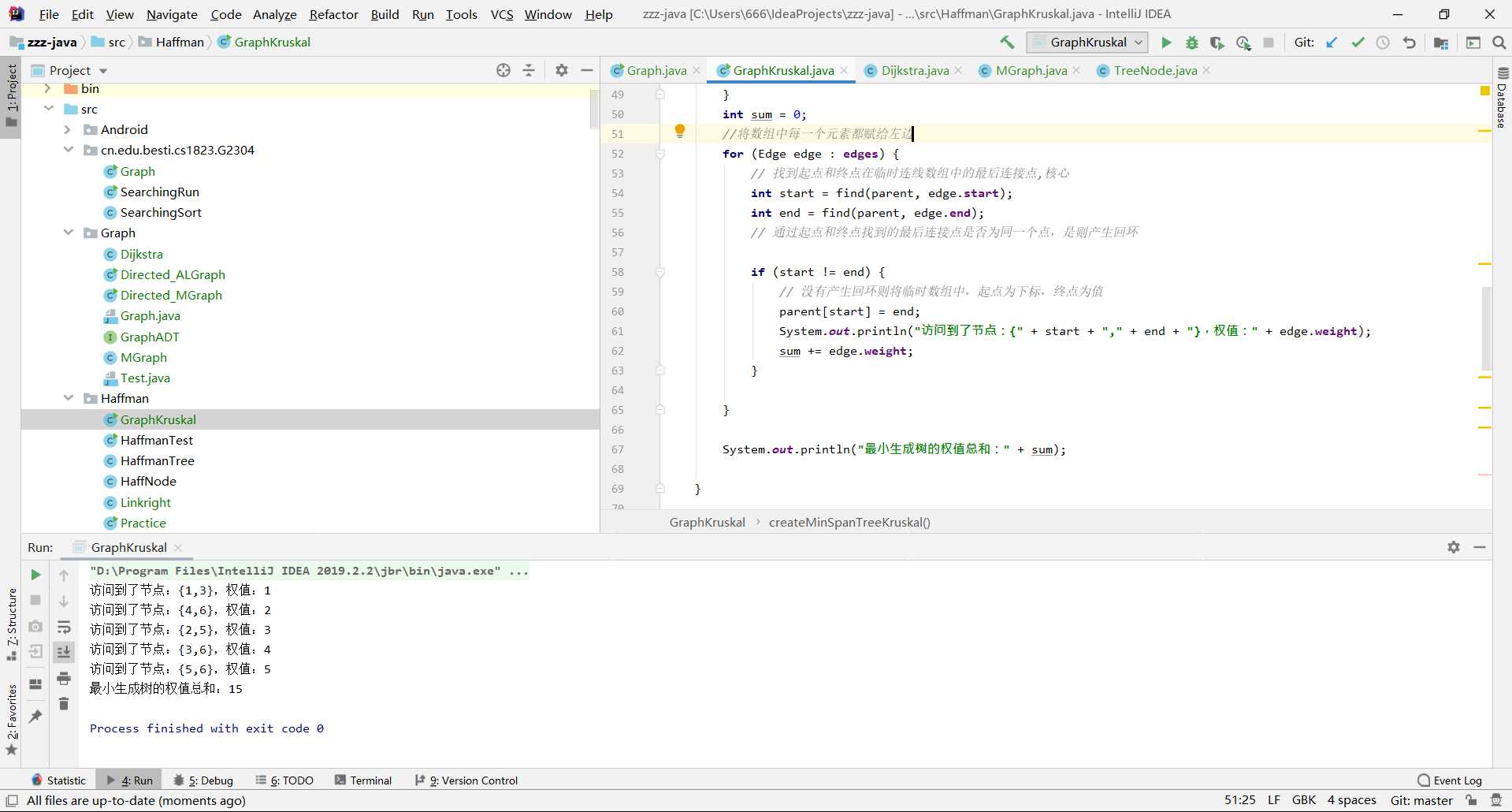
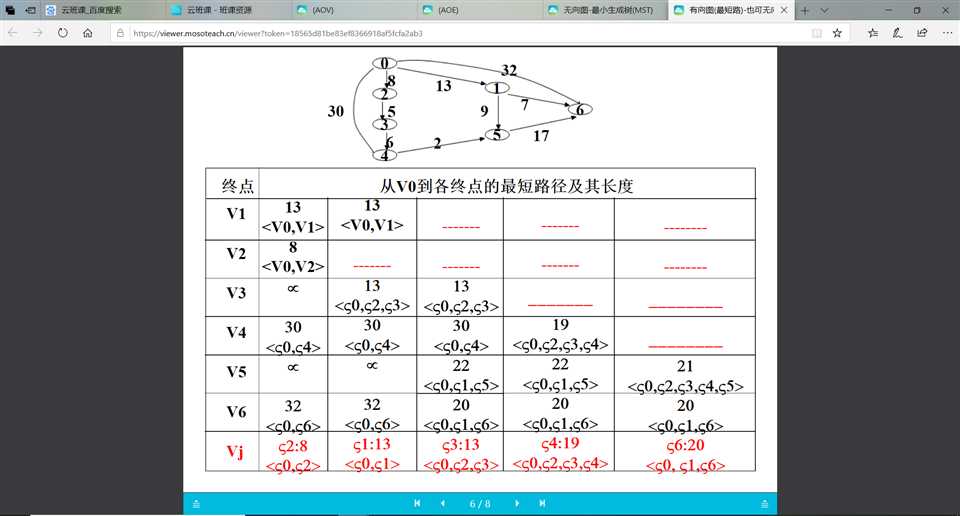
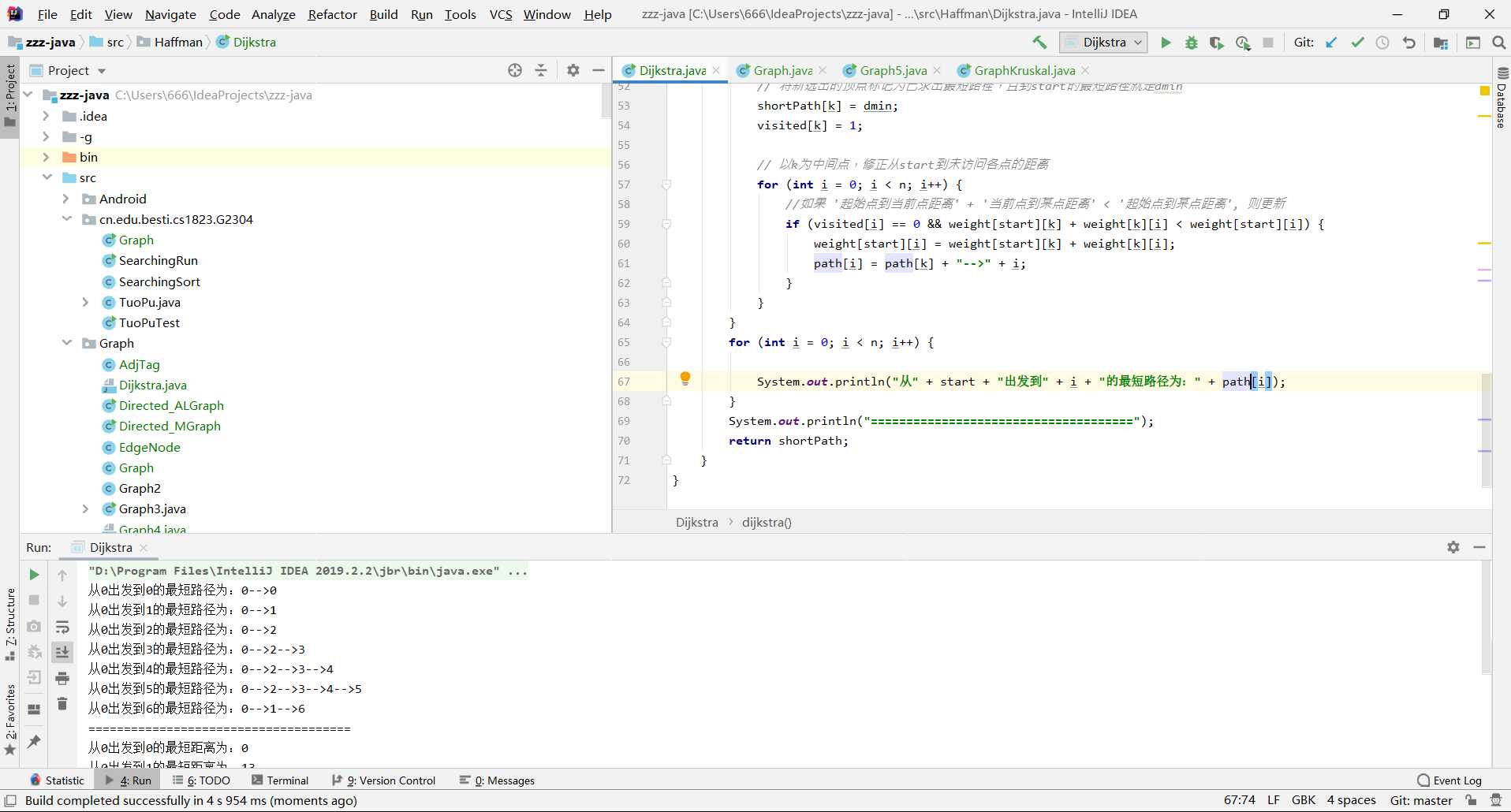
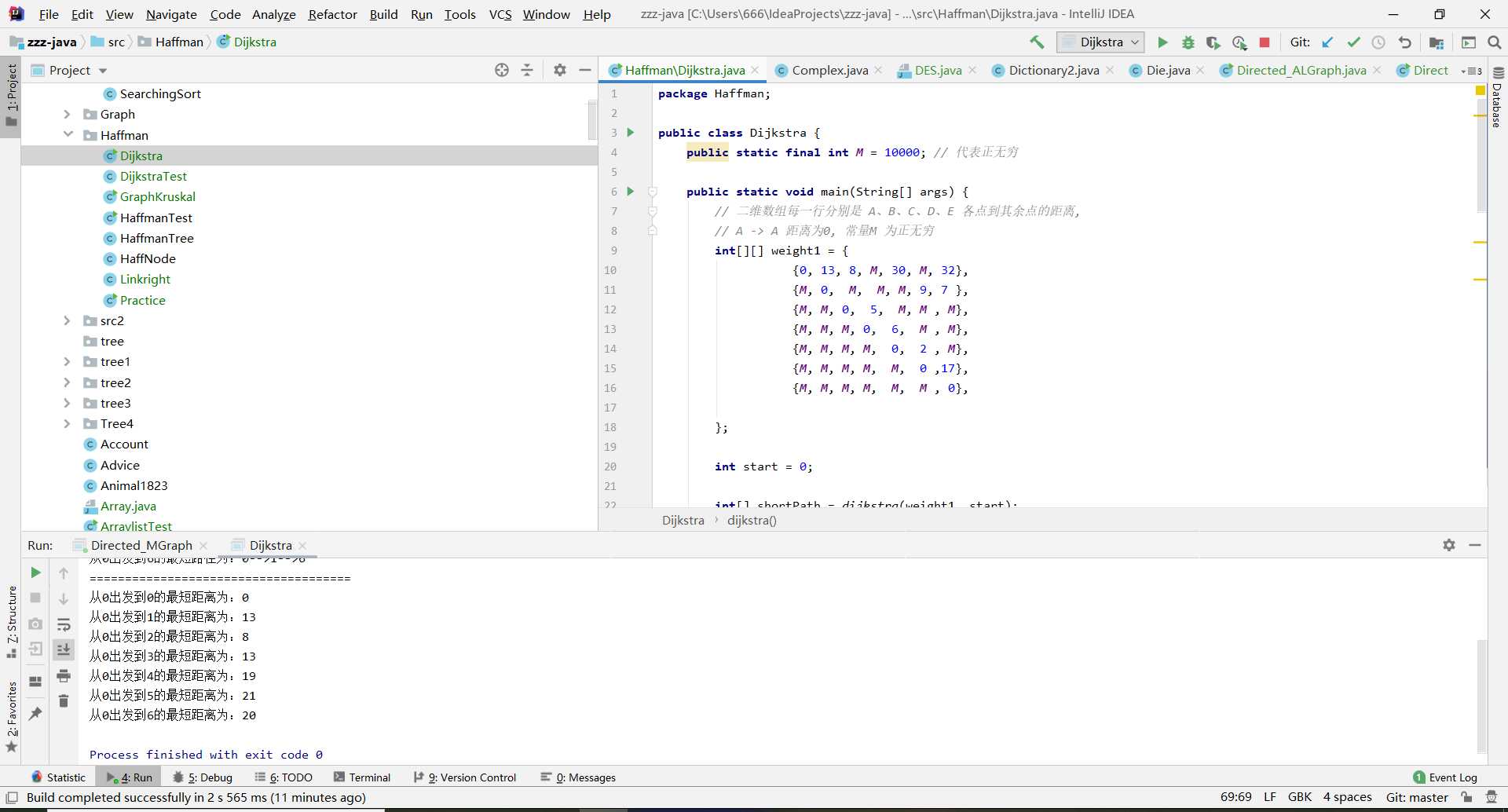
  public class Dijkstra {
  public static final int M = 10000; // 代表正无穷
  
  public static void main(String[] args) {
      // 二维数组每一行分别是 A、B、C、D、E 各点到其余点的距离,
      // A -> A 距离为0, 常量M 为正无穷
      int[][] weight1 = {
                 {0, 13, 8, M, 30, M, 32},
                 {M, 0,  M,  M, M, 9, 7 },
                 {M, M, 0,  5,  M, M , M},
                 {M, M, M, 0,  6,  M , M},
                 {M, M, M, M,  0,  2 , M},
                 {M, M, M, M,  M,  0 ,17},
                 {M, M, M, M,  M,  M , 0},
  
      };
  
      int start = 0;
  
      int[] shortPath = dijkstra(weight1, start);
  
      for (int i = 0; i < shortPath.length; i++)
          System.out.println("从" + start + "出发到" + i + "的最短距离为：" + shortPath[i]);
  }
  
  public static int[] dijkstra(int[][] weight, int start) {
      // 接受一个有向图的权重矩阵，和一个起点编号start（从0编号，顶点存在数组中）
      // 返回一个int[] 数组，表示从start到它的最短路径长度
      int n = weight.length; // 顶点个数
      int[] shortPath = new int[n]; // 保存start到其他各点的最短路径
      String[] path = new String[n]; // 保存start到其他各点最短路径的字符串表示
      for (int i = 0; i < n; i++)
          path[i] = new String(start + "-->" + i);
      int[] visited = new int[n]; // 标记当前该顶点的最短路径是否已经求出,1表示已求出
  
      // 初始化，第一个顶点已经求出
      shortPath[start] = 0;
      visited[start] = 1;
  
      for (int count = 1; count < n; count++) { // 要加入n-1个顶点
          int k = -1; // 选出一个距离初始顶点start最近的未标记顶点
          int dmin = Integer.MAX_VALUE;
          for (int i = 0; i < n; i++) {
              if (visited[i] == 0 && weight[start][i] < dmin) {
                  dmin = weight[start][i];
                  k = i;
              }
          }
  
          // 将新选出的顶点标记为已求出最短路径，且到start的最短路径就是dmin
          shortPath[k] = dmin;
          visited[k] = 1;
  
          // 以k为中间点，修正从start到未访问各点的距离
          for (int i = 0; i < n; i++) {
              //如果 '起始点到当前点距离' + '当前点到某点距离' < '起始点到某点距离', 则更新
              if (visited[i] == 0 && weight[start][k] + weight[k][i] < weight[start][i]) {
                  weight[start][i] = weight[start][k] + weight[k][i];
                  path[i] = path[k] + "-->" + i;
              }
          }
      }
      for (int i = 0; i < n; i++) {
  
          System.out.println("从" + start + "出发到" + i + "的最短路径为：" + path[i]);
      }
      System.out.println("=====================================");
      return shortPath;
  }
  }

其他（感悟、思考等）

• 因为我负责录制了讲解其中几个算法的视频，所以对这次的实验内容相对熟悉，完成起来也较为轻松。重点在于掌握算法的思路，再进一步编程实现

参考资料

• 《Java程序设计与数据结构教程（第二版）》

• 《Java程序设计与数据结构教程（第二版）》学习指导

• ...

实验九

原文：https://www.cnblogs.com/acgacg/p/12007950.html