leetcode回溯算法--基础难度

都是直接dfs，算是巩固一下

电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

思路

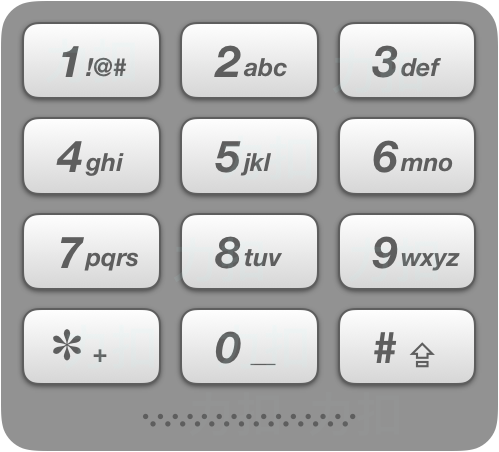
一直搜索，到终点判断是否已经出现，未出现则加入集合

代码

class Solution {
    set<string>s;
    map<char,string>m;
public:
    
    void dfs(string d, string cur, int step){
        if(step>d.size()){
            return;
        }
        if(step==d.size()){
            if(s.count(cur)>0){
                return;
            }else{
                s.insert(cur);
            }
        }
        string tmp=m[d[step]];
        for(int i=0;i<tmp.size();++i){
            dfs(d,cur+tmp[i],step+1);
        }
    }
    
    vector<string> letterCombinations(string digits) {
        m.insert(make_pair('2',"abc"));
        m.insert(make_pair('3',"def"));
        m.insert(make_pair('4',"ghi"));
        m.insert(make_pair('5',"jkl"));
        m.insert(make_pair('6',"mno"));
        m.insert(make_pair('7',"pqrs"));
        m.insert(make_pair('8',"tuv"));
        m.insert(make_pair('9',"wxyz"));
        string s1;
        vector<string>ans;
        if(digits.size()==0){
            return ans;
        }
        dfs(digits,s1,0);
        for(auto i = s.begin(); i!=s.end();++i){
            ans.push_back(*i);
        }
        return ans;
    }
};

生成括号

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

思路

第一个肯定是左括号，接着搜索，每个位置可能是"("或者")"，搜索时注意左右括号的数量关系

代码

class Solution {
    vector<string>ans;
    bool ok(const string&s){
        stack<char>st;
        for(int i=0;i<s.size();++i){
            if(s[i]=='('){
                st.push(s[i]);
            }else{
                if(st.empty()){
                    return false;
                }else{
                    char c=st.top();
                    if(c!='(')return false;
                    else st.pop();
                }
            }
        }
        return st.empty();
    }
public:
    void dfs(string cur,int L,int R,int total){
        if(L+R>total)return;
        if(abs(L-R)>total-L-R)return;
        if(L+R==total){
            if(L!=R){
                return;
            }else{
                if(ok(cur)){
                    ans.push_back(cur);   
                }
                return;
            }
        }
        dfs(cur+'(',L+1,R,total);
        dfs(cur+')',L,R+1,total);
    }
    vector<string> generateParenthesis(int n) {
        if(n==0)return ans;
        dfs("(",1,0,2*n);
        return ans;
    }
};

全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:

[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

思路

dfs，用一个数组记录下已经访问过的元素即可
该方法对于有重复元素也有效

代码

class Solution {
public:
    void dfs(int step,vector<int>cur,vector<int>&nums,int*vis,vector<vector<int>>&ans){
        if(step>nums.size())return;
        if(step==nums.size()){
            ans.push_back(cur);
            return;
        }
        for(int i=0;i<nums.size();++i){
            if(!vis[i]){
                vis[i]=1;
                cur.push_back(nums[i]);
                dfs(step+1,cur,nums,vis,ans);
                vis[i]=0;
                cur.pop_back();
            }
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> ans;
        if(nums.size()==0)return ans;
        int vis[nums.size()];
        memset(vis,0,sizeof(vis));
        vector<int>tmp;
        dfs(0,tmp,nums,vis,ans);
        return ans;
    }
};

子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:

[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

思路

跟全排列很相似，但是不能重复（[1，2]和[2,1]是相同的子集)
所以搜索的范围限制在left之后，即只会从大往小([1,2],[1,3],[2,3])
这样就不会重复了

代码

class Solution {
public:
    void dfs(int step, vector<int> cur,int left,int*vis, int limit,const vector<int>&nums, vector<vector<int>>&ans){
        if(step>limit)return;
        if(step==limit){
            ans.push_back(cur);
            return;
        }
        for(int i=left;i<nums.size();++i){
            if(!vis[i]){
                vis[i]=1;
                cur.push_back(nums[i]);
                dfs(step+1,cur,i+1,vis,limit,nums,ans);
                cur.pop_back();
                vis[i]=0;
            }
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> ans;
        vector<int>emp;
        ans.push_back(emp);
        int vis[nums.size()];
        if(nums.size()==0)return ans;
        for(int i=1;i<=nums.size();++i){
            memset(vis,0,sizeof(vis));
            dfs(0,emp,0,vis,i,nums,ans);
        }
        return ans;
    }
};

单词搜索

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例:

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

给定 word = "ABCCED", 返回 true.
给定 word = "SEE", 返回 true.
给定 word = "ABCB", 返回 false.

思路

首先是不能回头，那么每次dfs将当前的位置标记（可以使用标志数组）
这里我直接将board赋值为‘ ‘，注意dfs完恢复原来的值
每一步判断越界和比较当前位置的字符是否等于word对应位置的字符
找到之后将全局flag设为true，防止做无用功

代码

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        this->board=board;
        this->word=word;
        this->mx=board.size();
        this->my=board[0].size();
        this->find=false;
        for(int i=0;i<mx;++i){
            for(int j=0;j<my;++j){
                if(dfs(i,j,0))return true;
            }
        }
        return false;
    }
private:
    bool dfs(int x,int y, int cur){
        if(cur==this->word.size()){
            this->find=true;
            return true;
        }
        if(x<0||x>=this->mx||y<0||y>=this->my||this->board[x][y]!=this->word[cur]){
            return false;
        }
        if(find){
            return true;
        }
        char tmp=board[x][y];
        board[x][y]=' ';
        if(dfs(x-1,y,cur+1)||dfs(x,y-1,cur+1)||dfs(x,y+1,cur+1)||dfs(x+1,y,cur+1)){
            find=true;
            board[x][y]=tmp;
            return true;
        }
        board[x][y]=tmp;
        return false;
    }
    vector<vector<char>>board;
    string word;
    int mx,my;
    bool find;
};

leetcode回溯算法--基础难度

原文：https://www.cnblogs.com/dionysun/p/12019692.html