数据结构与算法简记--堆和堆排序

堆

概念

• 堆是一个完全二叉树；
• 堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。
• 根据节点值跟子树的大小关系分为：大顶堆和小顶堆。

如何实现

• 如何存储
  • 二叉树章节有讲到完全二叉树适合用数组存储，所以用数组来存储堆

• 有哪些操作
  • 插入一个元素(O(logn))--插入到数组结尾，执行从下往上堆化：从下往上沿着向堆顶的路径，逐个比较，不满足就交换，满足则结束。
  • 

  • public class Heap {
      private int[] a; // 数组，从下标1开始存储数据
      private int n;  // 堆可以存储的最大数据个数
      private int count; // 堆中已经存储的数据个数
    
      public Heap(int capacity) {
        a = new int[capacity + 1];
        n = capacity;
        count = 0;
      }
    
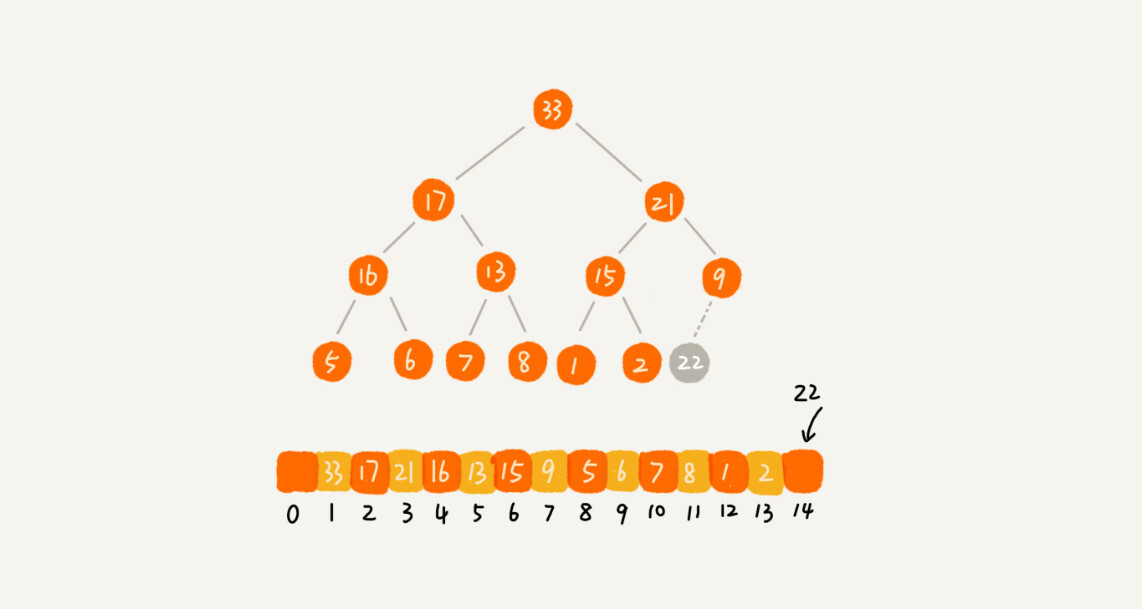
      public void insert(int data) {
        if (count >= n) return; // 堆满了
        ++count;
        a[count] = data;
        int i = count;
        while (i/2 > 0 && a[i] > a[i/2]) { // 自下往上堆化
          swap(a, i, i/2); // swap()函数作用：交换下标为i和i/2的两个元素
          i = i/2;
        }
      }
     }
    

  • 删除堆顶元素(O(logn))--我们把最后一个节点放到堆顶，然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的，互换两个节点，并且重复进行这个过程，直到父子节点之间满足大小关系为止。这就是从上往下的堆化方法。
  • 

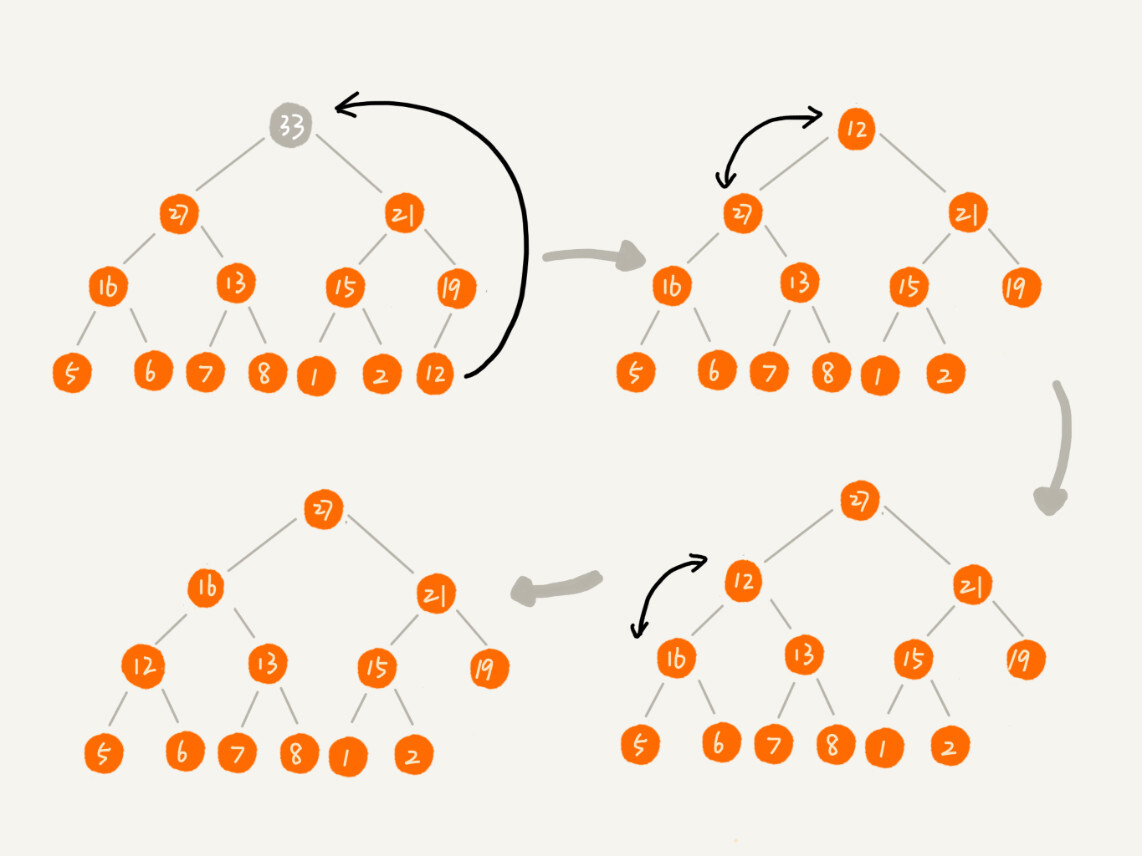
  • public void removeMax() {
      if (count == 0) return -1; // 堆中没有数据
      a[1] = a[count];
      --count;
      heapify(a, count, 1);
    }
    
    private void heapify(int[] a, int n, int i) { // 自上往下堆化
      while (true) {
        int maxPos = i;
        if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
        if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
        if (maxPos == i) break;
        swap(a, i, maxPos);
        i = maxPos;
      }
    }
    

如何基于堆实现排序？

数据结构与算法简记--堆和堆排序

原文：https://www.cnblogs.com/wod-Y/p/12032665.html