题目大意

关于这题的思路

考时思路（关于W的取值）

很显然，当选定的W越大，则Y的值也会随之减少

那么这道题便是二分查找，于是便有了二分模板，但问题来了，我们要如何缩小范围呢？

我们先看张图

case1 S≥mid

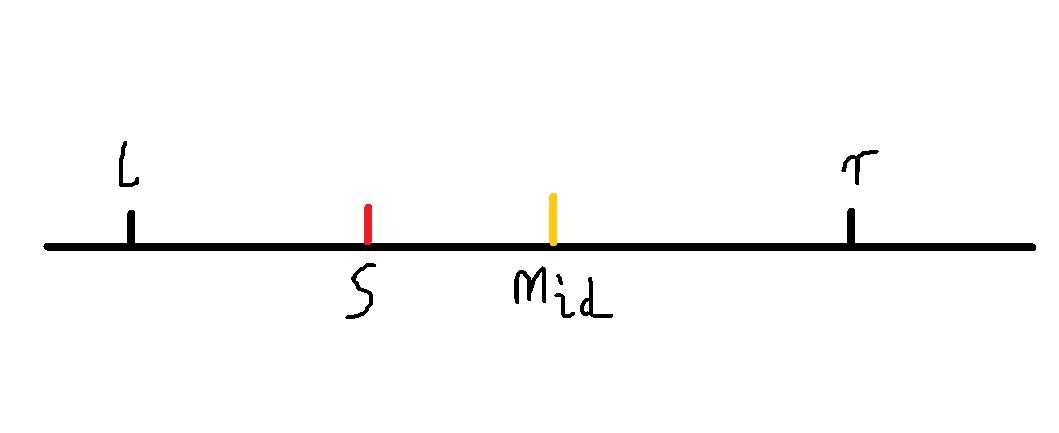
由于我们需要将mid更靠近S，所以便是让mid变大，那么更新的端点也就可想而知了

case2 S＜mid

由于我们需要将mid靠近S，所以便是另一端点更新

注意

mid的值随W增大而减小

代码+一个小优化

优化理论，W∈w[]

    while(r>=l){
        now=l+r>>1;
        k=check(W_[now]);
        ans=min(ans,abs_ull(k,S));
        if(k>S)l=now+1;
        else r=now-1;
    }

考时思路（获得W对应的值）

暴力，不说了,直接上代码

ull get(int l,int r,int W){
    int a=0,i;
    ull b=0;
    for(i=l;i<=r;i++)
    if(w[i]>=W){
        ++a;
        b=b+v[i];
    }
    return a*b;
}
ull check(int W){
    int i,j;
    ull ans=0;
    for(i=1;i<=m;i++)
    ans+=get(ll[i],rr[i],W);
    return ans;
}

考后思路（暴力的优化）

上文的暴力程序时间复杂度为n2，显然会T，有没有可以优化的方法呢？

前缀和优化 O(2n）

优化理论

对于每个l-r，我们需要求出中间的中间有多少个大于等于W的珠宝数量及其价值总和，总和就联想到前缀和

代码

for(i=1;i<=n;i++)
if(w[i]>=W){
    a[i]=a[i-1]+v[i];
    b[i]=b[i-1]+1;
}else{
    a[i]=a[i-1];
    b[i]=b[i-1];
}
for(i=1;i<=m;i++)
ans+=(a[rr[i]]-a[ll[i]-1])*(b[rr[i]]-b[ll[i]-1]);

代码解读

我们可以理解为将l-r中不符合要求的价值和数量均看做0，然后累加在a，b中

那么这一次的检阅结果就为 （a[右端点]-a[左端点-1]）*（b[右端点]-b[左端点-1]）的总和

关于这道题的总结

1.二分在具有单调性的查找中是一把利器，可以将时间复杂度从n降到㏒n

2.在一堆区间的优化方面，本质就是找出这些区间的共性，并减少共性方面的计算（也就是说只算一次），以本题为例，便是从小于W的珠宝每个区间都不符合的共性出手，进行前缀和优化

完整AC代码

#include<bits/stdc++.h>
#define ull unsigned long long
using namespace std;
int n,m;
ull S;
int W_[200010],len;
int w[200010],v[200010];
int ll[200010],rr[200010];
int a[200010],b[200010];
ull abs_ull(ull a,ull b){
    if(a>b)return a-b;
    return b-a;
}
ull check(int W){
    ull ans=0;
    a[0]=b[0]=0;
    int i,j;
    for(i=1;i<=n;i++)
    if(w[i]>=W){
        a[i]=a[i-1]+v[i];
        b[i]=b[i-1]+1;
    }else{
        a[i]=a[i-1];
        b[i]=b[i-1];
    }
    for(i=1;i<=m;i++)
    ans+=(a[rr[i]]-a[ll[i]-1])*(b[rr[i]]-b[ll[i]-1]);
    return ans;
}
ull min(ull AA,ull BB){
    return AA>BB?BB:AA;
}
int main( ){
    std::ios::sync_with_stdio(false);
    cin>>n>>m>>S;
    int i,j;
    for(i=1;i<=n;i++){
        cin>>w[i]>>v[i];
        W_[++len]=w[i];
    }
    sort(W_+1,W_+len+1);
    ull ans=200000000000;
    for(i=1;i<=m;i++)
    cin>>ll[i]>>rr[i];
    int now;
    int l=1,r=len;
    ull k;
    while(r>=l){
        now=l+r>>1;
        k=check(W_[now]);
        ans=min(ans,abs_ull(k,S));
        if(k>S)l=now+1;
        else r=now-1;
    }
    cout<<ans<<endl;
}

P1314 聪明的质监员

原文：https://www.cnblogs.com/the-Blog-of-Mikasa/p/12038537.html