首页 > 编程语言 > 详细

BZOJ-1002&洛谷P2144【FJOI2007】轮状病毒--py+Java+c++写法（生成树计数-矩阵树-基尔霍夫矩阵-高精度）

时间：2019-12-15 17:02:46      阅读：79      评论：0      收藏：0      [点我收藏+]

题目链接：https://www.lydsy.com/JudgeOnline/problem.php?id=1002

洛谷：

时间限制1.00s
内存限制125.00MB
 
BZOJ: Time Limit: 1 Sec  Memory Limit: 162 MB
 

Description

　　轮状病毒有很多变种，所有轮状病毒的变种都是从一个轮状基产生的。一个N轮状基由圆环上N个不同的基原子
和圆心处一个核原子构成的，2个原子之间的边表示这2个原子之间的信息通道。如下图所示

技术分享图片

　　N轮状病毒的产生规律是在一个N轮状基中删去若干条边，使得各原子之间有唯一的信息通道，例如共有16个不
同的3轮状病毒，如下图所示

技术分享图片
　　现给定n(N<=100)，编程计算有多少个不同的n轮状病毒

 

Input

　　第一行有1个正整数n

Output

　　计算出的不同的n轮状病毒数输出

Sample Input

3

Sample Output

16
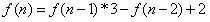
其实这道题很简单。。。先给出递推式：技术分享图片

 然后我们py一发：

n=int(input())
f=[]
f.append(1)
f.append(5)
for i in range(2,n):
    p=f[i-1]*3-f[i-2]+2
    f.append(p)
print(f[n-1])

A了。。。

大整数嘛，Java同样也挺好用的：

import java.math.BigInteger;
import java.util.Scanner;

class Main {
    public static void main(String[] args){
        BigInteger a[]=new BigInteger[120];
        Scanner sc=new Scanner(System.in);
        a[1]=new BigInteger("1");
        a[2]=new BigInteger("5");
        int n=sc.nextInt();
        for (int i=3; i<=n; i++){
            a[i]=a[i-1].multiply(new BigInteger("3")).subtract(a[i-2]).add(new BigInteger("2"));
        }
        System.out.println(a[n]);
    }
}

 

想想还是不能这样。。。我们要知道为什么是这样的，1.打表，2.矩阵树

打表就算了，矩阵树是计算一个图的生成树的个数的，它是由基尔霍夫矩阵的n-1阶行列式的绝对值得到的，其具体计算过程如下：

D(i,j)代表第i个点的度，其实只有主对角线有值，E(i,j)代表第i个点到第j个点有边，其中i-i不算，也就是说主对角线全为零，我们可以来试一下本题：

技术分享图片

这个矩阵解出来不难，化为上三角矩阵，做出它的行列式，最后会发现有一行全为0，对角线相乘（剔除0）为16。

那么当这个3扩大到n的时候这个基尔霍夫矩阵长什么样子呢？可以想到的是，主对角线除了第一行第一列为n，其他的全是3，第一行和第一列的其他元素全为-1，其他主对角线3的两侧有-1，当然，第二列的最后一行和最后一列的第二行也有-1，毕竟首尾跨区域了嘛：

技术分享图片

 那么我们现在有两种方法解决这题，一是手动求解，算出递推式，相信高等代数或线性代数学得好的不难求出，然后就是简单的要么py，要么Java来一发，C/C++也可以，只不过比较麻烦，需要大整数。

手动求解：

由于是n-1阶子式，所以我们把第一行第一列扔掉是比较容易算的，那么就剩下了主对角线为3，每个3的上下都有一个-1，第一列最下面有个-1，最后一列最上面有个-1。

然后我们展开就会得到3个子矩阵。。。。balbalbal

第二种方法就是让计算机求解：

利用高斯消元，O（N3）的复杂度，n只有100，可以忍受。

听起来高斯消元有点高大上，其实就是个矩阵化为上三角的过程，模拟一下就OK了，每一行减去初始行，慢慢搞：

高斯消元打表过程：

技术分享图片 
#include <bits/stdc++.h>
using namespace std;

#define clc(x) memset(x,0,sizeof x);

const int mac=110;

int d[mac][mac],eg[mac][mac];
double huf[mac][mac];

inline void debug_huf(int n)
{
    for (int i=1; i<=n; i++)
        for (int j=1; j<=n; j++)
            printf("%.3f%c",huf[i][j],j==n?‘\n‘:‘ ‘);
}

int main()
{
    freopen("in.txt","r",stdin);
    int n;
    while (~scanf("%d",&n)){
        if (n==1 || n==2) {
            if (n==2) printf ("5\n");
            else printf ("%d\n",1);
            continue;
        }
        n++;
        clc(eg);clc(huf);clc(d);
        for (int i=1; i<=n; i++)
            if (i==1) d[i][i]=n-1;
            else d[i][i]=3;
        for (int i=2; i<=n; i++) eg[i][1]=1,eg[1][i]=1;
        for (int i=2; i<=n; i++) 
            eg[i][i-1]=1,eg[i][i+1]=1,eg[i-1][i]=1,eg[i+1][i];
        eg[2][n]=1;eg[n][2]=1;
        for (int i=2; i<=n; i++)
            for (int j=2; j<=n; j++)
                huf[i-1][j-1]=d[i][j]-eg[i][j];
        n--;
        for (int i=1; i<n; i++){//第j行-第i行
            for (int j=i+1; j<=n; j++){//第j行的第k个元素改变
                double p=huf[j][i]/huf[i][i];
                huf[j][i]=0;
                for (int k=i+1; k<=n; k++){
                    huf[j][k]-=huf[i][k]*p;
                }
            }
        }
        //debug_huf(n);
        double ans=1;
        for (int i=1; i<=n; i++) ans*=fabs(huf[i][i]);
        printf("%.0f\n",ans);
    }
    return 0;
}
View Code

将前10项打出来就是：

1
5
16
45
121
320
841
2205
5776
15125

 然后利用多元线性关系求出递推关系，就是for几遍，看看能不能找到一个递推关系符合前10项，最后得到3 -1 2。。。。

我们可以用这个double的范围交一发在洛谷上，看看能过几个测试点，：

技术分享图片

然后想想，我们还有个long double的骚操作，我们改用long double交一发。。一样的结果，看来这些没过的数据确实比较大

这也是打表。。。是在我们不想写大整数的情况下找到递推式，然后py一发，或者Java一发，如果用py或者Java写高斯消元的话可能会T，特别是Java，递推写法100ms左右，也就是我们只循环了100遍就100ms了，所以Java大概率会T掉。

当然这里也给出py，Java，C++的本题大整数高斯消元过程：

 py写法：

技术分享图片 
n=int(input())
d=[]
eg=[]
huf=[]
for i in range(n+10):
    d.append([])
    eg.append([])
    huf.append([])
    for j in range(n+10):
        d[i].append(0)
        eg[i].append(0)
        huf[i].append(0)
if n==1:
    print(1)
elif n==2:
    print(5)
else :
    n=n+1
    d[1][1]=n-1
    for i in range(2,n+1):
        d[i][i]=3
    for i in range(2,n+1):
        eg[i][1]=eg[1][i]=1
    for i in range(2,n+1):
        eg[i][i-1]=eg[i+1][i]=eg[i-1][i]=eg[i+1][i]=1
    eg[2][n]=eg[n][2]=1
    for i in range(2,n+1):
        for j in range(2,n+1):
            huf[i-1][j-1]=d[i][j]-eg[i][j]
    n=n-1
    for i in range(1,n):
        for j in range(i+1,n+1):
            p=huf[j][i]/huf[i][i]
            huf[j][i]=0
            for k in range(i+1,n+1):
                huf[j][k]-=huf[i][k]*p
    ans=1
    for i in range(1,n+1):
        ans*=abs(huf[i][i])
    print(‘%.0f‘% ans)
View Code

如何你会发现和之前的double交的测试结果一样。。。和之前py写的递推过程对拍一下发现越到后面会出现越大的误差。。。

所以真正的高斯消元并不是用浮点数运算的，而是通过更相减损术（辗转相除）实现的！！注意矩阵的行与行之间互换并不影响其行列式的绝对值。

所以最终AC的py代码：

技术分享图片 
n=int(input())
d=[]
eg=[]
huf=[]
f=[]
for i in range(n+10):
    d.append([])
    eg.append([])
    huf.append([])
    f.append(0)
    for j in range(n+10):
        d[i].append(0)
        eg[i].append(0)
        huf[i].append(0)
if n==1:
    print(1)
elif n==2:
    print(5)
else :
    n=n+1
    d[1][1]=n-1
    for i in range(2,n+1):
        d[i][i]=3
    for i in range(2,n+1):
        eg[i][1]=eg[1][i]=1
    for i in range(2,n+1):
        eg[i][i-1]=eg[i+1][i]=eg[i-1][i]=eg[i+1][i]=1
    eg[2][n]=eg[n][2]=1
    for i in range(2,n+1):
        for j in range(2,n+1):
            huf[i-1][j-1]=d[i][j]-eg[i][j]
    n=n-1
    ans=1
    for i in range(1,n+1):
        for j in range(i+1,n+1):
            while huf[j][i] :
                p=huf[i][i]//huf[j][i]
                for k in range(i,n+1):
                    huf[i][k]-=huf[j][k]*p
                huf[i],huf[j]=huf[j],huf[i]
                ans=-ans
        ans*=huf[i][i]
    print(ans)
View Code

Java的话就不写D矩阵和E矩阵了，不然会很麻烦，反正最终矩阵我们是知道的，所以直接上手就好了，居然没T掉。。。神奇，看来Java有个基础时间，运行速度倒不是很慢。以下是Java的AC代码：

技术分享图片 
import java.math.BigInteger;
import java.util.Scanner;

class Main {
    public static void main(String[] args){
        BigInteger huf[][]=new BigInteger[120][120];
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        if (n==1) System.out.println("1");
        else if (n==2) System.out.println("5");
        else {
            for (int i=0; i<=n; i++)
                for (int j=0; j<=n; j++)
                    huf[i][j]=new BigInteger("0");
            for (int i=1; i<=n; i++){
                huf[i][i]=new BigInteger("3");
                huf[i][i-1]=huf[i-1][i]=huf[i][i+1]=huf[i+1][i]=new BigInteger("-1");
            }
            huf[1][n]=huf[n][1]=new BigInteger("-1");
            BigInteger ans=new BigInteger("1");
            for (int i=1; i<=n; i++){
                for (int j=i+1; j<=n; j++){
                    while (!huf[j][i].equals(new BigInteger("0"))){
                        BigInteger p=huf[i][i].divide(huf[j][i]);
                        for (int k=i; k<=n; k++){
                            huf[i][k]=huf[i][k].subtract(huf[j][k].multiply(p));
                            BigInteger tmp=huf[i][k];
                            huf[i][k]=huf[j][k];
                            huf[j][k]=tmp;
                        }
                        ans=ans.multiply(new BigInteger("-1"));
                    }
                }
                ans=ans.multiply(huf[i][i]);
            }
            System.out.println(ans);
        }
    }
}
View Code

接下来就是最难搞的C/C++了。。。不过没办法，以后肯定会遭遇C/C++大整数的，我们这里手写，不用板子（板子太长了，比赛的时候肯定不能用，所以练习一下手敲）：

 。。。C++写的。。。矩阵也需要开大整数，然后我觉得直接丢公式吧QAQ，然后就是挺简单的高精度乘低精度，然后高精度直接的减法，当然高精度减法要考虑正负和前导零的，但本题并不会出现这种情况，所以就可以直接愉快的写了：

#include <bits/stdc++.h>
using namespace std;

const int mac=200;
const int mod=10;

vector<int>ans[mac];

vector<int> mult(vector<int> a,int b)
{
    int len=a.size();
    for (int i=0; i<len; i++)
        a[i]*=b;
    for (int i=0; i<len; i++){
        if (a[i]>=mod){
            int p=a[i]/mod;
            if (i+1==len){
                a[i]-=p*mod;
                a.push_back(p);
            }
            else {
                a[i]-=p*mod;
                a[i+1]+=p;
            }
        }
    }
    return a;
}

vector<int> subct(vector<int>a,vector<int>b)
{
    int lena=a.size(),lenb=b.size();
    for (int i=0; i<min(lena,lenb); i++){
        a[i]-=b[i];
    }
    for (int i=0; i<lena; i++){
        while (a[i]<0) a[i]+=10,a[i+1]-=1;
    }
    return a;
}

vector<int> add(vector<int>a,int b)
{
    a[0]+=b;
    int i=0; 
    while (a[i]>=10){
        a[i]-=10;a[i+1]++;
        i++;
    }
    return a;
}

void out(vector<int>v)
{
    int len=v.size();
    for (int i=len-1; i>=0; i--)
        printf("%d",v[i]);
    printf("\n");
}

int main()
{
    //freopen("in.txt","r",stdin);
    int n;
    scanf ("%d",&n);
    ans[1].push_back(1);
    ans[2].push_back(5);
    for (int i=3; i<=n; i++){
        vector<int>p=mult(ans[i-1],3);
        ans[i]=subct(p,ans[i-2]);
        ans[i]=add(ans[i],2);
    }
    out(ans[n]);
    return 0;
}

 

 

 

BZOJ-1002&洛谷P2144【FJOI2007】轮状病毒--py+Java+c++写法（生成树计数-矩阵树-基尔霍夫矩阵-高精度）

原文：https://www.cnblogs.com/lonely-wind-/p/12037948.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
分享档案
更多>
2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)
最新文章
更多>
教程昨日排行
更多>
友情链接
汇智网   PHP教程   插件网  
关于我们 - 联系我们 - 留言反馈 - 联系我们:wmxa8@hotmail.com
© 2014 bubuko.com 版权所有
打开技术之扣，分享程序人生！