如何实现一个基本的计算系统?
已知的基本事实:
加减乘除运算都可以转换为加减法运算来实现
加减法运算又可以转化为逻辑运算来实现
为了让外界操纵这些基本动作与或非, 我们就需要一些指令, 通过这些指令就可以调用这些基本动作, 指令: 控制基本动作的命令, 当我们有了指令, 就可以通过组合, 就可以实现一些复制的动作, 这些组合就可以看做是程序.
拆解程序中的复制动作--> 基本动作 , 这就是程序执行机构
执行机构, 自动解释程序中的各种组合, 并按照次序调用指令, 实现基本动作, 并予以执行
所以:
基本动作---> 程序 ----> 程序执行机构就构成了一个基本的计算机系统
在将低层次的抽象为更高层次的计算机结构
我们执行了 2+3 ---->程序编译系统 ----> 低层次的计算机系统(异或) ---> 机器指令0-1 ---> 执行
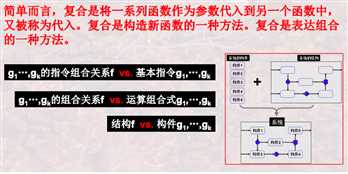
运算组合式通过嵌套来实现复杂的计算过程
(+ 2 4) (-6 3)
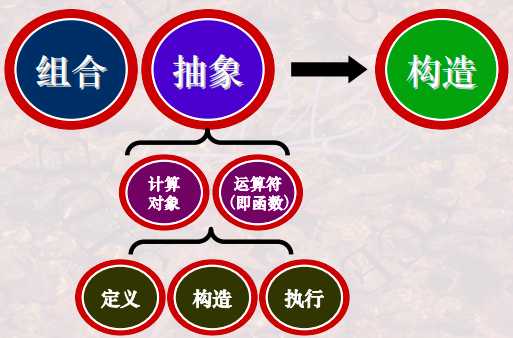
组合越来越复杂的时候, 可以通过抽象, 将复杂的式子命名为一个名字, 这样在计算中就可以使用名字来进行计算对象来替换名字
define height 2
height 2
define pi 3.14
define redius 10










原文:https://www.cnblogs.com/jly1/p/12046643.html