定义
1 所谓的一棵二分查找树(Binary search tree) T,要么是一棵空树,要么是以 r = (key, value) 为根节点的二叉树,而且其左、右子树都是二分查找树,同时 n 在 r 的左子树中,所有节点(如果存在的话)的关键码均不大于 key; o 在 r 的右子树中,所有节点(如果存在的话)的关键码均不小于 key。
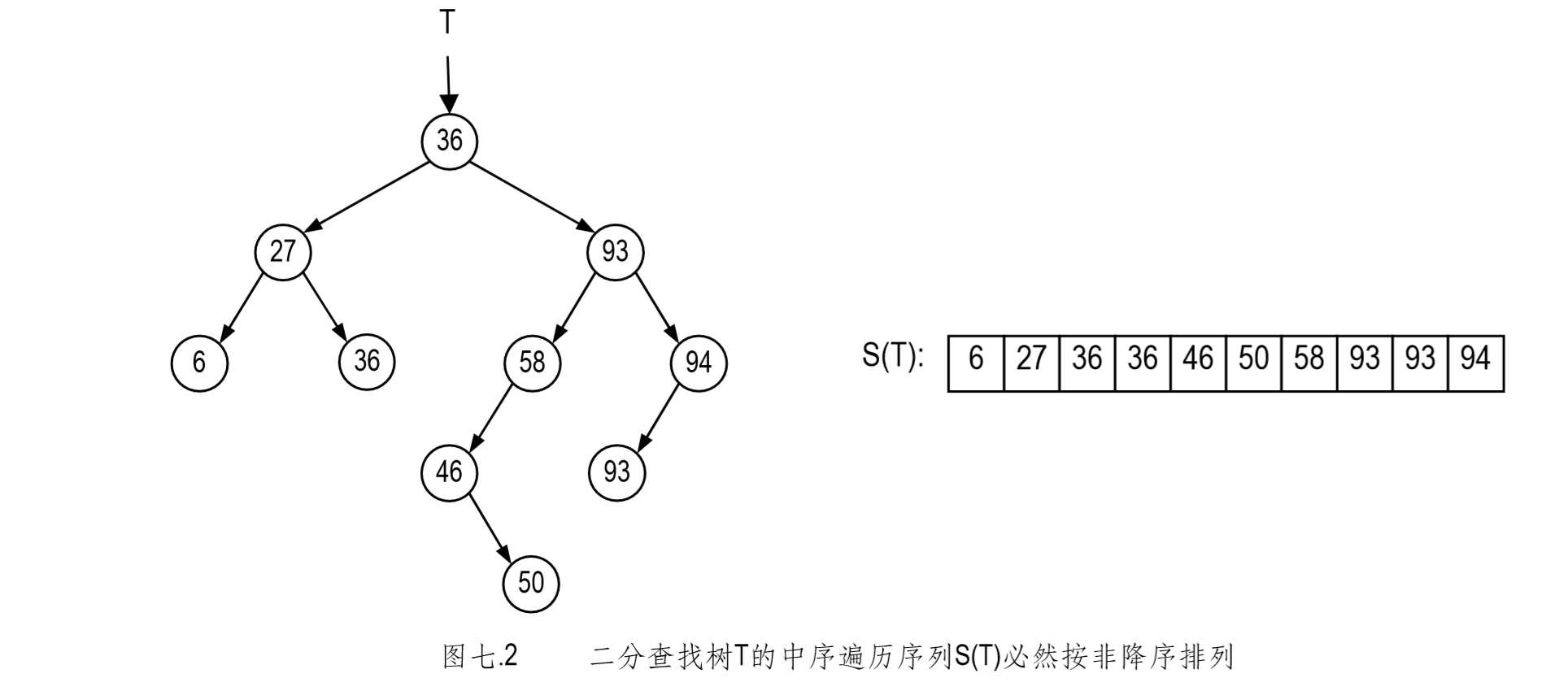
二叉树 T 为二分查找树,当且仅当其中序遍历序列是单调非降的。
查找算法
二分查找树查找算法的构思是:从根节点始,以递归的形式不断缩小查找范围,直到发现目 标条目(查找成功)或查找范围缩小至空树(查找失败)。
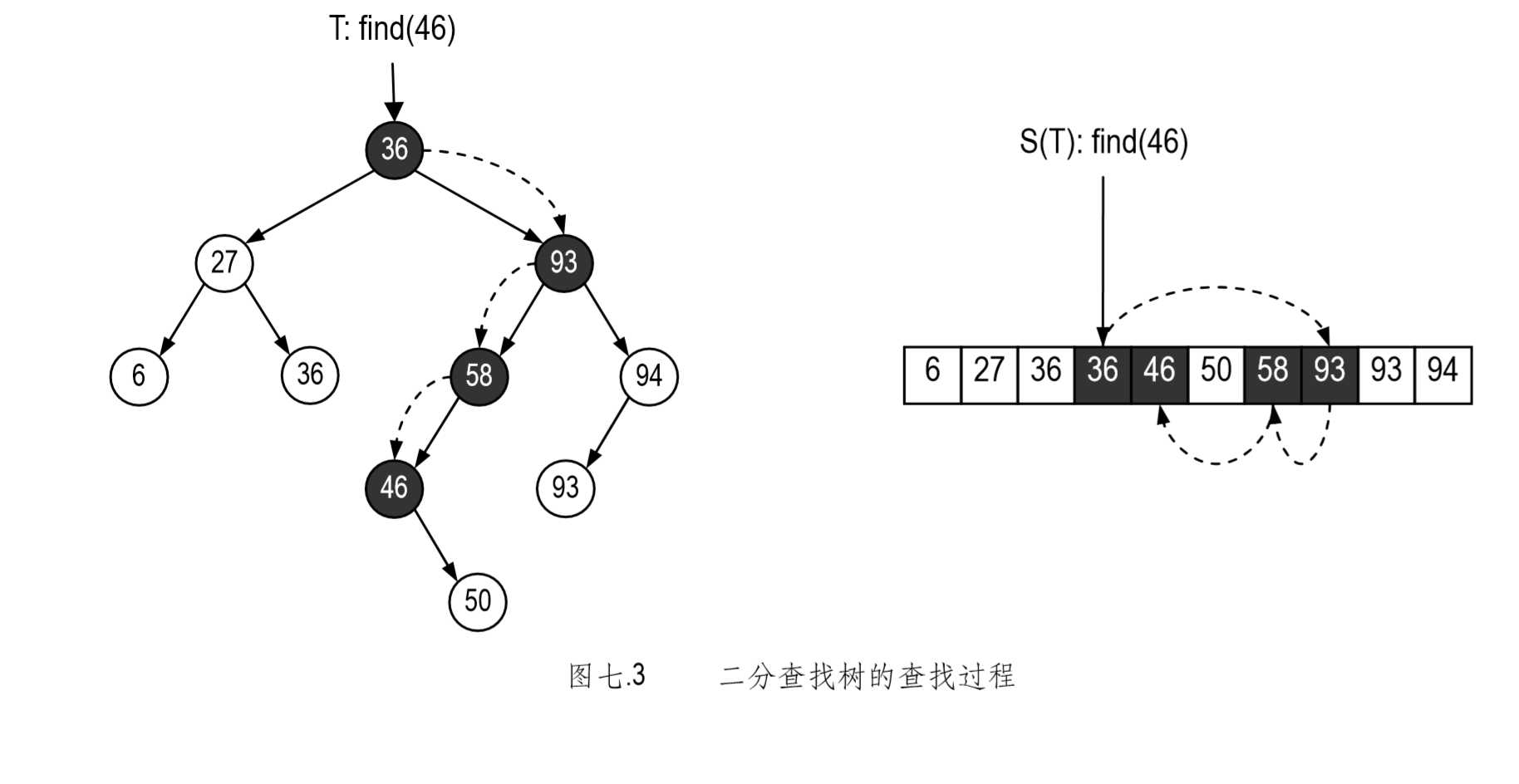
在递归的每一层,一旦发现当前节点为 null,则说明查找范围已经为空,查找失败;否则,我 们将目标关键码与当前节点的关键码做对比。与有序查找表的二分查找过程类似,这里的比较结果 也不外乎三种可能:
1. 目标关键码更大(比如在节点 36 处)。此时,可以深入右子树中做递归查找;
2. 目标关键码更小(比如在节点 93 和 58 处)。此时,可以深入左子树中做递归查找;
3. 相等(比如在节点 46 处)。此时算法以“查找成功”结束。
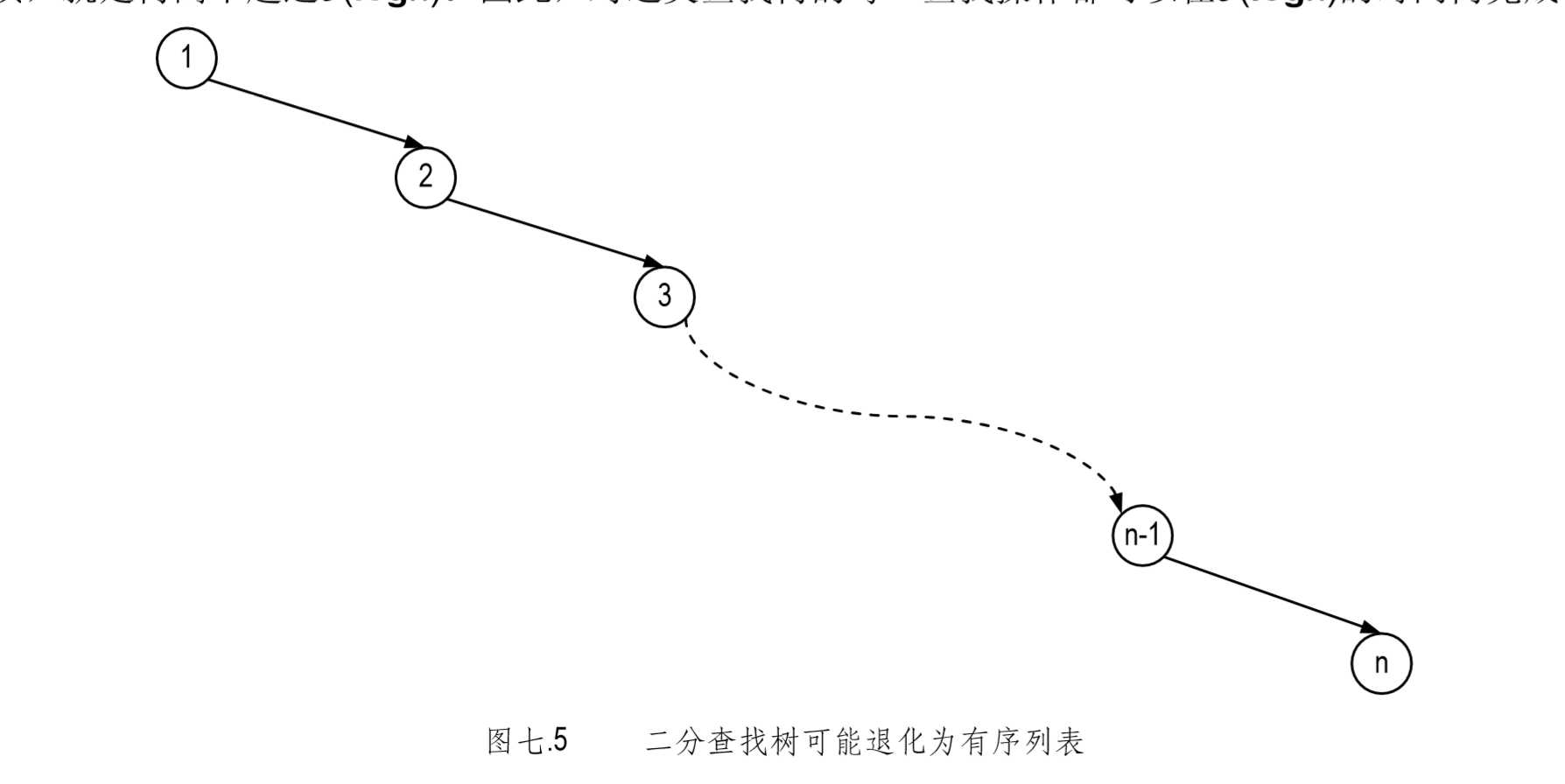
,一般的二分查找树对其高度没有任何限制,在坏情况下,由n个节点构成的二分查找 树的高度可以达到Θ(n)。如 图七.5 所示,当所有节点都没有左孩子时,就是这样的一种极端情况。 此时,查找操作在坏情况下可能需要线性的时间??这并不奇怪,因为实际上,这样的一棵“二 分”查找树已经退化为了一个不折不扣的有序查找表。
查找算法

插入算法

删除算法

对于节点有两个孩子?我们删除的时候只要记住一点,二叉树有个中序排列的树,我们删除的节点要找下一个min(大于这个节点值的节点)。
https://blog.csdn.net/isea533/article/details/80345507这篇blog的图还是不错的,我们要掌握一种思维,所以并不需要看原博主写的代码。我已经列出伪代码了。
原文:https://www.cnblogs.com/CherryTab/p/12056755.html