Taylor级数（对函数进行高阶逼近）： 对复杂函数使用多项式
进行逼近
****************************************************************************************
泰勒公式告诉我们，怎么把铁丝弯成不同的样子
泰勒公式一句话描述：就是用多项式函数去逼近光滑函数。
先来感受一下：
设nn是一个正整数。如果定义在一个包含aa的区间上的函数ff在aa点处n+1n+1次可导，那么对于这个区间上的任意x都有：
，其中的多项式称为函数在aa处的泰勒展开式，Rn(x)Rn(x)是泰勒公式的余项且是(x−a)n(x−a)n的高阶无穷小。----维基百科
泰勒公式的定义看起来气势磅礴，高端大气。如果 的话，就是麦克劳伦公式，即：
，这个看起来简单一点，我们下面只讨论麦克劳伦公式，可以认为和泰勒公式等价。
1.多项式的函数图像特点
展开来就是 
，
这些都是常数，我们暂时不管，先看看其中最基础的组成部分，幂函数有什么特点。
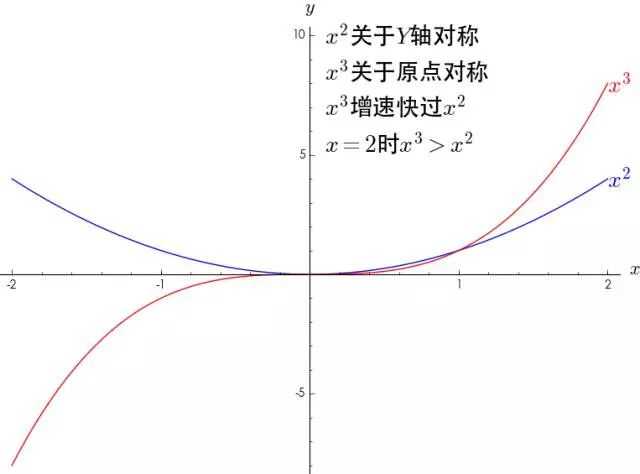
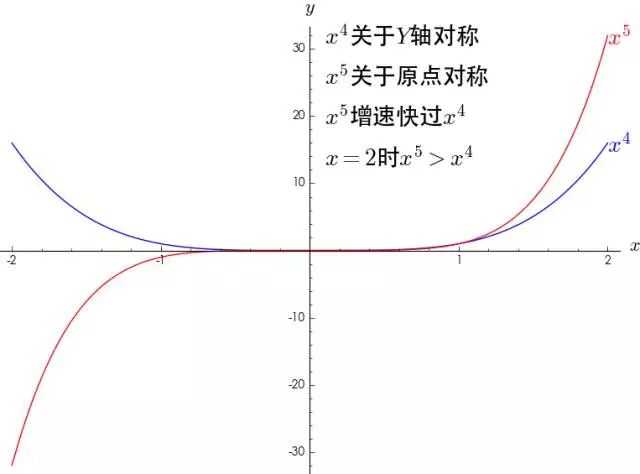
可以看到，幂函数其实只有两种形态，一种是关于 轴对称，一种是关于原点对称，并且指数越大，增长速度越大。
那幂函数组成的多项式函数有什么特点呢？
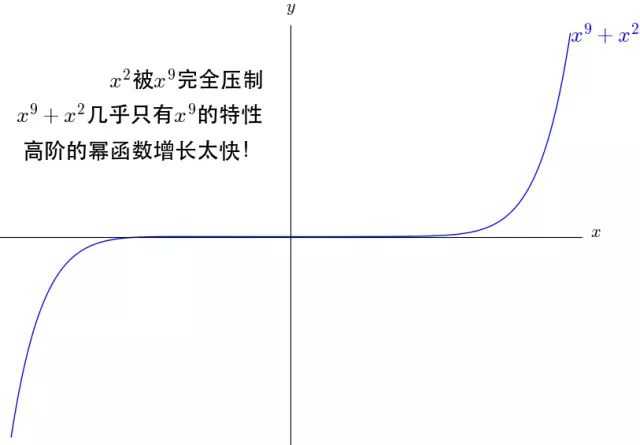
怎么才能让 和
的图像特性能结合起来呢？
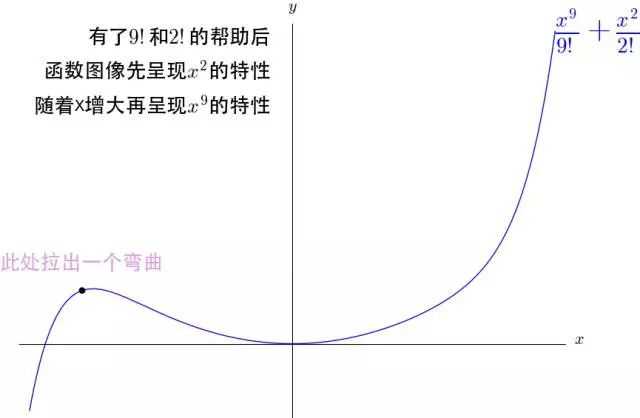
我们来动手试试看看系数之间如何压制的：
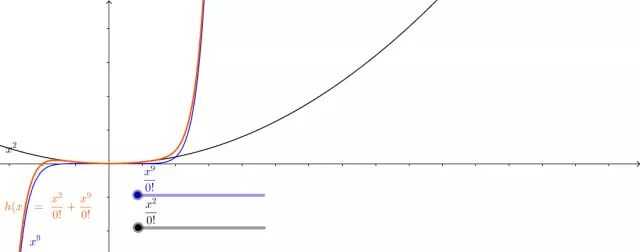
通过改变系数，多项式可以像铁丝一样弯成任意的函数曲线。送你一颗心（虽然是隐函数，意思一下）：
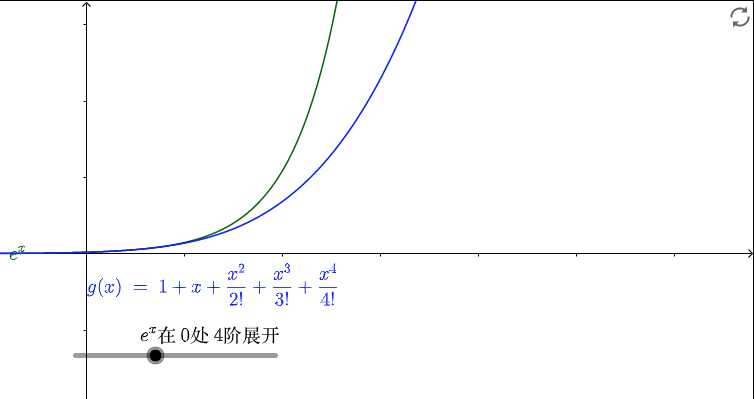
2.用多项式对 
进行逼近：
是麦克劳伦展开形式上最简单的函数，有
就是这么任性。
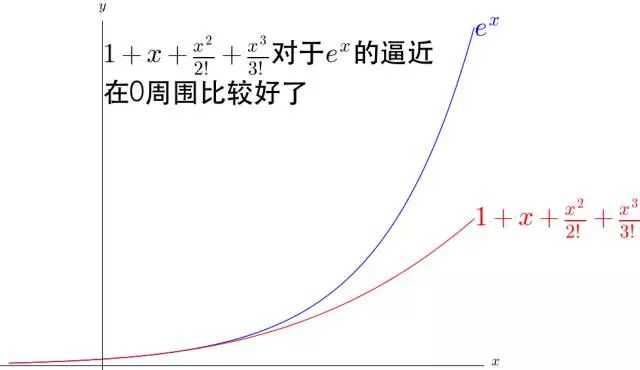
增加一个 看看。
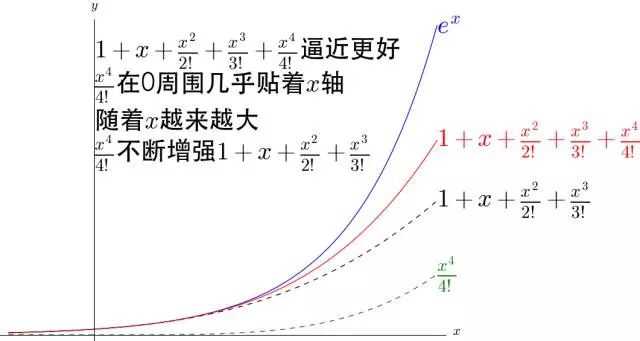
增加一个 看看。
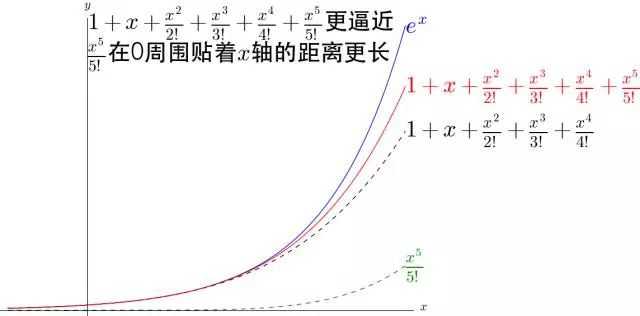
可以看出， 不断的弯曲着那根多项式形成的铁丝去逼近
。并且
越大，起作用的区域距离0越远。
3.用多项式对 
进行逼近
是周期函数，有非常多的弯曲，难以想象可以用多项式进行逼近。
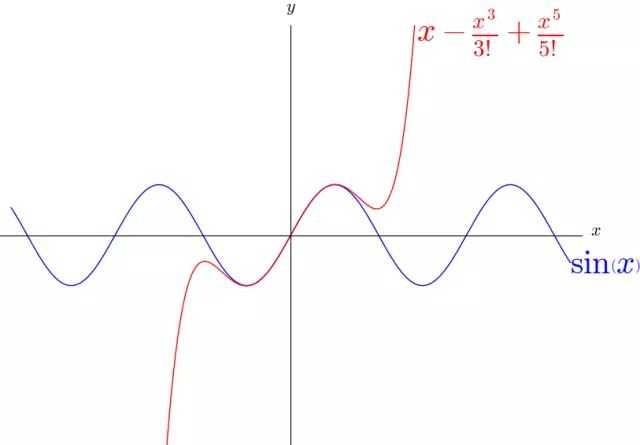
同样的，我们再增加一个 试试。
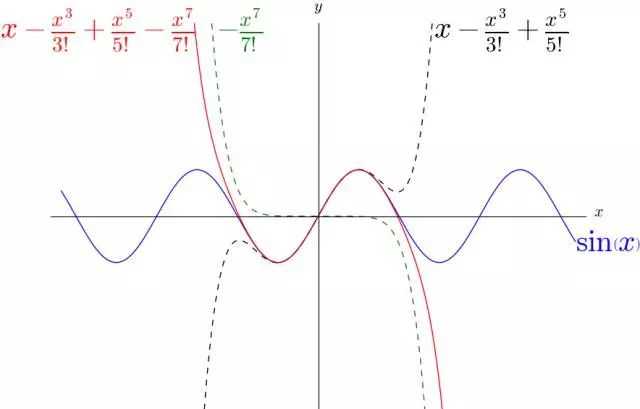
可以看到 在适当的位置，改变了
的弯曲方向，最终让
更好的逼近了
。
一图胜前言，动手看看 的展开吧：
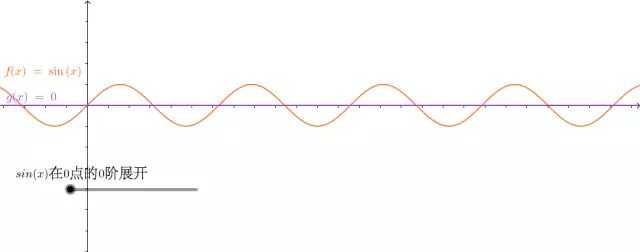
4.泰勒公式与拉格朗日中值定理的关系
拉格朗日中值定理：如果函数 满足，在
上连续，在
上可导，那么至少有一点
(
)使等式
成立。
数学定义的文字描述总是非常严格、拗口，我们来看下拉格朗日中值定理的几何意义：
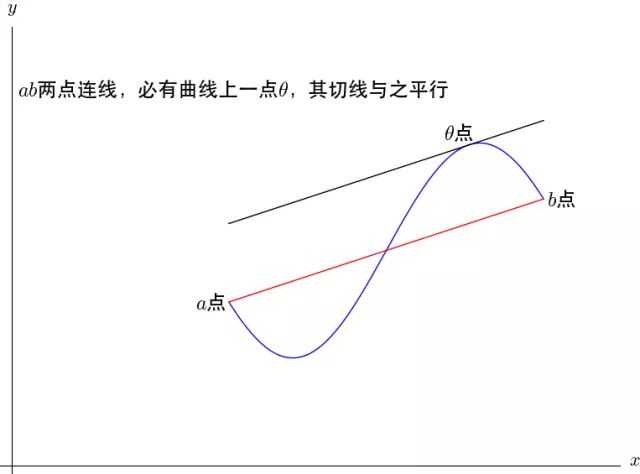
这个和泰勒公式有什么关系？泰勒公式有个余项 我们一直没有提。
余项即使用泰勒公式估算的误差，即:
余项的代数式是， ，其中
。是不是看着有点像了？
当 的时候，根据泰勒公式有，
，把拉格朗日中值定理中的
换成
，那么拉格朗日中值定理根本就是
时的泰勒公式。
结合拉格朗日中值定理，我们来看看 的时候，泰勒公式的几何意义：
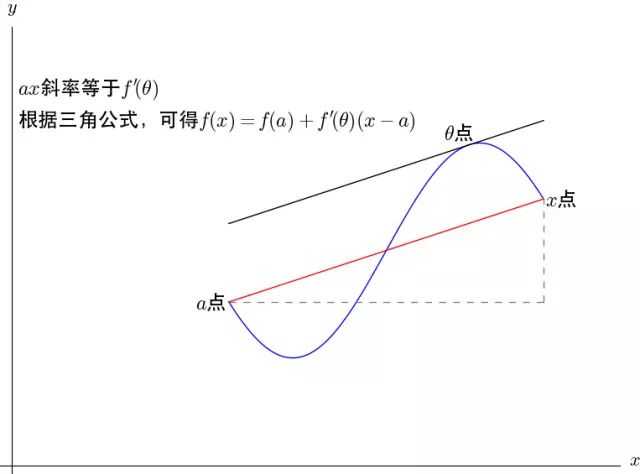
当 的时候，泰勒公式几何意义很好理解，那么
呢？
这个问题我是这么理解的：首先让我们去想象高阶导数的几何意义，一阶是斜率，二阶是曲率，三阶四阶已经没有明显的几何意义了，或许，高阶导数的几何意义不是在三维空间里面呈现的，穿过更高维的时空才能俯视它的含义。现在的我们只是通过代数证明，发现了高维投射到我们平面上的秘密。
还可以这么来思考泰勒公式，泰勒公式让我们可以通过一个点来窥视整个函数的发展，为什么呢？因为点的发展趋势蕴含在导数之中，而导数的发展趋势蕴含在二阶导数之中......四不四很有道理啊？
5.泰勒公式是怎么推导的？
很多同学看到这段时，可能有点看不懂，我在牛顿插值的几何解释是怎么样的？ - 知乎，这个回答里尝试重新作答了。
根据“以直代曲、化整为零”的数学思想，产生了泰勒公式。
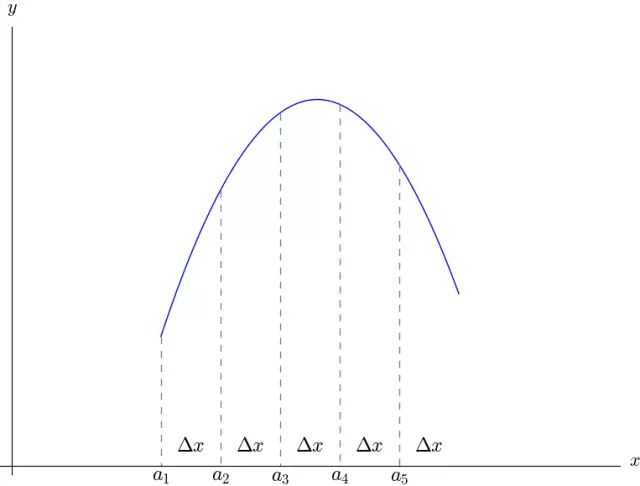
如上图，把曲线等分为 份，分别为
，
，
，
，令
，
， ，
。我们可以推出（
，
可以认为是二阶、三阶微分，其准确的数学用语是差分，和微分相比，一个是有限量，一个是极限量）：
也就是说，f(x)全部可以由 和
决定，这个就是泰勒公式提出的基本思想。据此的思想，加上极限
，就可以推出泰勒公式。
6.泰勒公式的用处
多项式这种函数是我们可以亲近的函数，它们很开放、很坦白，心里想什么就说什么，比如 ：
，这个多项式会告诉我们想问的任何消息，甚至更多，譬如，我们问：“嘿，老兄，你在4那点的值是多少？”这时
会毫不犹豫的回答：“你把4代进来，就会得到
，顺便告诉你，我最近长了奇怪的疹子，痒的要命，还好这两天症状减轻了...”。但是
阴暗、多疑，要是问它：“嗨，你在3的值是多少啊？”你得到的答案可能是：“你要干什么？为什么打听别人的私事？你以为凭着你那点加减乘除的三脚猫功夫就可以查出我的底细？况且我在3的值是多少，干你什么事！”----《微积分之倚天宝剑》
泰勒公式最直接的一个应用就是用于计算，计算机一般都是把 进行泰勒展开进行计算的。
泰勒公式还可以把问题简化，比如计算， ，代入
的泰勒展开有：
，其中
是泰勒公式里面的余项，是高阶无穷小，
。解题神器有没有？
文章最新版本在（有可能会有后续更新）：如何通俗地解释泰勒公式？