[CodeForces - 1272D] Remove One Element 【线性dp】

标签：题解 codeforces题解

题目描述

Time limit
2000 ms
Memory limit
262144 kB
Source
Codeforces Round #605 (Div. 3)
Tags
brute force ? dp ? *1500
Site
https://codeforces.com/problemset/problem/1272/D

题面

Example
Input1

5
1 2 5 3 4

Output1

4

Input2

2
1 2

Output2

2

Input3

7
6 5 4 3 2 4 3

Output3

2

题目大意

给定一个序列\(a[1 \cdots n]\)，可以删掉其中的任意一个数（当然也可以选择不删），问这其中最长的连续的严格递增序列的长度是多少？

例如，
给定\(n = 5, \;a[1 \cdots 5] = \text{{1, 2, 5, 3, 4}}\).

如果我们不删除数的话，最长的连续严格递增序列分别为\(\text{{1, 2}}\) 和 \(\text{{3, 4}}\), 长度为2。
如果我们删掉\(a[3] = 5\)，最长的连续严格递增序列为\(\text{{1, 2, 3, 4}}\)，长度为4。
如果我们删掉其他的数的话，最长的连续严格递增序列长度还是2。
所以最终答案为4，输出4。

解析

天宇给我看这道题的时候就告诉我是一道dp题了，所以一开始就按照dp的思路莽了。

简单的线性dp问题。

• 首先我们考虑不删除数，找到序列内最长连续严格递增序列的长度如何解决。
  
  设\(dp[i][0]\)为到第\(i\)个数为止，且包含第\(i\)个数的连续严格递增序列的长度。
  初始化\(dp[1 \cdots n][0] = 1\)，因为自己一定是自己所在的严格递增序列的其中的一个元素。
  状态转移方程 \[dp[i][0] = dp[i - 1][0] + 1 \,\,(if\;\; a[i] > a[i - 1])\]

• 之后我们加入删除一个数的操作。
  
  想要删除一个数，只有在前两个数比当前这个数小的时候（即 \(a[i] > a[i - 2]\)）才有必要。
  
  设\(dp[i][1]\)为到第\(i\)个数为止，且包含第\(i\)个数的，且在其中任意一个位置删除了一个数或没有删除数的连续严格递增序列长度（也可以理解为到这个位置为止包含它自身的最长连续严格递增序列的长度）。
  初始化\(dp[i][1] = dp[i][0] = 1\)。
  状态转移方程 \[dp[i][1] = \begin{cases} \max{(dp[i][1], dp[i - 1][1] + 1)}, & if \; a[i] > a[i -1]\\[2ex] \max{(dp[i][1], dp[i - 2][0] + 1)}, & if\; a[i] > a[i - 2] \end{cases}\]
  想要删除一个数，需要拿之前没有删除过数的状态\(dp[i - 2][0]\)更新，所以我们也要维护\(dp[1 \cdots n][0]\)序列。
  当\(a[i] > a[i - 2]\)时，可能会出现没必要删除\(a[i - 1]\)的情况\((a[i] > a[i - 1]> a[i - 2])\)，所以要比较一下\(dp[i][1]\)与\(dp[i - 2][0] + 1\)的大小。

• 因为每一个\(dp[i][1]\)是当前\(a[i]\)所在连续严格递增序列的长度，所以想要知道最长的长度，需要最后再扫一遍\(dp[i][1]\)找到最大值。

通过代码

/*
Status
    Accepted
Time
    46ms
Memory
    2364kB
Length
    944
Lang
    GNU G++11 5.1.0
Submitted
    2019-12-18 09:35:42
RemoteRunId
    67132818
*/

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 2e5 + 50;

int a[MAXN], dp[MAXN][2];

inline int read()      //快读，2e5的输入量，加入快读能明显加快程序运行速度.
{
    int res = 0, f = 1;
    char ch;

    ch = getchar();

    while(!isdigit(ch)){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(isdigit(ch)){
        res = (res << 3) + (res << 1) + ch - 48;
        ch = getchar();
    }

    return f * res;
}
int main()
{
    int n;

    n = read();

    for(int i = 1; i <= n; i ++){     //读入加dp数组的初始化.
        a[i] = read();
        dp[i][0] = 1;
        dp[i][1] = 1;
    }

    for(int i = 2; i <= n; i ++){      //状态转移.
        if(a[i] > a[i - 1]){
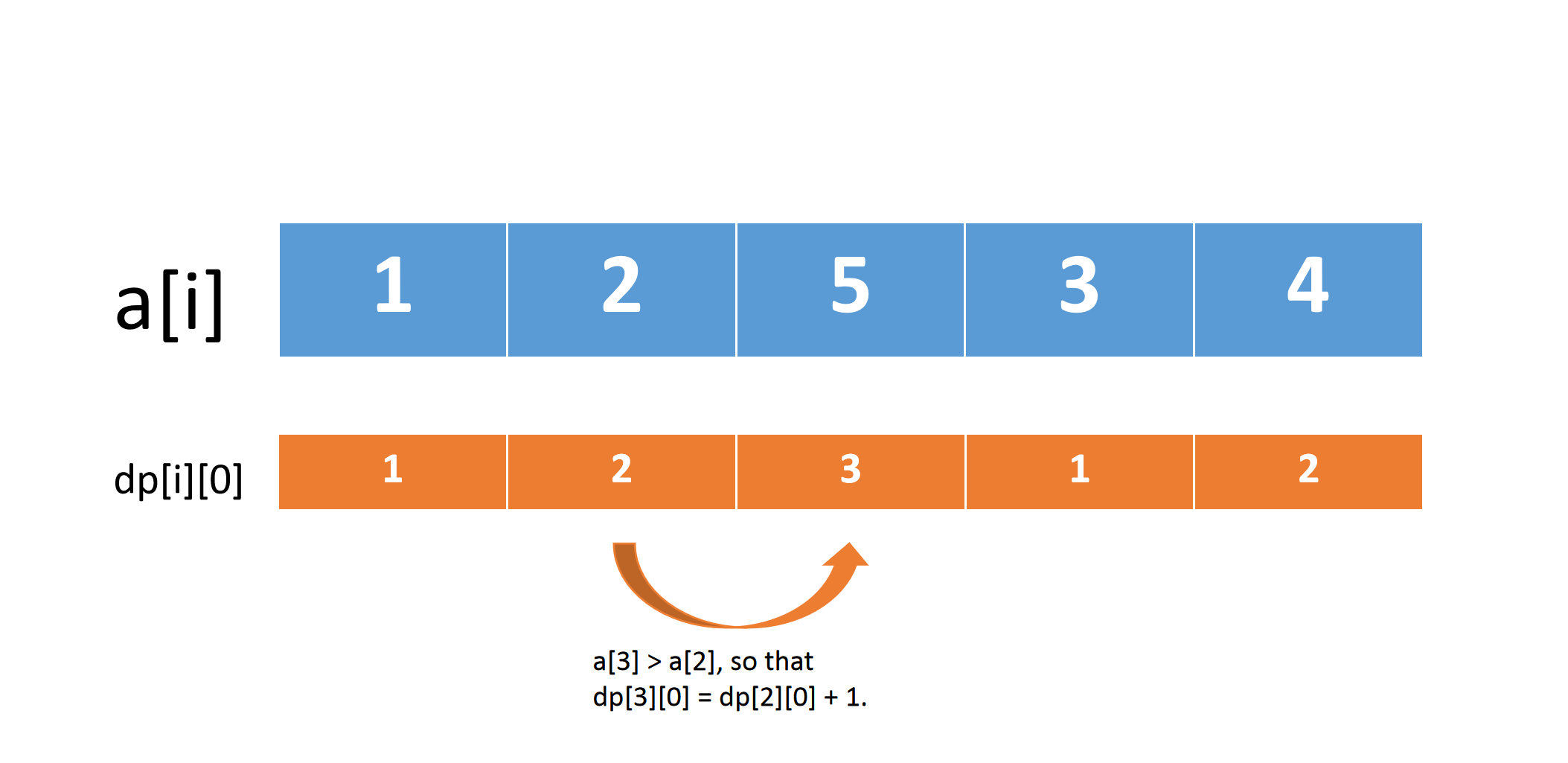
            dp[i][0] = dp[i - 1][0] + 1;
            dp[i][1] = dp[i - 1][1] + 1;
        }
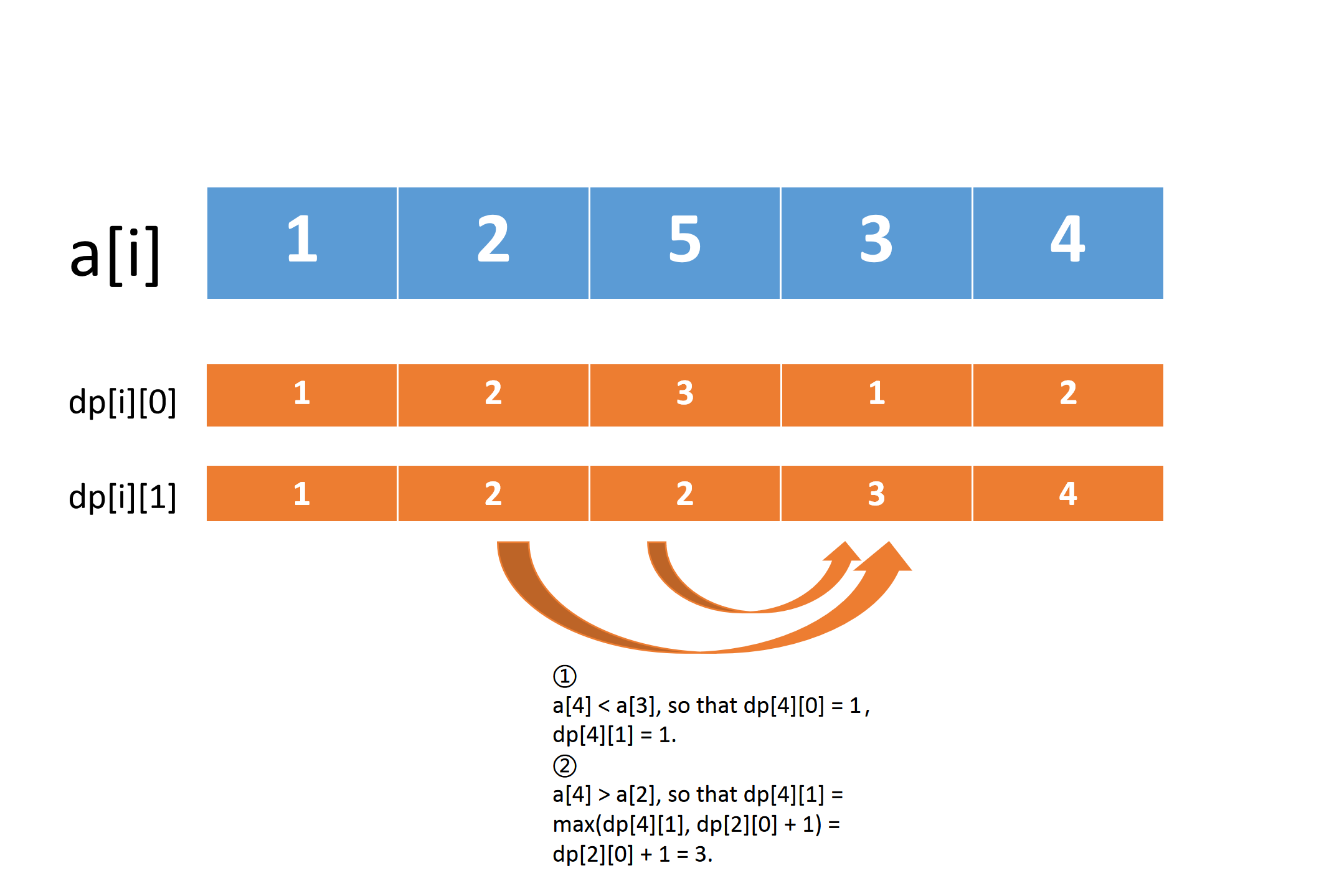
        if(a[i] > a[i - 2])
            dp[i][1] = max(dp[i][1], dp[i - 2][0] + 1);
    }
    
    int maxx = 0;
    for(int i = 1; i <= n; i ++)     //找到最大值.
        maxx = max(maxx, dp[i][1]);       
    printf("%d", maxx);

    return 0;
}

[CodeForces - 1272D] Remove One Element 【线性dp】

原文：https://www.cnblogs.com/satchelpp/p/12059245.html