【网络流相关】二分图匹配

Luogu P3386
首先看看二分图的定义：

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。——百度百科

举个例子：这样的一个图就是二分图。

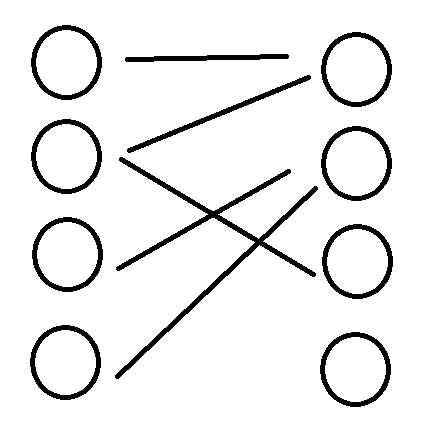
那么什么叫做二分图的匹配？
也就是在二分图中选择若干条边，其中任意两条边的端点不相同。此时边集元素的个数就是二分图的一个匹配。
那么很显然二分图的最大匹配就是边集个数最多的情况。
举个例子：
下面图中红色边构成了一个二分图匹配

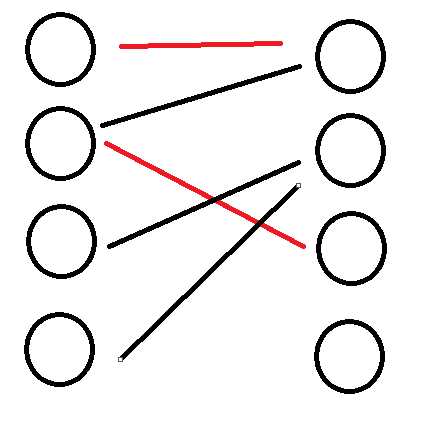
下面图中红色边不构成二分图匹配

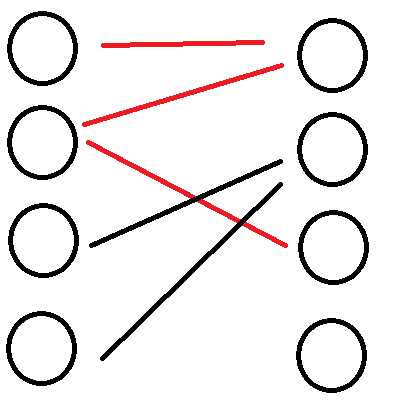
对于二分图最大匹配的问题，我们通常匈牙利算法或者网络最大流来解决。
我完全没有学过匈牙利算法，所以 本文着重于网络最大流。
不过其实没什么好分析的
如图所示：对二分图建立一个超级源点和一个超级汇点，源点向点集\(A\)连一条容量为\(1\)的边，点集\(B\)x向汇点连一条容量为\(1\)的边，然后跑一遍最大流即可。

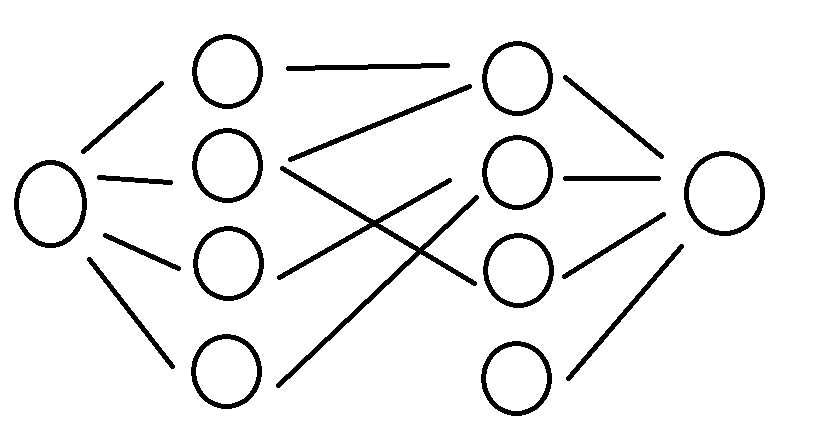
由于在二分图中\(Dinic\)算法的效率非常高，甚至高于匈牙利算法，所以我们通常使用\(Dinic\)跑二分图匹配

#include<cstdio>
#include<queue>
using namespace std;
int n,m,num,cnt,u,v,head[2005],cur[2005],dis[2005],ans;
bool vis[2005];
struct data
{
    int to,next,val;
}e[5000005];
void add(int u,int v,int val)
{
    e[++cnt].to=v;
    e[cnt].next=head[u];
    head[u]=cnt;
    e[cnt].val=val;
}
bool bfs(int s,int t)
{
    queue<int> que;
    que.push(s);
    for (int i=1;i<=n+m+2;i++) dis[i]=0,vis[i]=false,cur[i]=head[i];
    vis[s]=true;
    dis[s]=1;
    while (!que.empty())
    {
        int now=que.front();
        que.pop();
        for (int i=head[now];i;i=e[i].next)
        {
            v=e[i].to;
            if (!vis[v]&&e[i].val>0)
            {
                dis[v]=dis[now]+1;
                vis[v]=true;
                if (v==t) return true;
                que.push(v);
            }
        }
    }
    return false;
}
int dfs(int now,int t,int flow)
{
    if (!flow||now==t) return flow;
    int used=0;
    for (int i=cur[now];i;i=e[i].next)
    {
        cur[now]=i;
        v=e[i].to;
        if (dis[now]+1!=dis[v]) continue;
        int tmp=dfs(v,t,min(flow-used,e[i].val));
        if (tmp)
        {
            e[i].val-=tmp;
            e[i^1].val+=tmp;
            used+=tmp;
            if (flow-used==0) return flow;
        }
    }
    return used;
}
void Dinic(int s,int t)
{
    while (bfs(s,t)) ans+=dfs(s,t,0x7fffffff);
}
int main()
{
    scanf("%d%d%d",&n,&m,&num);
    cnt=1;
    for (int i=1;i<=num;i++)
    {
        scanf("%d%d",&u,&v);
        if (u>n||v>m) continue;
        add(u,v+n,1);
        add(v+n,u,0);
    }
    for (int i=1;i<=n;i++) add(n+m+1,i,1),add(i,n+m+1,0);
    for (int i=n+1;i<=m+n;i++) add(i,n+m+2,1),add(n+m+2,i,0);
    Dinic(n+m+1,n+m+2);
    printf("%d",ans);
    return 0;
}

【网络流相关】二分图匹配

原文：https://www.cnblogs.com/notscience/p/12063388.html