搜索顾名思义,就是一个个地寻找,直到寻找到最优解或者答案为止
搜索经常和递归和栈相关,因为我们需要遍历每个地方的,不管这个分支是否有解都要回溯一下
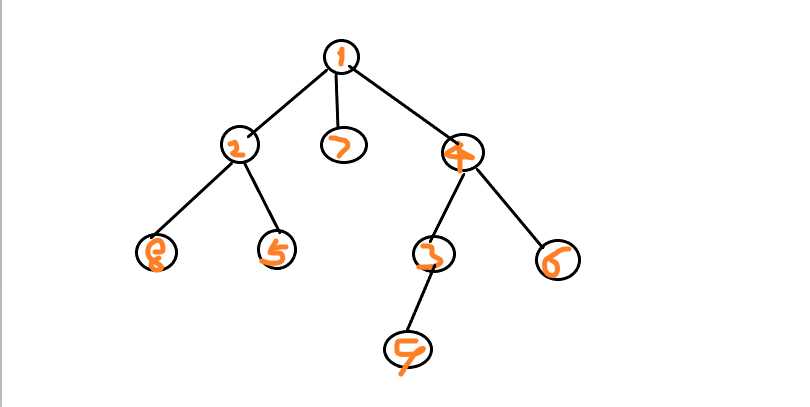
首先我们先熟悉树和图的遍历:
1.存储方式,选择邻接表;这样是很省空间的
邻接表,以表头数组head,使用ver和edge数组分别表示这一条边的终点和权值,使用next数组模拟链表指针

以一个有向图为例:
x,y,z分别表示起点和终点,该边的权值
const int N = 1e3 + 10;
int head[N],edge[N],ver[N],next[N];
int tot = 0;
void add(int x,int y,int z){//添加一条边
ver[++tot] = y; edge[tot] = z;
next[tot] = head[x],head[x] = tot;
}
给出遍历一个有向图的demo
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int head[N],edge[N],ver[N],nex[N];
bool vis[N];
int tot = 0;
void add(int x,int y,int z){//添加一条边
ver[++tot] = y; edge[tot] = z;
nex[tot] = head[x],head[x] = tot;
}
void dfs(int x){
cout << x << " ";
vis[x] = 1;
for(int i = head[x];i;i = nex[i]){
int y = ver[i];
if(!vis[y]) dfs(y);
}
}
int main(){
int n,m;
int x,y,z;
cin >> n >> m;
for(int i = 1;i <= m;i++){
cin >> x >> y >> z;
add(x,y,z);
}
dfs(1);
return 0;
}
关于树的还有一些信息需要我们去找出来,然后也使用深度优先去找的
时间戳:每个结点第一次被访问到时是第几个被访问的
给出代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int head[N],nex[N],ver[N],dfsn[N],d[N];
bool vis[N];
int tot = 0,cur = 0;
void add(int x,int y){
d[y]++;
ver[++tot] = y;
nex[tot] = head[x],head[x] = tot;
}
void dfs(int x){
vis[x] = 1;
dfsn[++cur] = x;
for(int i = head[x]; i ; i = nex[i]){
int y = ver[i];
if(!vis[y]) dfs(y);
}
}
int main ()
{
int n,m,x,y;
cin >> n >> m;
for(int i = 1;i <= m;i++)
{
cin >> x >> y;
add(x,y);
}
for(int i = 1;i <= n;i++)
if(d[i] == 0){
dfs(i);
break;
}
for(int i = 1;i <= n; i ++)
cout << dfsn[i] << " ";
puts("");
return 0;
}
dfs序:就是刚进入递归和回溯是记录该点的编号,最后产生2*N的序列(假设有N个点),同时两个相同数字的序列区间就是一颗子树
给出代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int head[N],nex[N],ver[N],dfsn[N],d[N];
bool vis[N];
int tot = 0,cur = 0;
void add(int x,int y){
d[y]++;
ver[++tot] = y;
nex[tot] = head[x],head[x] = tot;
}
void dfs(int x){
vis[x] = 1;
dfsn[++cur] = x;
for(int i = head[x]; i ; i = nex[i]){
int y = ver[i];
if(!vis[y]) dfs(y);
}
dfsn[++cur] = x;
}
int main ()
{
int n,m,x,y;
cin >> n >> m;
for(int i = 1;i <= m;i++)
{
cin >> x >> y;
add(x,y);
}
for(int i = 1;i <= n;i++)
if(d[i] == 0){
dfs(i);
break;
}
for(int i = 1;i <= n*2
; i ++)
cout << dfsn[i] << " ";
puts("");
return 0;
}
数的深度,我们假设根节点的深度是0,我们直到假设y是x的子节点则 d[y] = d[x] + 1 dfs就可以知道了深度一样代表这些结点在一层
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int head[N],nex[N],ver[N],dfsn[N],d[N],depth[N];
bool vis[N];
int tot = 0,cur = 0;
void add(int x,int y){
d[y]++;
ver[++tot] = y;
nex[tot] = head[x],head[x] = tot;
}
void dfs(int x){
vis[x] = 1;
for(int i = head[x]; i ; i = nex[i]){
int y = ver[i];
if(!vis[y]) {
depth[y] = depth[x] + 1;
dfs(y);
}
}
}
int main ()
{
int n,m,x,y;
cin >> n >> m;
for(int i = 1;i <= m;i++)
{
cin >> x >> y;
add(x,y);
}
for(int i = 1;i <= n;i++)
if(d[i] == 0){
dfs(i);
break;
}
for(int i = 1;i <= n; i ++)
cout << i << " " << depth[i] << endl;
return 0;
}
我们记size[i]为以i为根节点的这个树包含的结点数量,包括本节点
树的重心:去掉该节点,然后剩下的子树中最大的size[i]相比去掉其他结点j后剩下的子树中最大的size[j]是最小的
对于结点i它的size等于所有儿子的size加上自己1
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int head[N],ver[N],nex[N],size[N],ig[N];
bool vis[N];
int ans,pos,tot = 0;
int n,m;
void add(int x,int y){
ver[++tot] = y;
ig[y]++;
nex[tot] = head[x]; head[x] = tot;
}
void dfs(int x){
vis[x] = 1;
size[x] = 1;
int max_part = 0;
for(int i = head[x]; i ; i = nex[i]){
int y = ver[i];
if(!vis[y]){
dfs(y);
size[x] += size[y];
max_part = max(max_part,size[y]);
}
}
max_part = max(max_part,n - size[x]);
if(max_part < ans){
ans = max_part;
pos = x;
}
}
int main(){
int x,y;
cin >> n >> m;
ans = n + 1;
for(int i = 1;i <= m;i++){
cin >> x >> y;
add(x,y);
}
for(int i = 1;i <= n;i++)
if(!ig[i]){
dfs(i);
break;
}
puts("");
for(int i = 1;i <= n;i++)
cout << i << " " << size[i] << endl;
cout << pos << " " << ans << endl;
return 0;
}
dfs还可以统计无向图有多少联通块,在main()函数中
int cnt = 0;
for(int i = 1;i <= n;i++)
if(!vis[i]) {
dfs(i);
cnt++;
}
下面说一下广度优先搜索bfs
广度就是一层层遍历,先遍历入度为0的节点,需要用到队列
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int head[N],ver[N],nex[N],d[N];
int tot = 0;
void add(int x,int y){
ver[++tot] = y;
nex[tot] = head[x];
head[x] = tot;
}
void bfs(){
queue<int> q;
q.push(1); d[1] = 1;
while(q.size()){
int cur = q.front(); q.pop();
cout << cur << " ";
for(int i = head[cur]; i ; i = nex[i]){
int y = ver[i];
if(d[y]) continue;
d[y] = d[cur] + 1;
q.push(y);
}
}
puts("");
}
int main(){
int n,m,x,y;
cin >> n >> m;
for(int i = 1;i <= m;i++){
cin >> x >> y;
add(x,y);
}
bfs();
return 0;
}
拓扑排序:就是这些结点的遍历是有顺序的,必须有先后关系
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int ver[N],head[N],nex[N],ig[N];
int tot = 0,n,m;
void add(int x,int y){
ver[++tot] = y;
ig[y]++;
nex[tot] = head[x];
head[x] = tot;
}
void topsort(){
queue<int> q;
for(int i = 1;i <= n;i++){
if(!ig[i]) q.push(i);
}
while(q.size()){
int cur = q.front(); q.pop();
cout << cur << " ";
for(int i = head[cur]; i ; i = nex[i]){
int y = ver[i];
if(--ig[y] == 0) q.push(y);
}
}
puts("");
}
int main(){
int x,y;
cin >> n >> m;
for(int i = 1;i <= m;i++){
cin >> x >> y;
add(x,y);
}
topsort();
return 0;
}
接下来做几个题来看看吧
原文:https://www.cnblogs.com/mch5201314/p/12063369.html