CANDECOMP(canonical decomposition)和PARAFAC(parallel factors)是一种对张量进行拆分的方法, 其核心思想是用有限个的秩1张量的和来(近似地)表示该张量. 这种方法被很多人独立的发现, 不考虑历史上的因素, 我们将其称为CP分解法 (CP decomposition).
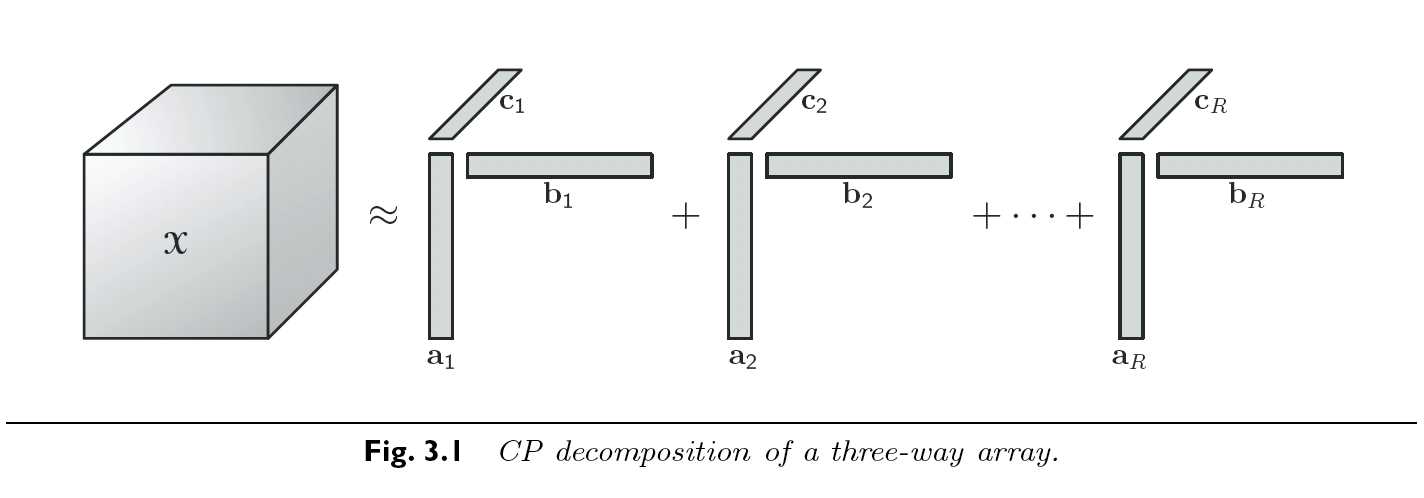
例: 如果我们要把一个3阶张量\(\mathcal{X}\in\mathbb{R}^{I \times J \times K}\)进行CP分解, 我们期待其结果如下.
\[
\begin{equation}
\mathcal{X} \approx \sum_{r=1}^R a_r \circ b_r \circ c_r
\end{equation},
\]
通过外积的定义, 对每个元素都有:
\[
x_{ijk} \approx \sum_{r=1}^R a_{ir}b_{jr}c_{kr} \text{ for $i=1,\dots,I,\,j=1,\dots,J, \, k=1,\dots,K.$}
\]
我们称那些上式中通过外积组成秩1张量元素的向量集合为因子矩阵(factor matrices). 例如, \(\mathrm{A} = \begin{bmatrix} a_1 & a_2 & \dots & a_R \end{bmatrix}\), 类似的,我们构造\(\mathrm{B}\) 和 \(\mathrm{C}\). 利用这些定义, CP分解可以被等价写作以下矩阵形式. 注意, 其左侧都是张量的对应mode的矩阵化.
\[
\mathrm{X}_{(1)} \approx \mathrm{A}(\mathrm{C}\odot \mathrm{B})^\mathsf{T},\\mathrm{X}_{(2)} \approx \mathrm{B}(\mathrm{C}\odot \mathrm{A})^\mathsf{T},\\mathrm{X}_{(3)} \approx \mathrm{C}(\mathrm{B}\odot \mathrm{A})^\mathsf{T}.
\]
以上3维模型也可以用张量的frontal slices来表示:
\[
\mathcal{X} \approx \mathrm{A}\mathrm{D}^{(k)}\mathrm{B}^\mathsf{T},\, \text{ where }\, \mathrm{D}^{(k)} \equiv \text{diag}(c_{k::}) \, \text{ for $\, k=1,...,K.$}
\]
我们也可以将上式子改写为horizontal slices和lateral slices的版本, 需要注意的是, 这种以slice为主体的表达很难延伸到超过3维的张量之中. 利用Kolda的命名方式, 我们也可以进一步简化CP模型:
\[
\mathcal{X} \approx [\![\mathrm{A,B,C]}\!] \equiv \sum_{r=1}^R \mathrm{a}_r \circ \mathrm{b}_r \circ \mathrm{c}_r.
\]
为了便利, 我们通常假设\(\mathrm{A, B}\)和\(\mathrm{C}\)的列向量都是归一化的(normalized). 而原本的比重(weights)则被一个向量\(\lambda\in\mathbb{R}^R\)所吸收, 写作以下形式:
\[
\mathcal{X} \approx [\![\lambda \, ; \, \mathrm{A,B,C}]\!] \equiv \sum_{r=1}^R \lambda_r \: \mathrm{a}_r \circ \mathrm{b}_r \circ \mathrm{c}_r.
\]
其中 \(\Lambda = diag(\lambda).\)
与矩阵时的定义类似, 张量秩写作$ \text{rank}(\mathcal{X}) \(, 为还原张量所需秩1张量的最小数目. 换句话说, 也就是精确(exact)CP分解中的最小成分数. 当CP分解是精确的, 也就是\)R=\text{rank}(\mathcal{X})$时, 我们也称之为秩分解(rank decomposition).
这个张量在 \(\mathbb{R}\) 下的秩为3, 但在 \(\mathbb{C}\) 下的秩为2. 其 \(\mathbb{R}\) 之下的秩分解\(\mathcal{X} = [\![\mathrm{A}, \mathrm{B}, \mathrm{C}]\!]\)为:
\[ \mathrm{A} = \begin{bmatrix}1 & 0 & 1 \\ 0 & 1 & -1 \end{bmatrix}, \quad \mathrm{B} = \begin{bmatrix}1 & 0 & 1 \\ 0 & 1 & 1 \end{bmatrix}, \quad and \quad \mathrm{C} = \begin{bmatrix}1 & 1 & 0 \\ -1 & 1 & 1 \end{bmatrix}, \]
或许读者已经注意到了, 我们给出了张量秩的定义, 但我们没有给出如何求他的方法. 这是张量秩和矩阵秩的第二个巨大不同. 张量秩没有一个简单直接的求法, 以至于任何张量秩都伴随着证明他确实为秩的过程. 即使我们对秩的最大值有一定程度的了解, 直接求秩本身已被证明是NP-hard.
除了最大秩以外, 我们定义典型秩为那些出现概率不为0的秩. 当给定尺寸的张量中填上随机实数值,我们用monte-carlo法等检测其秩为某数的概率. 当其概率不为0时, 我们称之为典型秩. 比如, 我们发现\(2 \times 2 \times 2\)张量中, 79%的可能性是秩2, 21%可能性是秩3. 秩1理论可能,但概率为0. (试想随机生成的一个张量恰好为3个秩1向量外积的可能性).
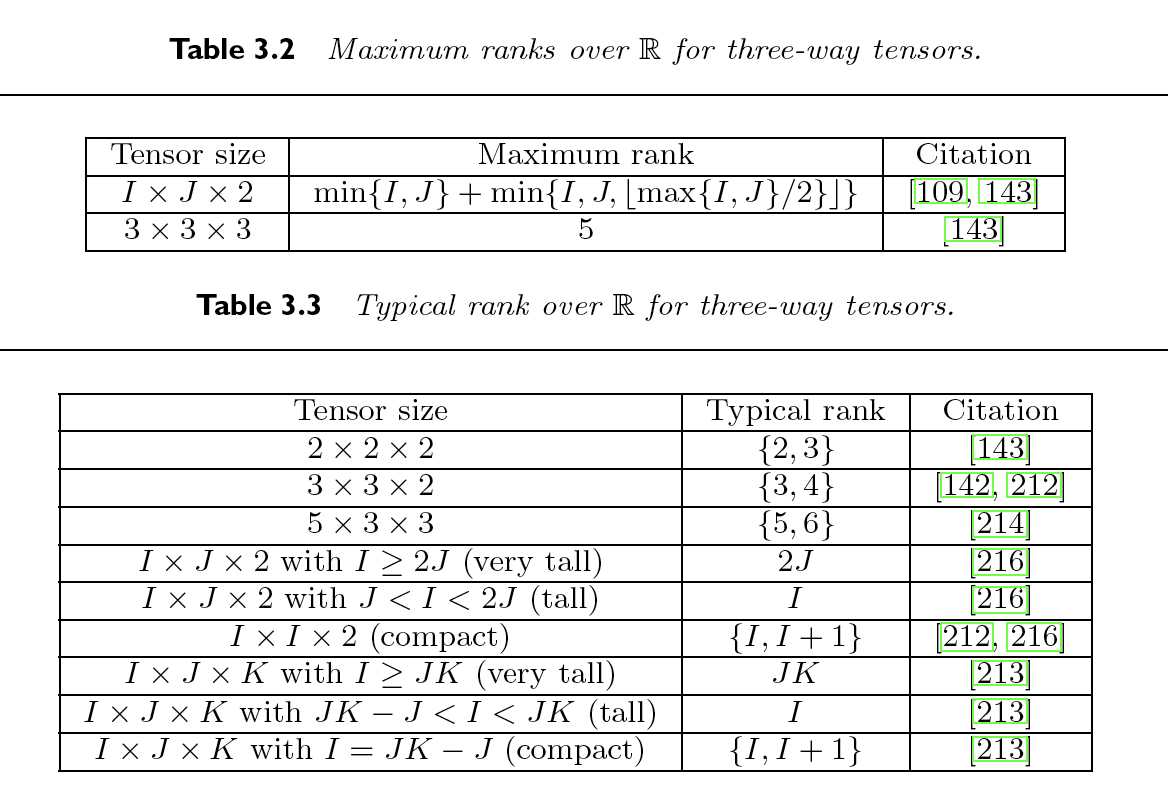
下图是一些在某些情况下我们知道的最大秩(maximum rank)和典型秩(typical rank), 其中最详细的是某维度下只有两层slice的3阶张量:
\[ \text{rank}(\mathcal{X}) \leq \text{min}\{IJ, IK, JK\}. \]

\[ \text{rank}_S(\mathcal{X}) = \Bigg\lceil \frac{{I+N-1}\choose{N}}{I} \Bigg\rceil, \]
高维张量的另一个很神奇的特性在于他们的秩分解往往是唯一的. 而矩阵并不是, 他们往往有多个秩分解解法. 我们可以从一个简单的例子来复习如何轻易构造出无穷多个这样的矩阵秩分解.
令矩阵\(\mathrm{X} \in \mathbb{R}^{I \times J}\), 则他的秩分解为:
\[
\mathrm{X} = \mathrm{A}\mathrm{B}^\mathsf{T} = \sum_{r=1}^R \mathrm{a}_r \circ \mathrm{b}_r.
\]
如果\(\mathrm{X}\)的SVD为\(\mathrm{U\Sigma V}^\mathsf{T}\)那么, 我们可以选择\(\mathrm{A} = \mathrm{U \Sigma}\)和\(\mathrm{B} = \mathrm{V}.\) 然而, 这也等效于选择\(\mathrm{A} = \mathrm{U \Sigma W}\)和\(\mathrm{B} = \mathrm{VW}\), 其中 \(\mathrm{W}\) 是任意一个 \(R\times R\)的正交矩阵(orthogonal matrix)
换句话说, 我们可以找到无穷多个满足上述要求的矩阵秩分解. SVD的结果是唯一理由仅仅是因为其正交限制及对奇异值排序上的约束所导致.
然而, CP分解在弱的多的前提下也是唯一的.令\(\mathcal{X} \in \mathbb{R}^{I \times J \times K}\)为一个秩\(R\)三阶张量, 那么我们有如下分解:
\[
\mathcal{X} = \sum_{r=1}^R \mathrm{a}_r \circ \mathrm{b}_r \circ \mathrm{c}_r = [\![\mathrm{A},\mathrm{B},\mathrm{C}]\!]. \quad\quad\quad\quad\quad(3.1)
\]
上述的唯一性指的是, 我们只能找到一种可能的秩1张量的组合使得他们的和为\(\mathcal{X}\). 请注意, 由于张亮的特殊性, 我们在讲唯一时排除了张量的度量(scaling)和置换(permutation)上的内在不确定性(indeterminacy).
置换不确定性是因为任何秩1张量都可以被随意交换维度. 写成数学语言便是:
\[
\mathcal{X} = [\![\mathrm{A}, \mathrm{B}, \mathrm{C}]\!]
= [\![\mathrm{A\Pi}, \mathrm{B\Pi}, \mathrm{C\Pi}]\!] \,\text{ for any $R \times R$ permutaton matrix $\mathrm{\Pi}$}.
\]
而度量的不确定性则来自于我们可以缩放组成秩1张量的向量, 只要保证他们最后的外积不便即可:
\[ \mathcal{X} = \sum_{r=1}^{R}(\alpha_r \mathrm{a}_r) \circ (\beta_r \mathrm{b}_r) \circ (\gamma_r \mathrm{c}_r), \quad \alpha_r \beta_r \gamma_r = 1 \text{ for }r=1,\dots,R. \]
在唯一性这方面最有建树的理论之一来自于Kruskal和新概念k-rank. 对于一个矩阵\(\mathrm{A}\)来说, k-rank, 写作\(k_\mathrm{A}\),是满足A的任意k个列向量都是线性不相关的条件下的k的最大值. 该k揭示了CP分解法(3.1)唯一性的充分条件:
\[
k_{\mathrm{A}} + k_{\mathrm{B}} + k_{\mathrm{C}} \geq 2R + 2.
\]
随后, Kruskal的结论被其他人延伸至N阶张量. 设\(\mathcal{X}\)是一个N阶的秩R张量, 并假设其CP分解如下:
\[ \mathcal{X} = \sum_{r=1}^R \mathrm{a}_r^{(1)}\circ \mathrm{a}_r^{(2)} \circ \dots \circ \mathrm{a}_r^{(N)} = [\![\mathrm{A}^{(1)}, \mathrm{A}^{(2)},\dots,\mathrm{A}^{(N)}]\!]. \]
\[ \sum_{n=1}^N k_\mathrm{A}^{(n)} \geq 2R + (N-1). \]
然而我们通过观察发现, \(\text{rank}(\mathrm{A} \odot \mathrm{B}) \leq \text{rank} (\mathrm{A} \otimes \mathrm{B}) \leq \text{rank}(\mathrm{A}) \cdot \text{rank}(\mathrm{B})\), 我们可以甚至可以得出一个更简单的必要条件:
\[
\min_{n=1,\dots,N}\Bigg(\prod_{m=1 \\ m \neq n} \text{rank}(\mathrm{A}^{(m)})\Bigg) \geq R.
\]
De Lathauwer 提出了观察张量秩是否为确定唯一(deterministically unique)或generically unique (一般唯一, 也就是概率为1). CP分解法对一个\(\mathcal{X} \in \mathbb{R}^{I \times J \times K}\)的一般唯一条件如下:
\[
R \leq K \quad \text{and} \quad R(R-1) \leq I(I-1)J(J-1)/2.
\]
类似的, 对于一个4阶秩R张量$\mathcal{X} \in \mathbb{R}^{I \times J \times K \times L}来说, CP分解法的一般唯一条件为:
\[
R \leq L \quad \text{and} \quad R(R-1) \leq IJK(3IJK - IJ - IK - JK - I - J - K +3)/4
\]
对矩阵来说, 我们知道使用SVD的前k个因子即可获得其最好的秩k近似(rank-k approximation). 我们来复习一下. 若秩R矩阵\(\mathrm{A}\)的SVD如下:
\[
\mathrm{A} = \sum_{r=1}^R \sigma_r \mathrm{u}_r \circ \mathrm{v}_r \quad \text{with }\sigma_1 \geq \sigma_2 \geq \dots \geq \sigma_R > 0.
\]
最小化\(||\mathrm{A} - \mathrm{B}||\)的秩k近似为:
\[ \mathrm{B}= \sum_{r=1}^k \sigma_r \mathrm{u}_r \circ \mathrm{v}_r. \]
理想状态下, 我们期待将其中k个分解因子相加来获得一个最佳k秩近似. 但实际上, 这并不可行. Kolda已经给出一个反例, 其中最佳秩1近似的因子, 并不存在于其最佳秩2分解的因子中. 换句话说, 我们不能通过寻找秩N分解因子集, 来按序给出秩N以下的最佳近似. 我们必须独立的面对每个秩k问题, 并同时找出其所有因子.
其中, \(\mathrm{A} \in \mathbb{R}^{I \times 2}, \, \mathrm{B} \in \mathbb{J \times 2}, \quad \mathrm{C} \in \mathbb{R}^{K \times 2}\) 并且其列向量均为线性无关. 那么, 这个张量就可以被一个秩2张量近似至任意程度:
\[ \mathcal{Y} = \alpha \, \Big( \mathrm{a}_1 + \frac{1}{\alpha} \mathrm{a}_2 \Big) \circ \Big( \mathrm{b}_1 + \frac{1}{\alpha} \mathrm{b}_2 \Big) \circ \Big( \mathrm{c}_1 + \frac{1}{\alpha} \mathrm{c}_2 \Big) - \alpha \, \mathrm{a}_1 \circ \mathrm{b}_1 \circ \mathrm{c}_1. \]
具体来说:
\[
||\mathcal{X} - \mathcal{Y}|| = \frac{1}{\alpha} \Bigg|\Bigg| \,
\mathrm{a}_2 \circ \mathrm{b}_2 \circ \mathrm{c}_1 + \mathrm{a}_2 \circ \mathrm{b}_1 \circ \mathrm{c}_2 + \mathrm{a}_1 \circ \mathrm{b}_2 \circ \mathrm{c}_2 + \frac{1}{\alpha} \mathrm{a}_2 \circ \mathrm{b}_2 \circ \mathrm{c}_2 \,\Bigg|\Bigg|
\]
很显然, 此式可以被缩小至任意程度. 因此上述张量为退化的. 从这个例子中我们还可以发现, 秩2张量空间并不是闭合(closed)的. 此例中, 如下图所示的那样, 秩2向量的序列收敛于秩3张量.

接下来快速的叙述一些关于此性质的重要发现. Lundy, Harshman 和 Kruskal发现结合Tucker分解法可以避免退化. De Silva和Lima指出, 那些没有最优秩k近似的张量, 至少对某些k来说有正体积(Lebesgue measure 勒贝格测度). 换句话说, 没有最优秩k近似并不是一个罕见的事件. Comon给出了对称矩阵和对称近似的相似退化例子. Stegeman证明了维度为\(I\times \times 2\)时, 任何秩为\(I+1\)的张量都不存在最佳秩\(I\)近似. 他接下来又证明了当张量的维度为\(I\times J\times 3\), 秩为其2种典型秩时, 绝大多数情况下我们可以找到一个近似至任意程度的低秩近似.
当最佳低秩近似不存在时, 考虑其边界秩(border rank)变得十分有用. 他被定义为允许我们近似至任意精度时, 所需秩1张量的数量的最小值:
\[
\widetilde{\text{rank}} (\mathcal{X}) = \min \{ \, r \, | \, \text{ for any $\epsilon > 0$, there exists a tensor $\mathcal{E}$ such that $||\mathcal{E}|| < \epsilon$ and rank $(\mathcal{X} + \mathcal{\mathcal{E}} = r)$}\}
\]
显然, 边界秩满足:
\[ \widetilde{\text{rank}}(\mathcal{X}) \leq \text{rank}(\mathcal{X}). \]
就如前文所述, 并没有一个确定的算法来得出一个张量的秩. 于是, 当我们试图计算CP分解时遇到的第一个问题, 便是如何选择其秩1成分的个数. 许多计算方法同时选择了几个不同的秩1成分个数来计算CP分解, 直到发现某一种选择看起来"最好". 理想上来说, 如果数据是没有噪音而且秩1成分数量给定后的CP计算方法是已知的, 那么我们只要在分解的拟合精度达到100%之前, 对\(R= 1,2,3,\dots\)依序进行计算即可.

假设三阶张量\(\mathcal{X} \in \mathbb{R}^{I \times J \times K}\). 我们的目标是算出他的CP分解, 使得其中R个秩1元素的和能够最好的近似\(\mathcal{X}\). 也就是说, 我们要寻找
\[
\min_{\hat{\mathcal{X}}} ||\mathcal{X} - \hat{\mathcal{X}}|| \, \text{ with }
\, \hat{\mathcal{X}} = \sum_{t=1}^R \lambda_r \, \mathrm{a}_r \circ \mathrm{b} \circ \mathrm{c}_r = [\![\mathrm{\lambda}\, ; \, \mathrm{A}, \mathrm{B}, \mathrm{C}]\!].
\]
交替最小方差法先固定\(\mathrm{B}\)和\(\mathrm{C}\)来求出\(\mathrm{A}\), 然后固定\(\mathrm{A}\)和\(\mathrm{C}\)来求\(\mathrm{B}\), 最后固定\(\mathrm{A}\)和\(\mathrm{B}\)来求出\(\mathrm{C}\). 然后将重复整个流程直到一些收敛条件被符合.
因此, 最小化问题可以被写成以下矩阵形式
\[ \min_{\hat{\mathrm{A}}}||\mathrm{X}_{(1)} - \hat{\mathrm{A}}(\mathrm{C}\odot\mathrm{B})^\mathsf{T}||_F, \]
\[ \hat{\mathrm{A}} = \mathrm{X}_{(1)}\big[(\mathrm{C}\odot \mathrm{B})^{\mathsf{T}}\big]^\dagger. \]
由于Khatri-Rao乘积的性质, 其伪逆矩阵有特殊形式. (可参考本笔记开头介绍Khatri-Rao性质的部分). 经常将解写作
\[
\hat{\mathrm{A}} = \mathrm{X}_{(1)}(\mathrm{C} \odot \mathrm{B})(\mathrm{C}^{\mathsf{T}}\mathrm{C} * \mathrm{B}^{\mathsf{T}}\mathrm{B})^\dagger.
\]
这个版本的优势在于我们仅仅需要计算一个\(R\times R\)而不是\(JK\times R\)矩阵的伪逆矩阵. 然而, 由于存在数值病态条件的可能, 我们并不总是推荐这个版本.
最后, 我们还需要归一化\(\hat{\mathrm{A}}\)的列向量来获得\(\mathrm{A}\). 换句话说, 令\(\lambda_r = ||\hat{\mathrm{a}}_r||\) 及 \(\mathrm{a}_r = \hat{\mathrm{a}}_r / \lambda_r \, \text{ for } r = 1,\dots , R.\)
如图中所述, 在每个内迭代中, 都必须计算矩阵\(\mathrm{V}\)的伪逆矩阵. 虽然这只是个\(R\times R\)尺寸的矩阵. 迭代将持续到某些停止条件都被符合为止. 常见的选择有: 目标函数的提升为0或低于阈值; 因子矩阵几乎或没有被改变; 目标值为0或几乎为0以及预设的最大迭代次数被超过等. (熟悉深度学习的朋友应该都很熟悉这些常见的停止模式)
ALS算法简单易懂, 实现轻松, 但往往需要很多次迭代才能收敛, 显得效率有些低. 而且, 该算法并不保证我们能达到一个全局最小值, 甚至不能保证是一个驻点. 他其实只是给出了一个上述最小化目标的函数的解, 使得最小化目标函数开始慢慢停止减少, 他没有保证这个最小化目标函数处于最低值或者不会继续减少.
替代ALS的可行算法有许多, 但在时间不是紧缺的情况下, 研究表明并没有一个比ALS全面优秀的算法存在. 研究ALS的变种算法的论文更是不计其数. 他成为了一个分支研究的起点, 人们期待从他出发, 寻找张量分解的新的可能.
下一章我们将引入另一种分解法: Tucker分解法及张量压缩, 敬请期待!!
原文:https://www.cnblogs.com/lywangjapan/p/12068703.html