设\(A(x)\)表示一个\(n-1\)次多项式,则所有项的系数组成的\(n\)维向量\((a_0,a_1,a_2,\dots,a_{n-1})\)唯一确定了这个多项式。
即
\[A(x)=\sum \limits_{i=0}^{n-1}a_ix^i\]
\[=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1}\]
将\(n\)个互不相同的\(x\)代入多项式,会得到\(n\)个互不相同的取值\(y\)。设他们组成的\(n\)维向量分别为\((x_0,x_1,x_2,\dots,x_{n-1}),(y_0,y_1,y_2,\dots,y_{n-1})\)。则给多项式被这两个\(n\)维向量唯一确定。
其中
\[y_i=A(x_i)=\sum \limits_{j=0}^{n-1}a_j\times x_i^j\]
定义两个多项式\(A(x)=\sum\limits_{i=0}^{n-1}a_ix^i\)与\(B(x)=\sum\limits_{i=0}^{n-1}b_ix^i\)相乘的结果为\(C(x)\)。
则
\(C(x)=A(x)\times B(x)=\sum\limits_{k=0}^{2n-2}(\sum \limits_{k=i+j} a_ib_j)x^k\)
形如\(C(k)=\sum \limits_{i\oplus j=k}a_ib_j\)的式子称为卷积,注意到,多项式乘法的本质就是加法卷积。
两个\(n-1\)次多项式相乘,得到的是一个\(2n-2\)次多项式,时间复杂度为\(O(n^2)\)。
若取两个多项式在\(2n-1\)个点处的点值表示,则
\[{y_3}_i=(\sum\limits_{j=0}^{2n-2}a_jx_i^j)\times(\sum\limits_{j=0}^{2n-2}b_jx_i^j)={y_1}_i\times{y_2}_i\]
设\(a,b\)为实数,\(i^2=-1\),形如\(a+bi\)的数叫做复数,其中\(i\)被称为虚数单位。复数域是已知最大的域。
在复平面中,\(x\)轴代表实数,\(y\)轴代表虚数。每一个复数对应复平面上一个从\((0,0)\)指向\((a,b)\)的向量。
向量的长度\(\sqrt{a^2+b^2}\)叫做模长。表示从\(x\)轴正半轴到该向量的转角的有向角叫做幅角。
记\(z_1=(a,b),z_2=(c,d)\)。
复数相加遵循平行四边形法则。\(z_1+z_2=(a+c,b+d)\)。
复数相乘时,模长相乘,幅角相加。\(z_1+z_2=(ac-bd,ad+bc)\)。
下文中,默认\(n\)为2的正整数次幂。
在复平面上以原点为圆心,\(1\)为半径作圆,所得的圆叫单位圆。以原点为起点,圆的的\(n\)等分点为终点,作\(n\)个向量,设幅角为正且最小的向量对应的复数为\(\omega_n\),则称\(\omega_n\)为\(n\)次单位根。
由复数的乘法定义(模长相乘,幅角相加)可知,其余的\(n-1\)个向量对应的复数分别为\(\omega_n^2,\omega_n^3,\dots,\omega_n^n\),且易知\(\omega_n^0=\omega_n^n=1\)。
那么如何计算他们的值呢?
欧拉公式解决了这个问题:
\[\omega_n^k=\cos \frac{k\pi}{n}+\sin \frac{k\pi}{n}\]
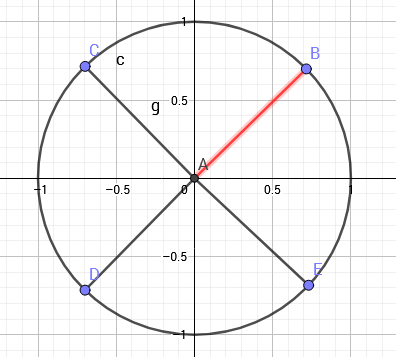
如图,向量\(\overrightarrow{AB}\)表示的复数为\(8\)次单位根,单位根的幅角为\(\frac{\pi}{n}\)
代数中,若\(z^n=1\),则称\(z\)为\(n\)次单位根。
\(\omega_n^k=\cos k\frac{2\pi}{n}+ i\sin k\frac{2\pi}{n}\)
\(\omega_{2n}^{2k}=\omega_n^k\)
从几何意义上来说,在复平面上,二者表示的向量终点相同。
证明:
\[\omega_{2n}^{2k}=\cos 2k \frac{2\pi}{2n}+i\sin 2k\frac{2\pi}{2n}=\cos k\frac{2\pi}{n}+ i\sin k\frac{2\pi}{n}=\omega_n^k\]
证明:
\[\omega_n^{\frac{n}{2}}=\cos \frac{n}{2} \cdot \frac{2\pi}{n}+ i\sin \frac{n}{2} \cdot \frac{2\pi}{n}=\cos \pi+i\sin \pi=-1\]
\[\omega_{n}^{k+\frac{n}{2}}=\omega_n^k\times\omega_n^{\frac{n}{2}}=-\omega_n^k\]
[学习笔记&教程] 信号, 集合, 多项式, 以及各种卷积性变换 (FFT,NTT,FWT,FMT) - rvalue - 博客园
原文:https://www.cnblogs.com/newbielyx/p/12076067.html