不同阶段、不同方式获取的地理信息数据可能采用不同的坐标系。为实现同一区域不同数据成果共享利用,通常需要进行坐标转换。
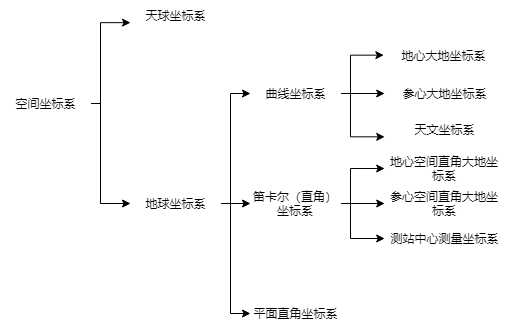
按研究对象的不同,空间坐标系可分为天球坐标系和地球坐标系两大类;按表示方式,地球坐标系又可分为曲线坐标系、空间直角坐标系和平面直角坐标系三种。
 |
1、地心坐标系
椭球定位:总地球椭球在全球范围内与大地水准面有最佳的符合,同时椭球中心与地球质心一致或最接近,即满足全球范围内的大地水准面差距的平方和最小。
椭球定向:1)椭球短轴平行于地球自转轴;2)大地起始子午面平行于天文起始子午面。
(1)CGCS2000大地坐标系
2008年7月1日起,我国全面启用2000国家大地坐标系(CGCS2000,China Geodetic Coordinate System 2000)。CGCS2000实际是ITRF 1997框架在我国的加密和实现,是定义在ITRF 1997框架中的区域性地心坐标框架。通过GPS A、B级网,总参GPS一、二级网,中国地壳运动观测网,地壳运动监测网4个空间网在ITRF 1997框架下联合平差计算站点历元2000.0下的坐标和速度,相对精度达到10-9。
坐标系的原点为地球质心(包括海洋和大气的整个地球的质量中心),Z轴指向BIH1984.0定义的协议地球极CTP方向,X轴指向BIH1984.0定义的零子午面与CTP对应的赤道的交点,Y轴和Z、X轴构成右手坐标系。
4个常用的椭球参数:
| 长半轴 | a = 6378137m |
|
地球扁率 |
f = 1/298.257222101 |
| 地球引力常数 | GM = 3.986004418×1014m3s-2 |
| 地球自转角速度 | ω = 9.292115×10-5rad/s |
(2)WGS84大地坐标系
1984年世界大地坐标系(Word Geodetic System,WGS),由美国建立,是一个协议地球参考系,该坐标系的原点是地球的质心,Z轴指向BIH1984.0(国际时间局)定义的协议地球极CTP方向,X轴指向BIH1984.0零度子午面和CTP对应的赤道的交点,Y轴和Z、X轴构成右手坐标系。坐标系采用1979年国际大地测量与地球物理联合会(IUGG)第17届大会上推荐的椭球参数。WGS84由分布于全球的一系列GPS跟踪站的坐标来具体体现,此坐标框架先后经历了几次更新,其坐标参考历元也不断在改变。
4个常用的椭球参数:
| 长半轴 | a = 6378137m |
|
地球扁率 |
f = 1/298.257223563 |
| 地球引力常数 | GM = 3.986004418×1014m3s-2 |
| 地球自转角速度 | ω = 9.292115×10-5rad/s |
2、参心坐标系
椭球定位:参考椭球面在一定范围内与大地水准面有最佳的符合,对椭球中心位置无特殊要求。
椭球定向:1)椭球短轴平行于地球自转轴;2)大地起始子午面平行于天文起始子午面。
有了定位和定向的参考椭球面就成为一个基准面,根据不同的定位和定向,同一个椭球可对应不同的基准面。
西安80、北京54均为参心坐标系。椭球参数略。
3、平面直角坐标系
利用一定的数学法则将空间三维坐标变换到二维投影面上,构成平面直角坐标系。
(1)高斯平面直角坐标系
我国1:100万比例尺地形图采用等角圆锥投影,1:50万及更大比例尺地形图都采用高斯克吕格投影(横轴等角切椭圆柱投影),为了限制长度变形,规定按经差6°和3°进行投影分带,其中1:2.5万—1:50万比例尺地形图上采用6°分带,大于等于1:1万地形图采用3°分带。在投影面上,以中央子午线的投影为纵轴,以赤道的投影为横轴,为了避免出现负的横坐标值,横坐标统一增加500Km。为了区别作业区域属于哪一投影带,可在横坐标的百千米位数前加上带号。例如某点的坐标值为东坐标34425480.3,北坐标4270568.2,其中34为带号。
(2)独立平面直角坐标系
高斯平面直角坐标系在高海拔地区和距离中央子午线比较远的地方,投影长度的变形会比较大,无法满足城市测量、工程测量中位置精度要求,因此会根据实际情况建立相应的地方独立平面直角坐标系。
地方独立平面直角坐标系与高斯平面直角坐标系相比,主要存在以下差异:
a.中央子午线选在该区域的中央;
b.参考椭球面为该区域的平均高程面;
c.人为指定坐标原点和坐标轴指向。
4、高程系统
正高:以大地水准面为高程基准面,地面上任一点的正高高程(简称正高),即该点沿垂线方向至大地水准面的距离。
正常高:将正高系统中不能精确测定的重力加速度平均值 用正常重力加速度平均值 代替,得到的一种高程系统,称为正常高。
我国规定采用正常高高程系统作为我国高程的统一系统。
现行1985国家高程基准:高程基准面根据青岛验潮站1952年至1979年19年间的验潮资料计算确定。(原点高程为72.260m)。
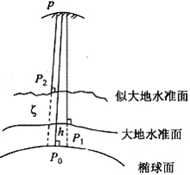
大地高:地面点沿椭球面法线方向至椭球面的距离。
大地高H与正高 H正、正常高H正常 之间的关系:
H = H正 + N
H = H正常+ ξ
N为大地水准面差距, ξ为高程异常。
原文:https://www.cnblogs.com/xiangze/p/12008408.html