迪杰斯特拉算法 Dijkstra

目录

• 引入以及简单介绍
• 迪杰斯特拉算法dijkstra
• 代码

引入以及介绍

在经过我们学习了 广度优先搜索(如果不知道的话...点这里) 之后,我们已经可以找到了从A点到达E点的一条最短路径。只不过寻找这个路径比较麻烦,并且浪费时间。

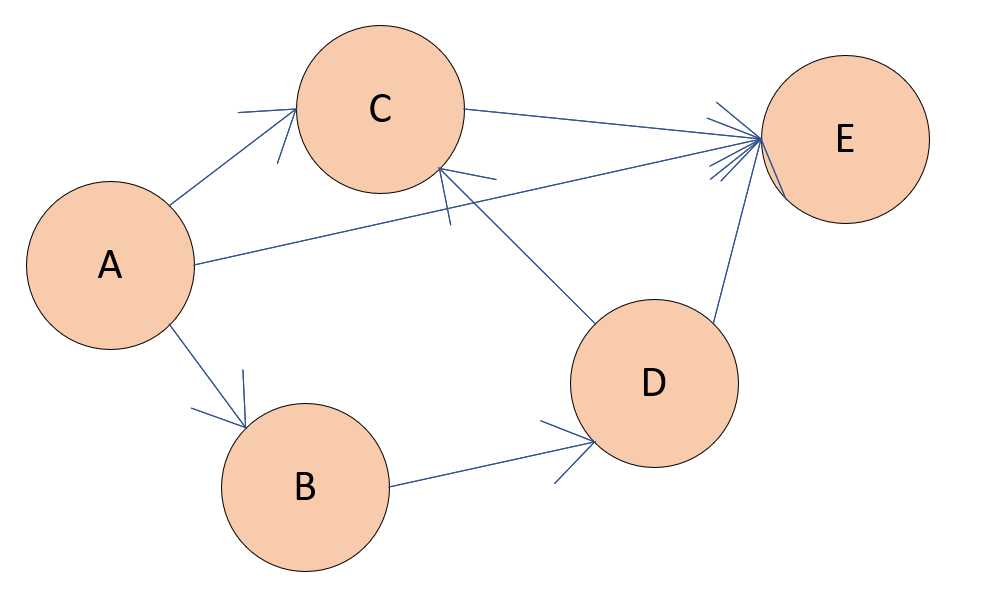
当然,我们经过广度优先搜索的路径,只能说是一个最短路径,因为它经过的路的条数是最少的。就好比如下面的图片......

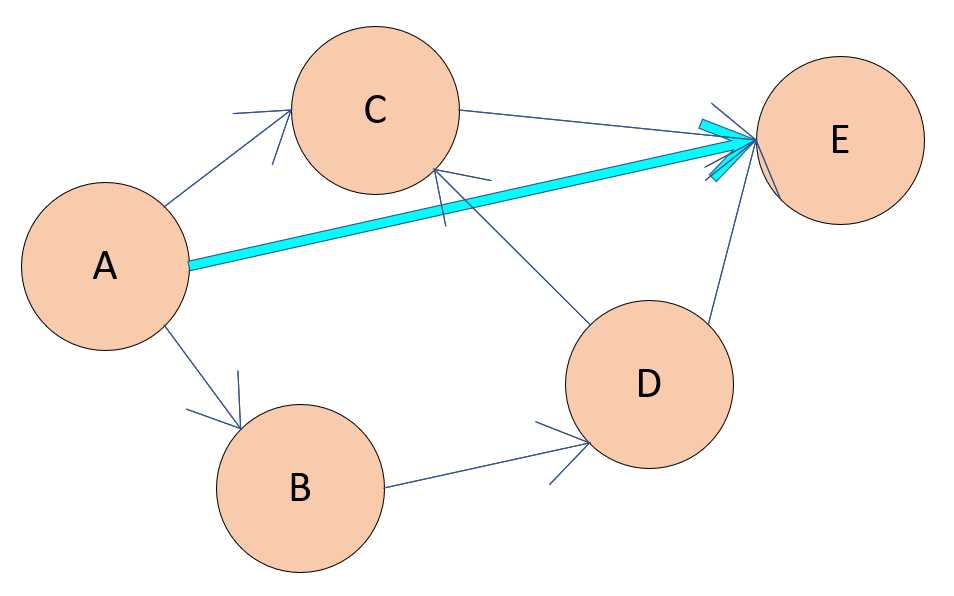
如果我们给这些道路加上了一些东西,比如什么呢,加上了一些从开始地点到达结束地点的时间的话,那么你就可以发现了,我们刚刚利用广度优先搜索所得的路径并不是最省时间的。同时的话,你还可以发现一条更短的路径......

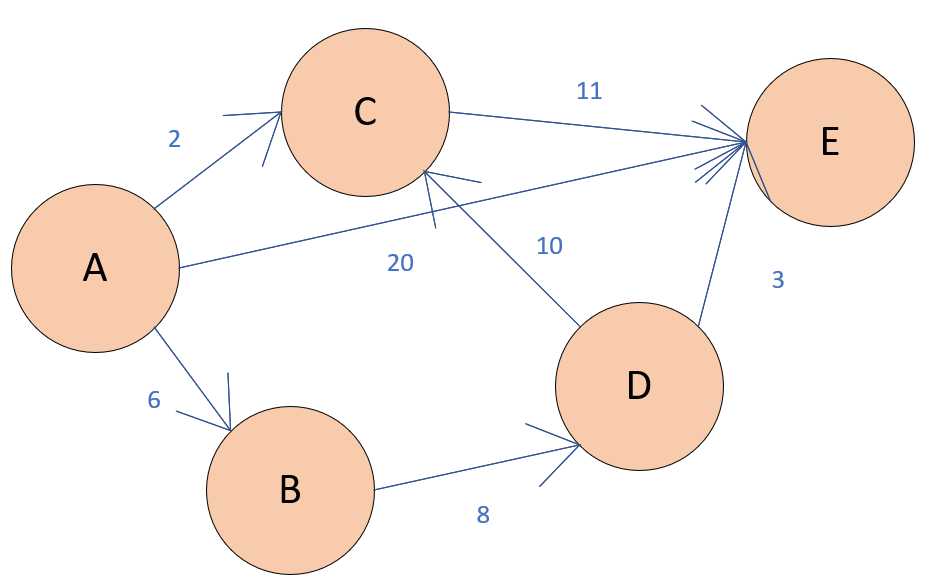
在学习广度优先搜索的时候,我们是找出了路径最短的那个路径,也就是,段数最少的那个路段。而接下来我们要进行学习寻找路径最短的路径,而不是段数最短的那个。

• 如果是路径长度都是一样的话,那么我们进行广度优先搜索和使用我们接下来要学习的迪杰斯特拉算法,其实是差别不是很大的....起码结果都是一样的。

• 最重要的事情,要记住的是,迪杰斯特拉算法,只适用于有向无环图!!
• 迪杰斯特拉算法不适用于负权值的边

迪杰斯特拉算法(dijkstra)

我们首先来看一下我们想要走的一幅图:

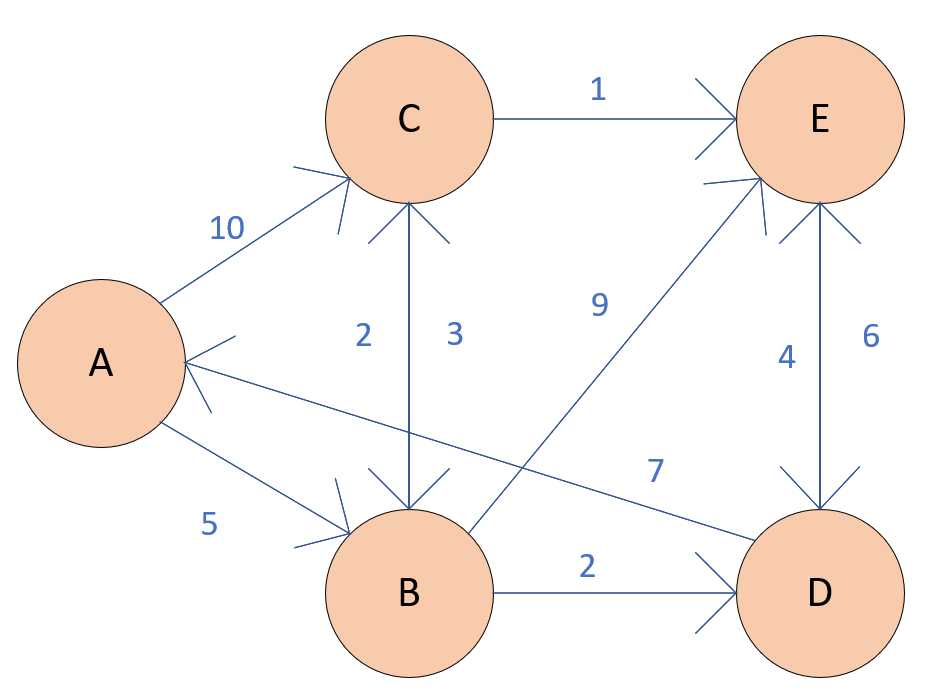
这幅图中,你可以把每个数字认为是走这条路径到另一个城市所需要的时间。然后我们要从我们的起点出发,找到一条耗时最短的路径......

其实迪杰斯特拉算法算法的主要是包含了下面的四个步骤,这是《算法图解给出的》

• 找出"最便宜"的节点,即可在最短时间内到达的节点
• 对于该节点的邻居,检查是否有前往它们的更短路径,如果有,就更新其开销
• 重复这个过程,知道对图中的每个节点都这样做了
• 计算最终路径

经过解读后,就大概是这样的.....

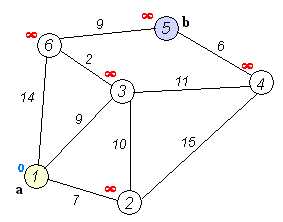
对于一幅这样的图(借鉴《算法导论》的图)来说.....

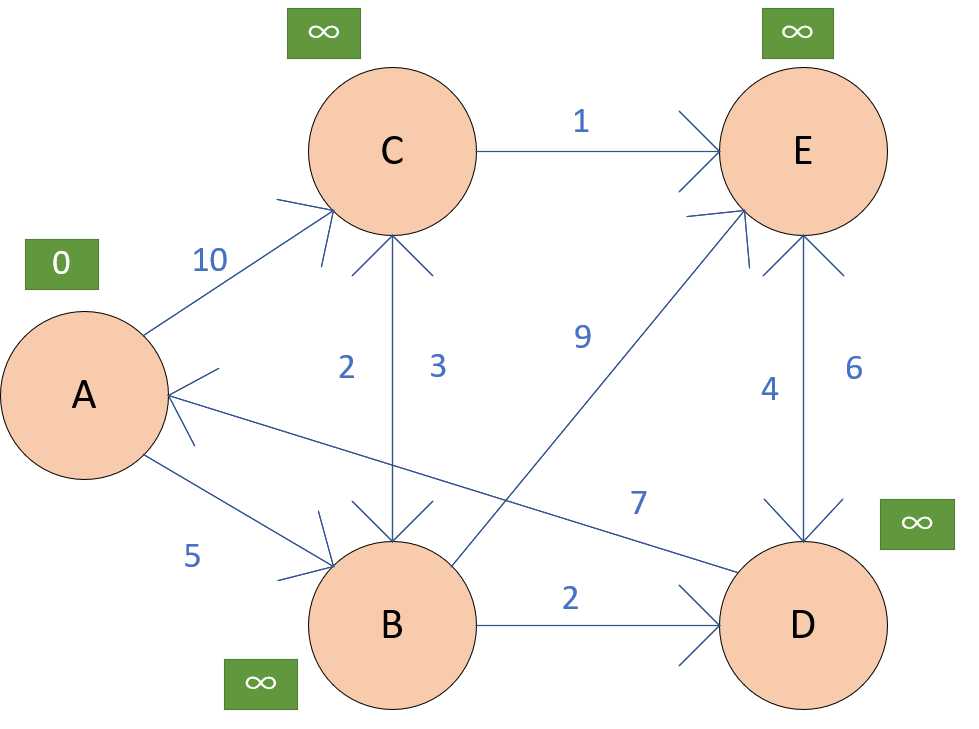
我们首先从源点出发,也就是我们图中的A点,然后从A点出发,我们寻找最小的边,也就是我们找到了从 A->B 这一条边了,然后我们把从A点到B点的距离更新,原本是无穷大,现在更新为5,同时A到C点更新为10.

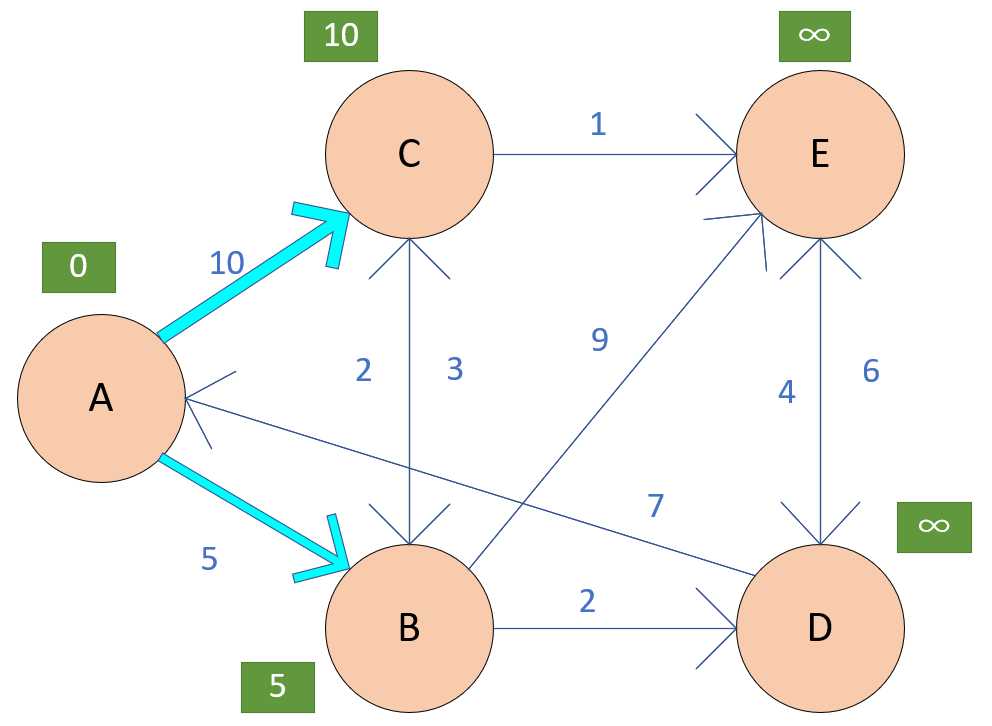
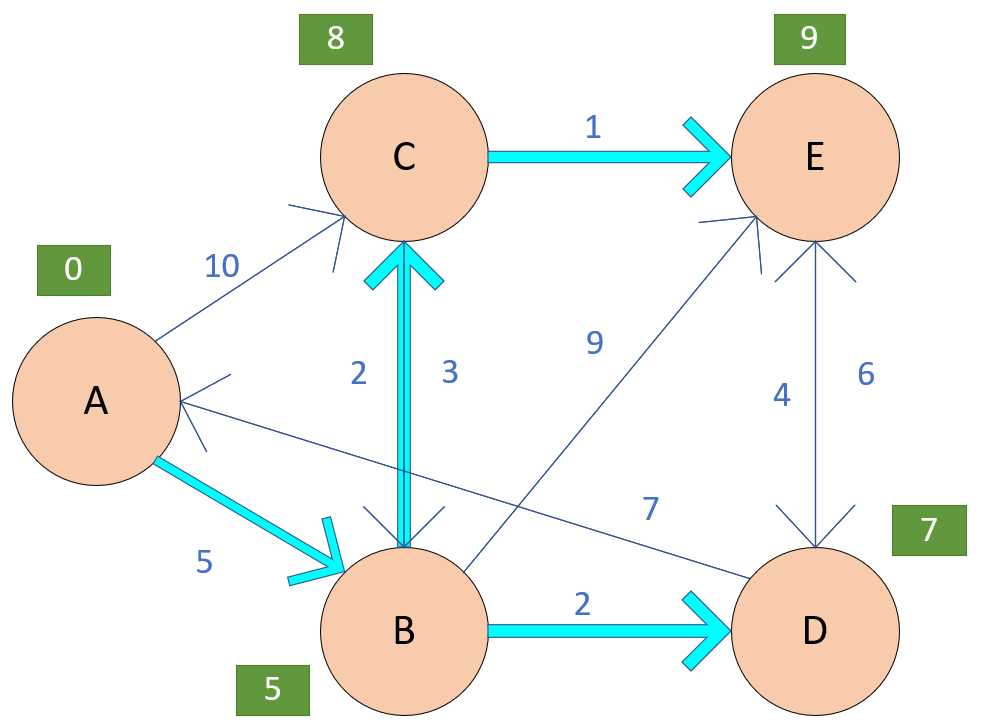
紧接着,我们选择小的那条边,到了B城市。我们在B城市中选择。从B城市可以到达C、D、E城市,那么我们相对应的给他们附上值.....

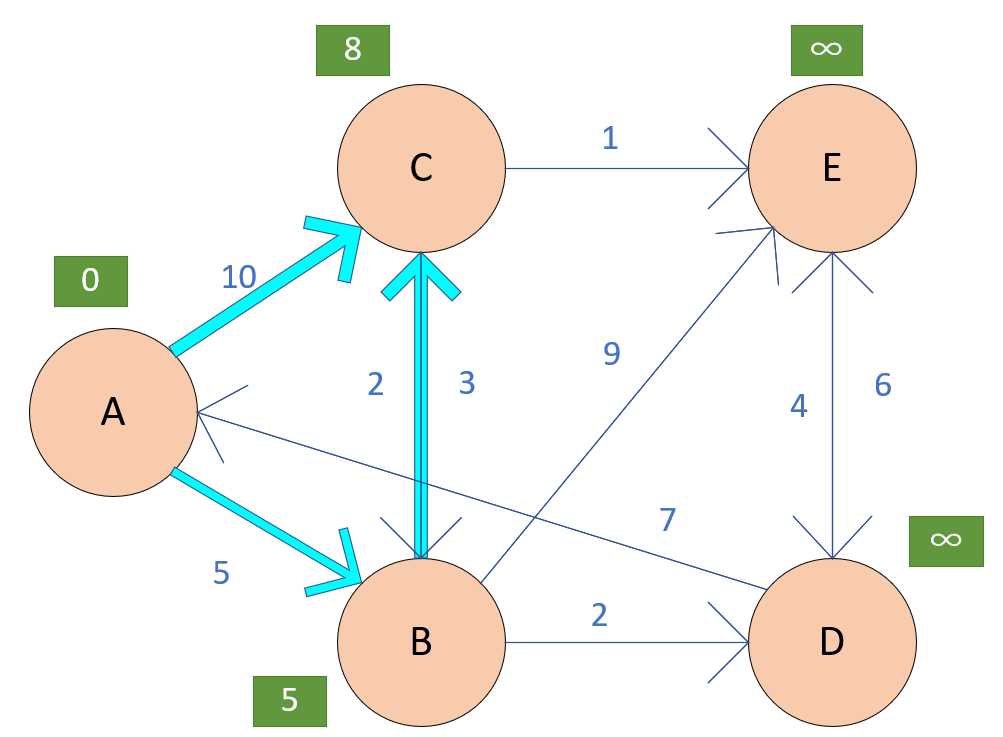
依次这样,之后我们把所有的点都更新完了.......

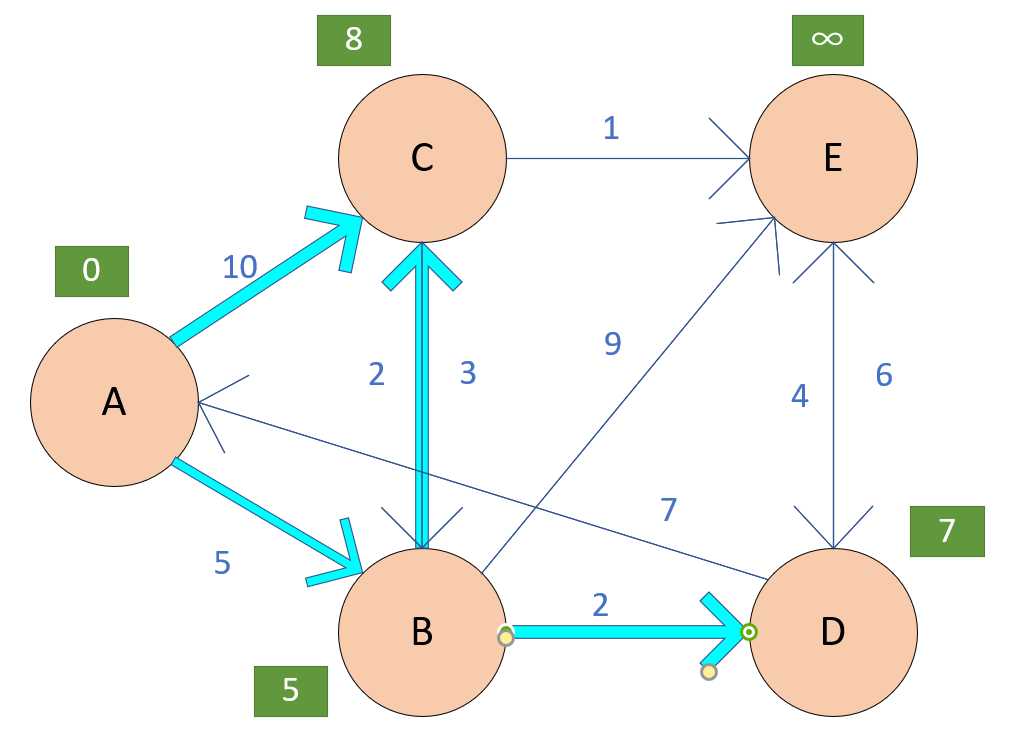
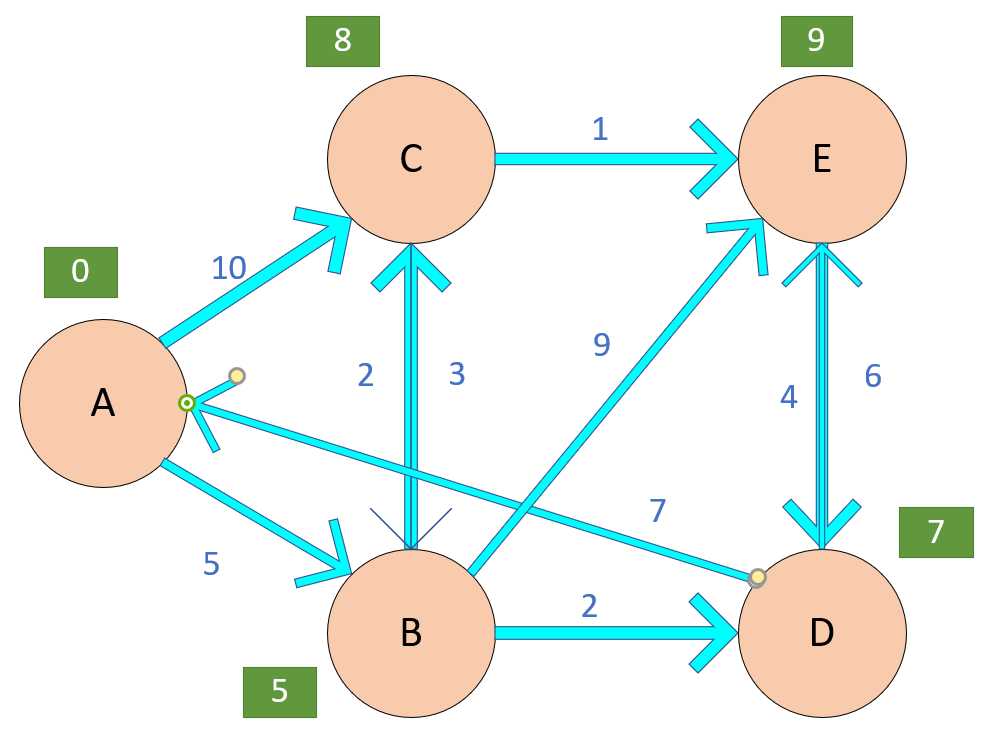
我们再来看看一个动态的图片.....

代码运行图

代码

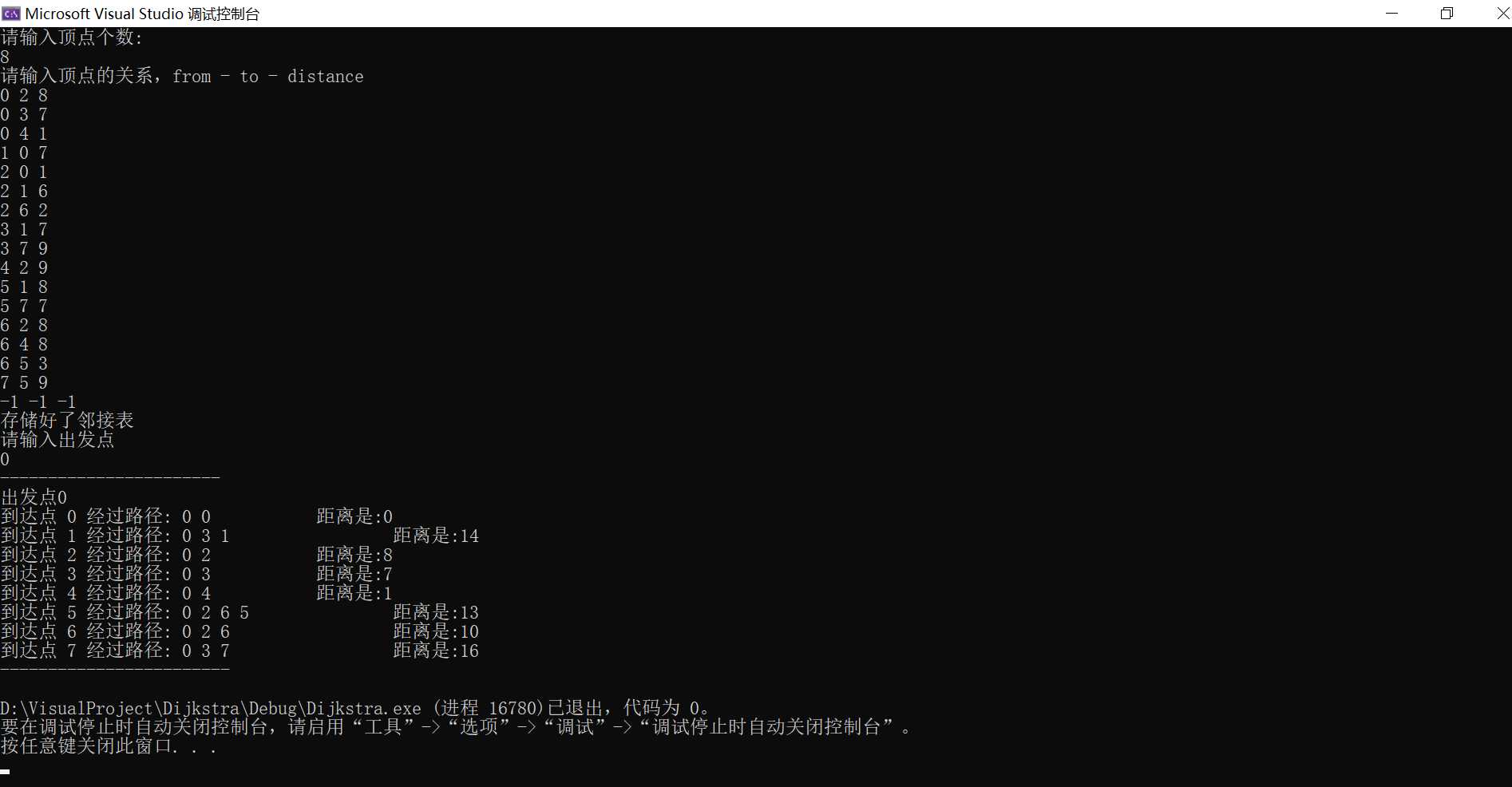
接下来到了我们学习代码的时候了( ?▽ ?)"

main.cpp

#include"Dijkstra.h"

int main()
{
    DijkstraGraph d;
    d.Init();
    d.Dijkstra();
    d.Output();
}

/*
8
0 2 8
0 3 7
0 4 1
1 0 7
2 0 1
2 1 6
2 6 2
3 1 7
3 7 9
4 2 9
5 1 8
5 7 7
6 2 8
6 4 8
6 5 3
7 5 9
-1 -1 -1
0
*/

dijkstra.h

#pragma once
#ifndef _DIJKSTRA_H_
#define _DIJKSTRA_H_
#include<iostream>
#include<cstdlib>
#include<vector>
#include<stack>
using namespace std;

struct node
{
    int to;
    int distance;
    node() {
        to = -1;
        distance = -1;
    }
};
//可以用迭代器指针去模拟
class DijkstraGraph //使用邻接表来存储
{
private:
    const int MAX = 0x3f3f3f;
    vector<vector<node>>graph;//存放图
    vector<bool>visited;
    vector<int>pre;//存放前驱
    vector<int>distance;//存放点什么到什么的距离
    int pointNumber;    
    int start;
public:
    void Init();//初始化邻接表
    void Dijkstra();//进行迪杰斯特拉算法
    void Output();//输出图示

};

#endif

dijkstra.cpp

// Dijkstra.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
#include "Dijkstra.h"

void DijkstraGraph::Init()
{
    pointNumber = 0;
    cout << "请输入顶点个数:" << endl;
    cin >> pointNumber;
    graph.resize(pointNumber );
    visited.resize(pointNumber , false);
    pre.resize(pointNumber, -1);
    distance.resize(pointNumber , MAX);
    cout << "请输入顶点的关系,from - to - distance" << endl;
    int a, b, dis;
    
    while (cin >> a >> b >> dis) 
    {
        if (a == -1 || b == -1 || dis == -1)
            break;
        node temp;
        temp.distance = dis;
        temp.to = b;
        graph[a].push_back(temp);
    }

    cout << "存储好了邻接表" << endl;
}

void DijkstraGraph::Dijkstra()
{
    vector<node>::iterator iter1;
    int start;
    int min = MAX;
    int index = 0;
    cout << "请输入出发点" << endl;
    cin >> start;
    this->start = start;
    pre[start] = 0;
    distance[start] = 0;
    
    for (int i = 0; i < pointNumber; i++)
    {
        visited[start] = true;
        //index = 0;
        min = MAX;
        for (iter1 = graph[start].begin(); iter1 < graph[start].end(); iter1++)
        {
            if (!visited[iter1->to] && distance[start] + iter1->distance < distance[iter1->to])
            {
                pre[iter1->to] = start;//进行前驱更新
                distance[iter1->to] = iter1->distance+distance[start];//距离更新
            }
        }
        for (int j = 0; j < pointNumber; j++) //找没经历过的最小的元素值
        {
            if (!visited[j] && min > distance[j])
            {
                min = distance[j];
                start = j;
            }
        }
    }
}

void DijkstraGraph::Output()
{
    stack<int>s;
    //cout << "距离:" << endl;
    //vector<int>::iterator iter;
    //for (iter = distance.begin(); iter < distance.end(); iter++)
        //cout << *iter << " ";
    int temp;
    cout << "-----------------------" << endl;
    cout << "出发点" << this->start << endl;
    for (int i = 0; i < pointNumber; i++)
    {
        cout << "到达点 " << i << " 经过路径: ";
        temp = pre[i];
        s.push(i);
        while (temp != this->start)
        {
            s.push(temp);
            temp = pre[temp];
        }
        s.push(this->start);
        while (!s.empty())
        {
            cout << s.top() << " ";
            s.pop();
        }
        cout << "\t\t 距离是:" << distance[i] << endl;

    }
    cout << "------------------------" << endl;
    
}

参考《算法图解》、《算法导论》、《数据结构与算法C语言版》

迪杰斯特拉算法 Dijkstra

原文：https://www.cnblogs.com/Yunrui-blogs/p/12088882.html