最近在看二次规划方法,对于等式约束的二次规划问题,可以使用拉格朗日方法求解。
推导方法如《最优化理论与算法(第2版)》书上所述:


这里代码如下(代码中给了三个例子):
clear all; close all; clc; % min x1^2+2*x2^2+x3^2+x2^2-2*x1*x2+x3 % s.t. x1+x2+x3 = 4 % 2*x1-x2+x3 = 2 %{ H=[2 -2 0; -2 4 0; 0 0 2]; c = [0 0 1]‘; A=[1 1 1; 2 -1 1]; b=[4 2]‘; %} %min 2*x1^2+x2^2+x1*x2-x1-x2 %s.t. x1+x2 = 1 H=[4 1; 1 2]; c=[-1 -1]‘; A=[1 1]; b=1; %min 1.5*x1^2-x1*x2+x2^2-x2*x3+0.5*x3^2+x1+x2+x3 %s.t. x1+2*x2+x3 = 4 %{ H=[3 -1 0; -1 2 -1; 0 -1 1]; c=[1 1 1]‘; A=[1 2 1]; b=4; %} invH = inv(H); S = -inv(A*invH*A‘); R = -S*A*invH; Q = invH-invH*A‘*R; x = -Q*c+R‘*b; [x1,x2]=meshgrid(0:0.02:0.7,0:0.02:1.5); z1 = 2*x1.^2+x2.^2+x1.*x2-x1-x2; mesh(x1,x2,z1); x1 = 0:0.02:0.7; x2 = -x1 + 1; hold on; plot3(x1,x2,zeros(1,length(x1)),‘r‘); plot3(x(1),x(2),0,‘r*‘) plot3(x(1),x(2),2*x(1).^2+x(2).^2+x(1).*x(2)-x(1)-x(2),‘b*‘)
结果如下:
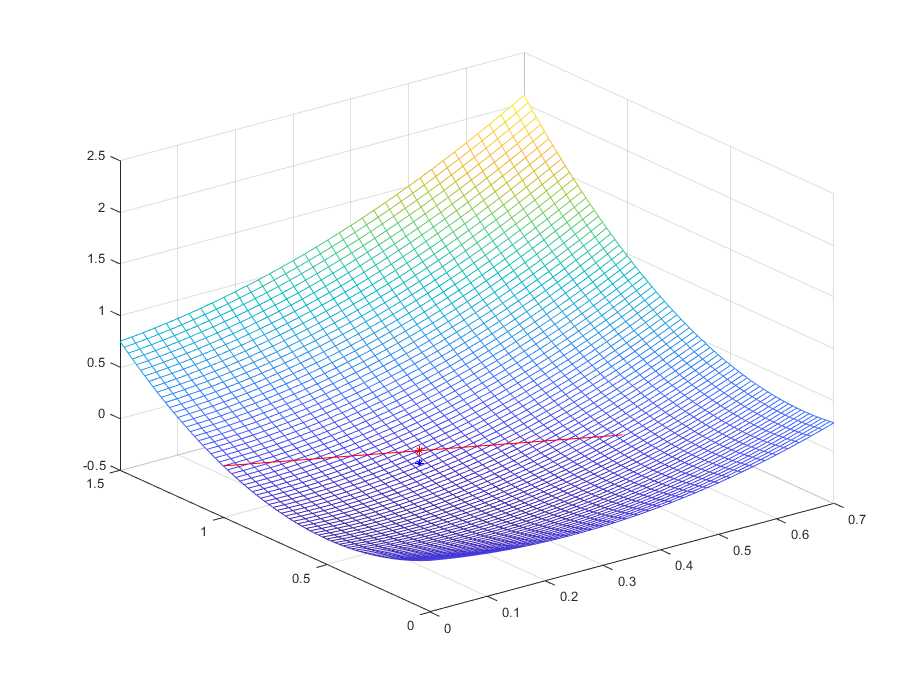
图中红线为约束条件,曲面为待求解问题函数,红点为问题的解,蓝点为二次规划问题最小值所在的位置。
原文:https://www.cnblogs.com/tiandsp/p/12088929.html