数据结构优化DP

数据结构优化DP

用途

在DP的转移中需要用到某一个阶段的最值的时候可以用线段树和树状数组等数据结构进行维护，在O(1)或O(log N) 的时间复杂度内完成转移

例题

cleaning shifts

分析

首先设计出状态，dp[x]表示从m清理到x所付出的最小代价
很显然，状态转移方程为

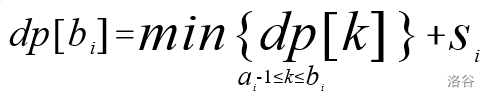
很显然，我们的每一次的转移都会用到一个区间的最小值，所以考虑运用线段树进行优化

build

我们在[m,e]上建立一颗线段树，存储DP的最小值

change

当我们更新完一个DP的值的时候，就在线段树中插入这个值

ask

每一次状态转移我们都需要在区间查找最小值

代码

#include<bits/stdc++.h>
using namespace std;

const int MAXN=1e5+5,MAXM=9e5+5;
struct Node
{
    int t1,t2,s;
}cow[MAXN];
struct node
{
    int l,r,val;
}lst[MAXM];
int n,s,e,dp[MAXM],ans;

void build_tree(int id,int l,int r)
{
    lst[id].l=l; lst[id].r=r;
    if( l==r )
    {
        lst[id].val=dp[l];
        return;
    }
    
    int mid=(l+r)/2;
    build_tree(id*2,l,mid);
    build_tree(id*2+1,mid+1,r);
    lst[id].val=min(lst[id*2].val,lst[id*2+1].val);
    return;
}

void change_tree(int id,int ver,int val)
{
    if( lst[id].l==lst[id].r )
    {
        lst[id].val=dp[ver];
        return;
    }
    
    int mid=(lst[id].l+lst[id].r)/2;
    if( mid >= ver ) change_tree(id*2,ver,val);
    else change_tree(id*2+1,ver,val);
    lst[id].val=min(lst[id*2].val,lst[id*2+1].val);
    return;
}

int ask_tree(int id,int l,int r)
{
    if( lst[id].l==lst[id].r ) return lst[id].val;
    
    int mid=(lst[id].l+lst[id].r)/2,tem=0x7f7f7f7f;
    if( mid >= l ) tem=min(tem,ask_tree(id*2,l,r));
    if( mid <= r ) tem=min(tem,ask_tree(id*2+1,l,r));
    return tem;
}

bool cmp(Node x,Node y)
{
    return x.t2 < y.t2;
}

int main()
{
    scanf("%d%d%d",&n,&s,&e);
    for(int i=1;i<=n;i++) scanf("%d%d%d",&cow[i].t1,&cow[i].t2,&cow[i].s);
    sort(cow+1,cow+n+1,cmp);
    memset(dp,0x7f7f7f7f,sizeof(dp));
    dp[s]=0;
    build_tree(1,s,e);
    for(int i=1;i<=n;i++)
    {
        int tem=ask_tree(1,cow[i].t1-1,cow[i].t2);
        dp[cow[i].t2]=tem+cow[i].s;
        if( cow[i].t2 >= e ) {ans=dp[cow[i].t2]; break;}
        change_tree(1,cow[i].t2,dp[i]);
    }
    if( ans==2139075787 ) printf("-1");
    else printf("%d",ans);
    return 0;
}

the battle of chibi

分析

实际上是给定一个长度为N的数列，求数列中有多少个长度为N的严格递增子序列
首先设计状态 dp[i] [j] 表示前j个数中以第j个数为结尾的长度为i 的严格递增序列有多少个

状态转移方程为：

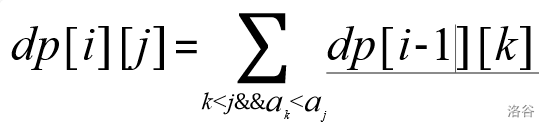
很显然，在状态转移的时候要多次用到前缀和，所以想到树状数组

数据结构优化DP

原文：https://www.cnblogs.com/BZDYL/p/12093386.html