第18章 资产收益率和风险
收益率 = 投资收益 / 投资成本
投资成本 = 资产单价 × 资产数量
期间投资收益 = 期末价格 - 期初价格 + 其他收益
期间收益率= 期间投资收益 / 期初价格
期间净收益率 = （期末价格 - 期初价格 + 其他期间收益 - 卖出交易成本）/ （期初价格+ 买入交易成本）
1. 单期简单收益率
把一段时间内每一期的资产价格按照时间先后顺序排列起来，将得到资产价格的时间序列。最早一期的价格用P1表示，之后的一期为P2，则可以得到P1,P2,...,Pt这一时间序列。投资者在t-1时刻投资某资产，投入价格为P(t-1)，持有一期后以P(t)的价格卖掉。若该资产这一期内无其他收益，也不考虑交易成本，那么投资着的单期简单收益率(One Period Simple Return)R(t)的计算公式为：
R(t) = (P(t) - P(t-1)) / P(t-1) = P(t) / P(t-1) - 1
2. 多期简单收益率
若投资者在第t-2期以价格P(t-2)购入该资产，在第t期以价格P(t)卖出。2期简单收益率计算公式为：
R(t)2 = (P(t) - P(t-2)) / P(t-2) = P(t) / P(t-2) - 1
3. 单期与多期简单收益率的关系
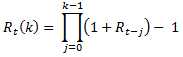
Rt (k)多期收益
Rt-j 单期收益
多期收益率的另一种算法：将单期收益率简答加总，如下：
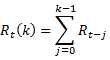
此方法得到的收益率与相乘计算得到的不同，相乘计算考虑到复利的效果；而加总计算是投入本金之后，每一期获得的收益没有再投入到资产中的收益。
由多期收益率计算单期收益率涉及到平均的概念，计算的是在过去持有资产的几期里，平均每期的收益是多少。有两种方式，一种是算术平均(Arithmetric Average)，另一种是几何平均(Geometric Average)。
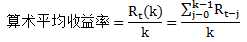
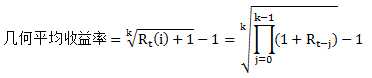
几何平均有考虑复利，衡量的是过去k期中将每期的收益作为本金投入下期资产中的这种投资方法的平均收益，算术平均没有考虑复利的效果。
4. 年化收益
年化收益的计算与复利有关，假设投资人持有资产的时间为T期，获得的收益率为RT ，一年一共有m个单期，则该资产的年化收益率为：
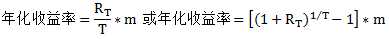
其中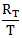
是根据T期收益计算的算术平均收益率，
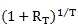是几何平均收益率，之后将单期收益率转化成年化收益时是直接乘以一年的期数m，也就是将单期行为复制m次得到的收益率。
5. 考虑股利分红的简单收益率
现金股利是公司将盈余以现金的方式发放给股东，而股票股利则是用送股的方式，将股票发给股东。
只有在股权登记日之前（包含股权登记日这一天）持有公司股票的股东才有权分享股利。
a)除息价：
除息价 = 股息登记日的收盘价 - 每股红利现金金额
b）除权价：
送红股后的除权价 = 股权登记日的收盘价 / （1 + 每股送红股数或转增股数）
c）除权除息价：
除权除息价 = （股权登记日的收盘价 - 每股红利现金额） / （1 + 每股送红股数或转增股数）
股息率 = 股息 / 股票价格 × 100%
市盈率 = 每股市价 / 每股盈利 （每股盈利一般是以公司在过去一年的净利润除以总发行已售出股数。）
6. 资产风险的测度
（1）方差
金融资产的风险用该资产收益的不确定性来度量，即方差风险度量方法：
单个资产的风险具体可以表达为：
其中R为有可能发生的收益率，E(R)为期望收益率。
（2）下行风险
计算下行偏差时，一个最重要的变量就是目标收益率，通常用可接受的最低收益率(Minimum Acceptable Rate of Return, MARR)代表，MARR可以是无风险收益率，或者0，或者资产收益率的平均值。
用下行偏差描述的风险被称为下行风险(Downside Risk)。
（3）风险价值
风险价值(Value at Risk, VaR)是给定的置信水平和目标时段下预期的最大损失。即在市场正常波动的条件下，，在一定概率水平α%下，某一金融资产或金融资产组合的VaR(α, Δt)是在未来特定的一段时间Δt内的最大可能损失，用数学公式表达为：
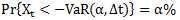
VaR将风险以具体的数字表现出来，使投资者能够清晰直观地认识到风险的大小程度；并且投资者可以通过设置不同的置信区间和评估区间管理风险。
第20章 资本资产定价模型（CAPM）
对于任意的资产组合q，其收益率Rq 满足一下关系式：
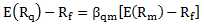
Rm 是市场投资组合之收益率，该组合是市场上所有风险资产的组合，包括股票等金融资产，也包括黄金等实物资产。实际上以大盘指数来指代市场投资组合。
为投资组合q的Beta值，其中
为资产组合收益率与市场投资组合收益率之间的协方差，
为市场投资组合的方差，Beta值反映出资产组合q的系统性风险。
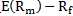为风险投资组合q比无风险资产高出的期望收益率，搞出来的部分是因为投资人在持有风险组合q时承担了更多的风险，因此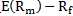被称为风险溢酬（Risk premium）。
原文：https://www.cnblogs.com/sssblog/p/12103576.html