- 事实上,”带正则项”和“带约束条件”是等价的。
-
为了约束w的可能取值空间从而防止过拟合,我们为该最优化问题加上一个约束,就是w的L1范数不能大于m:
{min∑Ni=1(wTxi−yi)2s.t.∥w∥1?m.........(3){min∑i=1N(wTxi−yi)2s.t.‖w‖1?m.........(3)
- 问题转化成了带约束条件的凸优化问题,写出拉格朗日函数:
∑i=1N(wTxi−yi)2+λ(∥w∥1−m)........(4)∑i=1N(wTxi−yi)2+λ(‖w‖1−m)........(4)
-
设W∗W∗和λ∗λ∗是原问题的最优解,则根据KKTKKT条件得:
{0=∇w[∑Ni=1(WT∗xi−yi)2+λ∗(∥w∥1−m)]0?λ∗.........(5){0=∇w[∑i=1N(W∗Txi−yi)2+λ∗(‖w‖1−m)]0?λ∗.........(5)
- 仔细看上面第一个式子,与公式(1)其实是等价的,等价于(3)式。
- 设L1正则化损失函数:J=J0+λ∑w|w|J=J0+λ∑w|w|,其中J0=∑Ni=1(wTxi−yi)2J0=∑i=1N(wTxi−yi)2是原始损失函数,加号后面的一项是L1正则化项,λλ是正则化系数。
- 注意到L1正则化是权值的绝对值之和,JJ是带有绝对值符号的函数,因此JJ是不完全可微的。机器学习的任务就是要通过一些方法(比如梯度下降)求出损失函数的最小值。当我们在原始损失函数J0J0后添加L1正则化项时,相当于对J0J0做了一个约束。令L=λ∑w|w|L=λ∑w|w|,则J=J0+LJ=J0+L,此时我们的任务变成在LL约束下求出J0J0取最小值的解。
- 考虑二维的情况,即只有两个权值w1w1和w2w2,此时L=|w1|+|w2|L=|w1|+|w2|对于梯度下降法,求解J0J0的过程可以画出等值线,同时L1正则化的函数LL也可以在w1w1、w2w2的二维平面上画出来。如下图:
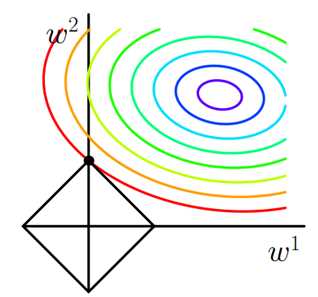
- 上图中等值线是J0J0的等值线,黑色方形是LL函数的图形。在图中,当J0J0等值线与LL图形首次相交的地方就是最优解。上图中J0J0与LL在LL的一个顶点处相交,这个顶点就是最优解。注意到这个顶点的值是(w1,w2)=(0,w2)(w1,w2)=(0,w2)。可以直观想象,因为LL函数有很多突出的角(二维情况下四个,多维情况下更多),J0J0与这些角接触的机率会远大于与LL其它部位接触的机率,而在这些角上,会有很多权值等于00,这就是为什么L1正则化可以产生稀疏模型,进而可以用于特征选择。
-
而正则化前面的系数λλ,可以控制LL图形的大小。λλ越小,LL的图形越大(上图中的黑色方框);λλ 越大,LL的图形就越小,可以小到黑色方框只超出原点范围一点点,这是最优点的值(w1,w2)=(0,w2)(w1,w2)=(0,w2)中的w2w2可以取到很小的值。
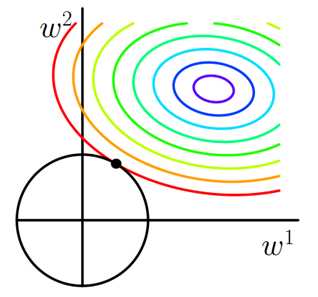
- 同理,又L2正则化损失函数:J=J0+λ∑ww2J=J0+λ∑ww2,同样可画出其在二维平面的图像,如下:
-
二维平面下L2正则化的函数图形是个圆,与方形相比,被磨去了棱角。因此J0J0与LL相交时使得w1w1或w2w2等于零的机率小了许多,这就是为什么L2正则化不具有稀疏性的原因。


