样本空间是一个随机试验所有可能结果组成的集合。
例如抛掷一枚硬币,那么样本空间就是集合{正面,反面}。
例如投掷一个骰子,那么样本空间就是集合{1,2,3,4,5,6}。
随机试验中的每个可能结果称为样本点或基本事件。样本空间又叫基本事件空间
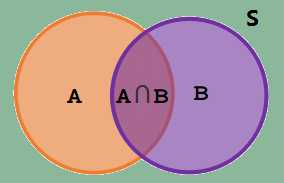
如上图,假设有一个样本空间S,里面分别包括子样本空间A和子样本空间B,A∩B是两个样本空间的交集。
P(A) = P(A|S) = 样本空间A所含样本点数 / 样本空间S所含样本点数
P(B) = P(B|S) = 样本空间B所含样本点数 / 样本空间S所含样本点数
P(AB) = P(AB|S) = 样本空间A∩B所含样本点数 / 样本空间S所含样本点数
先说P(AB),其中的AB即为A和B两个空间相交的部分A∩B,这部分也可以视为在B空间上A也出现了(或在A空间上B也出现了),其实这个公式P(AB)是以S为样本空间的
再看P(A|B)或P(B|A),满足这个公式的前提是A和B一定有交集
P(A|B) = 样本空间B中出现A的样本点数 / 样本空间B所含样本点数 = P(AB) / P(B)
P(B|A) = 样本空间A中出现B的样本点数 / 样本空间A所含样本点数 = P(AB) / P(A)
因此,条件概率公式为:
原文:https://www.cnblogs.com/cwfj/p/12100663.html