这次练习主要针对的是“回溯法”
简单介绍一下,回溯法->深度优先搜索算法->dfs(Depth First Search)
所以个人习惯上都是对于任何需要回溯的问题,其函数命名为dfs。
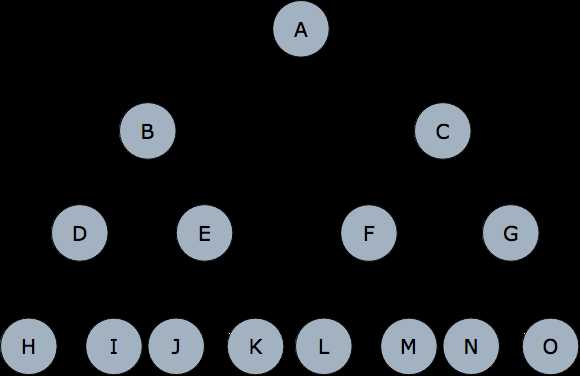
深度优先搜索,本质上是对一颗搜索树进行搜索。
相较于BFS来说,DFS搜索顺序为“找到一个节点一直叶子结点”
BFS和DFS两者之间:
1、dfs相较于bfs比较方便好使,因为过程不借助队列
2、如果同一个问题用bfs和dfs都能实现情况下,通常用bfs,
原因有:搜索空间一定的情况下,dfs比bfs多了一步回溯的操作。
例如迷宫问题明显时BFS优势大。
对于期末考试考查以下三种能力
1、子集树(01背包问题,幻方数)
2、排列树(TSP问题)
3、类多叉树遍历(李白打酒,n皇后)
顾名思义,利用集合的思路进行操作。
集合有三种性质,(无序性,互异性,确定性)
在求解过程中,利用更多的是“互异性” (即集合中不存在两个相同的元素)。
问题描述:
对于给定一个背包,其背包有一定的承重能力,给出有n个物品,物品以<value,weight>形式出现。
请问在背包承重范围内,实现背包的最大价值。
题解:
假定 每个物品“取和不取” => 取 <-> ‘1‘ 不取 <-> ‘0‘
然后对于3个物品的背包问题共有2^3=8种情况,如下所示
(000) -> {}
(001) -> {1}
(010) -> {2}
(011) -> {1,2}
(100) -> {3}
(101) -> {1,3}
(110) -> {2,3}
(111) -> {1,2,3}
由于集合的互异性,每次在物品放与不放时,都需要判断当前集合中是否存在物品。
我们需要借助一个标记数组来进行操作
标记数组名可以为“vis(visit)” , "book" , "st(state)" , "used"
问题转化为:构建一颗搜索树,高度为n层,每一个节点都表示背包状态,
同时每一层都是表示物品放和不放,若走左子树<->物品放,否则走右子树<->物品不放。

1 //dfs子集树解决01背包问题 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 const int N = 5; 6 ? 7 int value[] = { 45 , 25 , 25 }; 8 int weight[] = { 16 , 15 , 15 }; 9 int V = 30 ; 10 ? 11 int n = 3 ; //物品数量 12 int ans ; //答案 13 int val , w ; //每个结点中<value,weight>的状态 14 int vis[N] ; //物品标记状态 15 ? 16 void dfs( int step ){ 17 ? 18 //到达叶子结点 19 if( step == n ){ 20 ans = max( ans , val ); 21 return ; 22 } 23 ? 24 //物品不在背包中,且放物品后还在背包承受范围内. 25 if( vis[step] == 0 && w + weight[step] <= V){ 26 //对于第Step个物品进行标记,同时更新结点对应的<val,w>状态 27 vis[step] = 1 ; 28 w += weight[step] ; 29 val += value[step] ; 30 ? 31 //往左子树走 32 dfs( step + 1 ); 33 ? 34 //回溯,返回结点后需要把第step个物品取出来, 35 //同时恢复 结点对应的<val,w>状态 36 val -= value[step] ; 37 w -= weight[step] ; 38 vis[step] = 0 ; 39 } 40 //往右子树走 41 dfs( step + 1 ); 42 } 43 ? 44 int main() 45 { 46 dfs(0) ; 47 printf("%d\n",ans); 48 return 0 ; 49 }
结点状态<value,weight>如果用全局变量表示比较复杂。
但如果用函数参数来表示当前结点状态则清爽很多。

1 //dfs子集树解决01背包问题 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 const int N = 5; 6 ? 7 int value[] = { 45 , 25 , 25 }; 8 int weight[] = { 16 , 15 , 15 }; 9 int V = 30 ; 10 ? 11 int n = 3 ; //物品数量 12 int ans ; //答案 13 int vis[N] ; //物品标记状态 14 ? 15 void dfs( int step , int val , int w ){ 16 ? 17 //到达叶子结点 18 if( step == n ){ 19 ans = max( ans , val ); 20 return ; 21 } 22 23 //物品不在背包中,且放物品后还在背包承受范围内. 24 if( vis[step] == 0 && w + weight[step] <= V){ 25 vis[step] = 1 ; 26 dfs( step + 1 , val + value[step] , w + weight[step] ); 27 vis[step] = 0 ; 28 } 29 //往右子树走 30 dfs( step + 1 , val , w ); 31 } 32 ? 33 int main() 34 { 35 dfs(0,0,0) ; 36 printf("%d\n",ans); 37 return 0 ; 38 }
排列树顾名思义,还是以排列(permutation)为基础。
解决的问题是:通常以全排列为基础的题目。
1,2,3的全排列:
123 , 132 , 213 , 231 , 312 , 321
譬如求解数字排列问题;或者以全排列的基础的问题。
【问题描述】
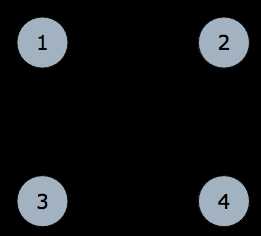
旅行商问题,即TSP问题(Traveling Salesman Problem)又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
【题解】
TSP问题是一个著名的NP问题,目前没有找到一个有效的算法,只能通过穷举方式来算。这里用的穷举就是用全排列来实现,答案必定是n!种排列中的一种,我们就算出n!取其最小值的那个即可。
算法实现过程主要涉及到:
利用交换实现排列顺序中“谁打头”,然后其余的排列就是在后面的位置进行交换。
大家在草稿纸上自己写一下:1,2,3,4的全排列
1234,1243,1324,1342,1432,1423……
2***,……
3***,……
4***,……
(共24种情况)
我们在自己写的过程也是注重‘顺序’。
这个顺序是针对4个位置,固定前几个,然后交换后面几个顺序。
其实这个排列树就是和我们手写时侧重的思路是相符的。
这一过程其实是:固定n个位置,每一个位置放数字,
在一个排列中,通过交换方式实现每个数字都在该位置放置过。同时为了达到不重不漏,下一个位置还是进行相应的操作。

设计函数
设置两个游标卡住数组的一个范围 ->指的是对该部分[ start , end ]进行全排列。
当两个游标指到同一个位置时:也就是到达了叶子结点。
如果还未到叶子结点,此过程必须要进行交换,当前位置其实是:S,交换的下标为[S,E]。
注意: 这里是[S,E],而不是[S+1,E],因为S这个位置本身也是作为一种排列。
举例:‘1’,2,3,4,此时在第一个位置进行枚举,若[S+1,E]
就会出现,‘2‘,1,3,4 , ‘3‘,2,1,4 , ‘4‘,2,3,1 却少了‘1‘,2,3,4
每一个位置都进行相应的操作,就能实现全排列。

1 //dfs子集树解决TSP问题 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 const int N = 5; 6 ? 7 //邻接矩阵 8 int dis[N][N] = { 9 0 , 0 , 0 , 0 , 0 , 10 0 , 0 , 30, 6 , 4 , 11 0 , 30, 0 , 5 , 10, 12 0 , 6 , 5 , 0 , 20, 13 0 , 4 , 10, 20, 0 14 }; 15 //人为设定dis[][]下标是由1开始的,所有dis[0][j] 和 dis[i][0]都为0 16 ? 17 // permutation : 排列方式,排列数 18 int perm[] = { 0 , 1 , 2 , 3 , 4 };//令其下标为1开始 19 int path[N] ; 20 int n = 4 ; //城市个数 21 int ans = 1e6; //答案,初始化一个很大的数 22 ? 23 void dfs( int S , int E ){ // Start , End 24 if( S == E ){ 25 /* 26 显示所有排列方式 27 for( int i = 1 ; i <= n ; i++ ){ 28 printf("%3d",perm[i],i==n?‘\n‘:‘ ‘); 29 } 30 putchar(‘\n‘); 31 */ 32 //计算其该排列顺序的代价 33 int tmp = 0 ; 34 for( int i = 2 ; i <= n ; i++ ){ 35 tmp += dis[perm[i]][perm[i-1]]; 36 } 37 //更新其答案,并记录当前的路径 38 if( tmp < ans ){ 39 for( int i = 1 ; i <= n ; i++ ){ 40 path[i] = perm[i] ; 41 } 42 ans = tmp ; 43 } 44 return ; 45 } 46 for( int i = S ; i <= E ; i++ ){ 47 swap( perm[S] , perm[i] ); 48 dfs( S + 1 , E ) ; 49 swap( perm[S] , perm[i] ); 50 } 51 } 52 ? 53 int main() 54 { 55 dfs( 1 , 4 ) ; 56 printf("%d\n",ans); 57 for( int i = 1 ; i <= n ; i++ ){ 58 printf("%-2d",path[i]); 59 } 60 putchar(‘\n‘); 61 return 0 ; 62 }
话说大诗人李白,一生好饮。幸好他从不开车。一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱: 无事街上走,提壶去打酒。 逢店加一倍,遇花喝一斗。 这一路上,他一共遇到店5次,遇到花10次,已知最后一次遇到的是花,他正好把酒喝光了。 请你计算李白遇到店和花的次序,可以把遇店记为a,遇花记为b。则:babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢?请你计算出所有可能方案的个数(包含题目给出的)。
李白打酒这类问题,本质问题其实也是一棵搜索树,这棵树进行遍历,李白走到某一位置时相当于走到搜索树哪一层,同时每个节点往上看都说明李白之前encounter 店和花的数量 和 酒壶中的酒的量。针对该问题:我们可以得知它时二叉树,因为李白走下一个位置只有花和店两种情况。每个节点都是一个<flower,shop,wine>的三元组。
往左子树走时,我们定义为遇到酒店,<flower,shop+1,wine*2>
往右子树走时,我们定义为遇到花朵,<flower+1,shop,wine-1>
我们这颗搜索树就是只有flower+shop层。如例子中,5+10=15层,叶子结点就是flower=5,shop=10.
问题就转化成 :到达二叉树的15层后,叶子结点<flower==5,shop==10,wine==0>的情况。输出李白在途中所遇到的店和花的排列问题,也就是遍历二叉树的问题。

1 //dfs解决李白打酒问题 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 const int N = 20 ; 6 char path[N] ; 7 int cnt = 0 ; 8 void dfs( int step , int shop , int flower , int wine ){ 9 if( step == 15 && shop == 5 && flower == 10 && wine == 0 ){ 10 for( int i = 0 ; i < step ; i++ ){ 11 printf("%c",path[i]); 12 } 13 putchar(‘\n‘); 14 cnt ++ ; 15 return ; 16 } 17 // 若走左子树,已遇到酒店的数量不超过5,同时过程中不能出现酒为0 18 // 因为 若不加以判断,酒为0时 0 * 2 = 0 ,明显是不合法的 19 if( shop < 5 && wine >= 1 ){ 20 path[step] = ‘a‘ ; 21 dfs( step + 1 , shop + 1 , flower , wine * 2 ); 22 } 23 // 若走右子树,已遇到花的数量不超过10, 同时酒壶也必须有酒 24 if( flower < 10 && wine >= 1 ){ 25 path[step] = ‘b‘ ; 26 dfs( step + 1 , shop , flower + 1 , wine - 1 ); 27 } 28 ? 29 } 30 int main() 31 { 32 dfs( 0 , 0 , 0 , 2 ); 33 printf("%d\n",cnt); 34 return 0 ; 35 }
N个国际象棋的皇后,放置在N*N的棋盘,使其相互之间不能攻击到对方。
皇后的攻击范围:所在行,所在列,所在两个对角线。
请问有多少种情况。
【题解】
N皇后是经典的题目,对于搜索来说,可以是过程中利用标记数组,同时还需要判断过程是否合法。
我们搜素顺序是按照列的顺序,然后每一列中我们把皇后放在第i行中。
实际该问题类似n叉树,但是n叉树会随着搜索树往下而减少。
第一层是n叉树,第二层每一个结点 都是 n-1叉树……

1 //dfs解决N皇后问题 2 ? 3 #include<cstdio> 4 #include<cstdlib> 5 const int N = 50 ; 6 int vis[N] , Queen[N] ; 7 ? 8 //判断放置在x列的皇后是否合法 9 bool check( int x ){ 10 for( int i = 1 ; i < x ; i++ ){ 11 if( abs( x - i ) == abs( Queen[x] - Queen[i] ) ){ 12 return false ; 13 } 14 } 15 return true ; 16 } 17 ? 18 int n = 8 ; 19 int ans = 0 ; 20 ? 21 void dfs( int step ){ 22 if( step == n + 1 ){ 23 ans ++ ; 24 return ; 25 } 26 for( int i = 1 ; i <= n ; i++ ){ 27 //当前行没被占据 28 if( vis[i] == 0 ){ 29 //把皇后 放置在 <第i行,第step列> 30 Queen[step] = i ; 31 ? 32 //判断其是否合法,若合法继续搜索 33 if( check(step) ){ 34 //往下深搜时,记得打标记. 35 vis[i] = 1 ; 36 dfs( step + 1 ); 37 //回溯使记得撤标. 38 vis[i] = 0 ; 39 } 40 } 41 } 42 } 43 int main() 44 { 45 dfs( 1 ) ; 46 printf("%d\n",ans); 47 return 0; 48 }
幻方是把一些数字填写在方阵中,使得行、列、两条对角线的数字之和都相等。欧洲最著名的幻方是德国数学家、画家迪勒创作的版画《忧郁》中给出的一个4阶幻方。 他把1,2,3,...16 这16个数字填写在4 x 4的方格中。 16 ? ? 13 ? ? 11 ? 9 ? ? * ? 15 ? 1 表中有些数字已经显露出来,还有些用?和*代替。
根据幻方的定义,对于方格进行搜索,过程中借助标记数组。
然后搜素到最后利用幻方的定义判断是否都行列对角线是否符合幻方要求。

1 //dfs解决幻方数 2 ? 3 /* 4 16 ? ? 13 5 ? ? 11 ? 6 9 ? ? * 7 ? 15 ? 1 8 */ 9 ? 10 #include<cstdio> 11 ? 12 const int N = 20 ; 13 const int M = 5 ; 14 int magic[M][M] , n = 4 ; 15 int row[M] , col[M] , diag[2] ; 16 int vis[N] ; 17 ? 18 void Init(){ 19 magic[1][1] = 16 ; magic[1][4] = 13 ; 20 magic[2][3] = 11 ; magic[3][1] = 9 ; 21 magic[4][2] = 15 ; magic[4][4] = 1 ; 22 //vis[*] = -1 固定着,不让其修改 23 vis[1] = vis[9] = vis[11] = vis[13] = vis[15] = vis[16] = -1 ; 24 ? 25 //设定行列对角线的初始值 26 row[1] = 29 ; row[2] = 11 ; row[3] = 9 ; row[4] = 16 ; 27 col[1] = 25 ; col[2] = 15 ; col[3] = 11 ; col[4] = 14 ; 28 ? 29 diag[0] = 17 ; diag[1] = 24 ; 30 } 31 ? 32 //遍历顺序是从左往右,从上到下 33 void dfs( int x ,int y ){ 34 ? 35 //到达最后一个格子,因为最后一个位置已固定,所以直接计算即可 36 if( x == n && y == n ){ 37 int tmp = 0 ; 38 for( int i = 1 ; i <= n ; i++ ){ 39 tmp += (row[i]==34) ; 40 tmp += (col[i]==34) ; 41 } 42 tmp += ( diag[0] == diag[1] && diag[0] == 34 ); 43 ? 44 if( tmp == 9 ){ 45 for( int i = 1 ; i <= n ; i++ ){ 46 for( int j = 1 ; j <= n ; j ++ ){ 47 printf("%-3d",magic[i][j]); 48 } 49 putchar(‘\n‘); 50 } 51 } 52 return ; 53 } 54 if( vis[magic[x][y]] == -1 ){ 55 if( y == n ){ 56 dfs( x + 1 , 1 ); 57 }else{ 58 dfs( x , y + 1 ); 59 } 60 } 61 else{ 62 //因为1,15,16都已在幻方中,所以直接搜索[2,14] 63 for( int i = 2 ; i <= 14 ; i++ ){ 64 //当前这个数字没有被用过 65 if( vis[i] == 0 ){ 66 vis[i] = 1 ; 67 magic[x][y] = i ; 68 ? 69 //添加后修改该行列对角线的总和 70 row[x] += i ; 71 col[y] += i ; 72 diag[0] += (x==y) * (i); 73 diag[1] += (x==n+1-y) * (i) ; 74 ? 75 //往下走,如果到最右边,则换行 76 if( y == n ){ 77 dfs( x + 1 , 1 ); 78 }else{ 79 dfs( x , y + 1 ); 80 } 81 82 //记得撤出标记 83 vis[i] = 0 ; 84 row[x] -= i ; 85 col[y] -= i ; 86 diag[0] -= (x==y) * (i); 87 diag[1] -= (x==n+1-y) * (i) ; 88 } 89 } 90 } 91 } 92 int main(){ 93 Init() ; 94 dfs( 1 , 1 ); 95 return 0; 96 }
原文:https://www.cnblogs.com/Osea/p/12111476.html