讲授聚类算法的基本概念,算法的分类,层次聚类,K均值算法,EM算法,DBSCAN算法,OPTICS算法,mean shift算法,谱聚类算法,实际应用
课程大纲:
基于密度的聚类算法简介
DBSCAN算法的核心思想
基本概念定义
算法的流程
实现细节问题
实验
OPTICS算法的核心思想
基本概念定义
算法的流程
根据排序结果生成聚类结果
实验
Mean Shift算法的核心思想
核函数概率密度估计
算法的流程
谱聚类算法的核心思想
基本概念定义
算法的流程
算法评价指标
应用
聚类算法总结
这节课讲,基于密度的聚类算法:DBSCAN算法、OPTICS算法、Mean Shift算法,然后讲谱聚类算法,然后讲算法评价指标及应用,然后为这两节课做一个总结。
基于密度的聚类算法简介:
它就是算空间中所有地方的样本点的密度,分布比较密集的样本点就认为是一个类,其他的分布不密集的地方的样本点就认为是噪声点。因此它的聚类依赖于空间中每个样本点处样本的密度,如果比较密的话可能就是一个簇否则就不是一个簇。这个算法有一个好处是,它可以找出形状不规则的簇,因为它没有中心,它不定义中心点,不像kmeans、高斯混合模型那样的算法它需要计算中心向量,因此kmeans、高斯混合模型那样的算法比较倾向于聚类那种比较圆的球状椭球状分布的类,而这类算法呢,它可以发现任何形状的类,只要是联通的,比如说S型拐弯的、带状分布、卷曲的,它都是能处理的。它还有一个好处是,不用指定类的数量簇的数量不用人工指定,不像k均值算法一样要先设定一个k值。这种算法最核心的一步是计算每个样本点处的密度值,以及根据密度值来构造出簇,一般的做法是从一个比较密的点我们称为核心点反复的开始伸展开始扩张,扩展到样本比较稀疏的地方去,把那个地方围起来,这就是一个簇。
根据样本点某一邻域内的邻居数定义数据空间的密度,这类算法可以找出空间中形状不规则的簇,不用指定簇的数量。
算法的核心是计算密度值,以及根据密度来定义簇。
DBSCAN算法的核心思想:
第一种基于密度的聚类算法,经典的DBSCAN算法。
Martin Ester, Hanspeter Kriegel, Jorg Sander, Xu Xiaowei. A density-based algorithm for discovering clusters in large spatial databases with noise. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, pp. 226–231, 1996.
它是最简单的一种基于密度的聚类算法,它的核心思想前边已经说了,就是通过先计算所有样本点处空间分布的密度,然后从某个种子样本开始找,如果这个点是个核心点很密集的话,就反复的往外伸展一直到边界处我们就成了一个簇,找完一个簇之后再找另外一个种子点继续下一个簇,知道把所有的样本处理一遍以后,这个算法就就结束了。
这种算法对噪声非常鲁棒,因为它天然可以发现各种噪声,所有的噪声样本点它可以把它剔除掉,不会聚到簇里边去,这是高斯混合模型、EM算法、k均值算法等等这些算法不能比拟的一个优势。
它将簇定义为样本密集的区域,算法从一个种子样本开始,反复向密集的区域生长,直至到达边界,所谓边界就是再往外走样本就很稀疏了,再往里走分布就很密集了,到达这样的点处我们就得到一个簇了。
基本概念定义:
这个算法依赖于一些基本的概念,下面介绍一下这些概念。
核心点:
邻居数量大于指定阈值的样本点。

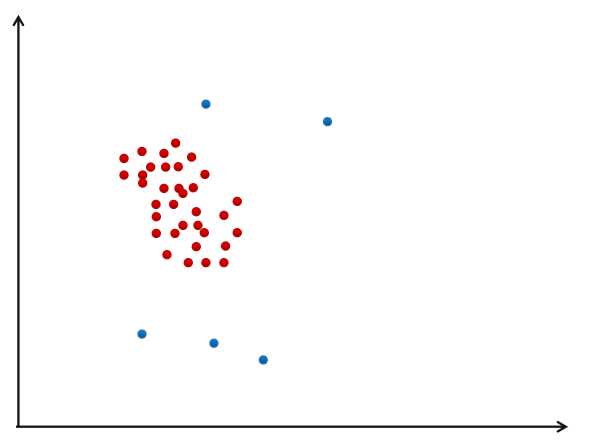
如图,如果M设置为5的话,靠近中间的红点是核心点,红色区域边界和蓝色的点都不是核心点。
所有核心点构成的集合记为:Xc,c是core的简写。
所有非核心点构成的集合记为:Xnc。
如果一个点不是核心点,但在它的邻域内有核心点,则称该点为边界点。核心点和边界点都是我们在聚类的时候的目标,就是每个簇里边包含核心点也包含边界点。
如果一个点既不是核心点,也不是边界点,则称为噪声点。
如果x是核心点,y在它的邻域内,则称y是从x直接密度可达的。
对于一组样本x1,...,xn,如果xi+1是从xi直接密度可达的,则称xn是从x1密度可达,这里xn之前的所有的点要是核心点,而xn不一定是核心点。
对于x,y,z,如果y和z都从x密度可达,则称y和z密度相连。
有了密度可达和密度相连以后,就可以定义一个簇了:
假设C是整个样本集X的一个子集,如果满足:对于样本集X中中任意两个样本x和y,如果x∈C,且y是从x密度可达的,则y∈C,如果x∈C,y∈C,则x和y是密度相连的,则称集合C为一个簇。
再来回顾一下密度可达和密度相连: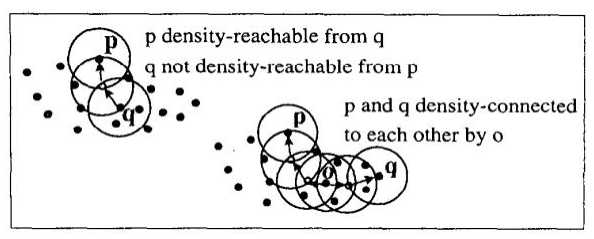
密度可达它不是一个对称的概念,从p到q是密度可达的不能推出从q到p是密度可达的,如果最后一个点不是核心点的话,显然是对称可达是不成立的。密度相连是中间有一个跳板o,通过o到p是密度可达的,然后从o到q也是密度可达的,那我们称p和q之间是密度相连的,密度相连它是一个对称的概念,从p到q是密度相连的话,那么从q到p他也是密度相连的。
算法的流程:
原文:https://www.cnblogs.com/wisir/p/12113379.html