
如果训练集大小??是 500 万或 5000 万或者更大的 一个数,在对整个训练集执行梯度下降法时,必须处理整个训练集,然后才能进行一步梯度下降法。所以如果在处理完整个 500 万个样本的训练集之前,先让梯度下降法处理一部分, 算法速度会更快。
batch 梯度下降法指的是之前讲过的梯度下降法算法, 就是同时处理整个训练集。 相比之下,mini-batch 梯度下降法,指的是每次同时处理的单个的 mini-batch \(??^{\{??\}}\) 和 \(??^{\{??\}}\),而不是同时处理全部的??和??训练集。
mini-batch 梯度下降法的原理:

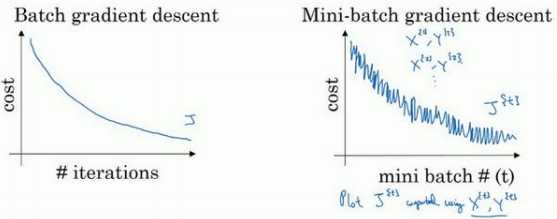
在训练中需要决定的变量之一是 mini-batch 的大小,??就是训练集的大小,极端情况下:
1、如果 mini-batch 的大小等于??,其实就是 batch 梯度下降法。
2、假设 mini-batch 大小为 1,就有了新的算法,叫做随机梯度下降法, 每个样本都是独立的 mini-batch。
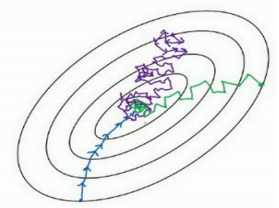
实际上选择的 mini-batch 大小在二者之间,大小在 1 和??之间,而 1 太小了,??太大 了,原因在于如果使用 batch 梯度下降法,mini-batch 的大小为??,每个迭代需要处理大量训练样本,该算法的主要弊端在于特别是在训练样本数量巨大的时候,单次迭代耗时太长。如果使用随机梯度下降法,如果只要处理一个样本,没有问题,通过减小学习率,噪声会被改善或有所减小,但随机梯度下降法的一大缺点是, 会失去所有向量化带给的加速,因为一次性只处理了一个训练样本,这样效率过于低下。
之后需要使用到一些优化算法,它们比梯度下降法快,但要理解这些算法,需要用到指数加权平均,在统计中也叫做指数加权移动平均:
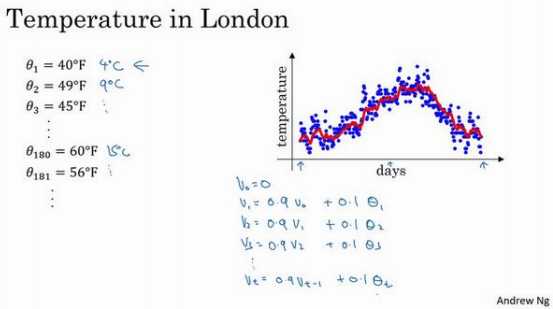
要做的是,
首先使\(??_0 = 0\),每天,需要使用 0.9 的加权数之前的数值加上当日温度的 0.1 倍,即\(??_1 = 0.9??_0 + 0.1??_1\),所以这里是第一天的温度值。
第二天,又可以获得一个加权平均数,0.9 乘以之前的值加上当日的温度 0.1 倍,即\(??_2 = 0.9??_1 + 0.1??_2\),以此类推。 第二天值加上第三日数据的 0.1,如此往下。
把 0.9 这个常数变成??,将之 前的 0.1 变成(1 ? ??),即\(??_?? = ????_{???1} + (1 ? ??)??_t\)。
在计算时可视\(??_??\)大概是 \(\frac{1}{ (1???)}\)的每日温度,将??设置为接近 1 的一个值,比如 0.98,计算 1 / (1?0.98) = 50,这就是粗 略平均了一下,过去 50 天的温度,这时作图可以得到绿线。
原因在于多平均了几天的温度, 所以这个曲线,波动更小,更加平坦,缺点是曲线进一步右移,因为现在平均的温度值更多, 要平均更多的值,指数加权平均公式在温度变化时,适应地更缓慢一些,所以会出现一定延迟,因为当?? = 0.98,相当于给前一天的值加了太多权重,只有 0.02 的权重给了当日的值, 所以温度变化时,温度上下起伏,当?? 较大时,指数加权平均值适应地更缓慢一些。
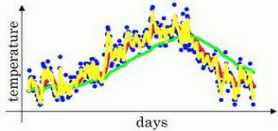
如果??是另一个极端值,比如说 0.5,作图运行后得到黄线。由于仅平均了两天的温度,平均的数据太少,所以得到的曲线有更多的噪声,有可能出现异常值,但是这个曲线能够更快适应温度变化。
进一步地分析,来理解如何计算出每日温度的平均值。
理解??100是什么?
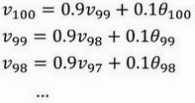
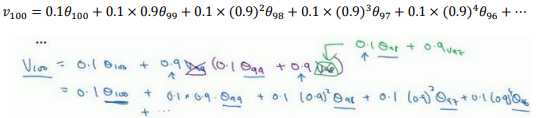
这是一个加和并平均,
所有的这些系数\((,,,)(0.1,0.1 × 0.9,0.1 × (0.9)^2,0.1 × (0.9)^3 …)\),相加起来为 1 或者逼近 1,我们称之为偏差修正。
需要平均多少天的温度的计算思路:
\((0.9)^{10}≈0.35\),这个值大概是1/e,也就是说:
ε=0.1,\((1?ε)^{\frac{1}{(1?ε)}} ≈\frac{1}{e}\)大约是 0.34, 0.35,换句话说, 10 天后,曲线的高度下降到\(\frac{1}{\epsilon}\)相当于在峰值的\(\frac{1}{e}\)。
所以当β=0.9,也即ε=1?β时只关注了过去 10天的温度,因为 10 天后,权重下降到不到当日权重的三分之一。
所以估算大约平均多少天的温度时,我们使用公式:\(\frac{1}{1-\beta}\)
不过这只是思考的大致方向,并不是正式的数学证明。
指数加权平均数公式的好处之一在于,它占用极少内存,电脑内存中只占用一行数字而已,然后把最新数据代入公式,不断覆盖就可以了。如果要计算移动窗,直接算出过去 10 天的总和, 过去50 天的总和,除以 10 和 50 就好,如此往往会得到更好的估测。但缺点是,如果保存所有最近的温度数据,和过去 10 天的总和,必须占用更多的内存,执行更加复杂,计算成本也更加高昂。
偏差修正,可以让平均数运算更加准确
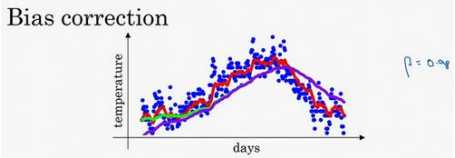
如果在??等于 0.98 的时候,得到的并不是绿色曲线,而是紫色曲线, 可以注意到紫色曲线的起点较低,来看看怎么处理。
计算移动平均数的时候,初始化\(,??_0 = 0,??_1 = 0.98??_0 + 0.02??_1\),如果一天温度是 40 华氏度,那么\(??_1 = 0.02??_1 = 0.02 × 40 = 8\),因此得到的值会小很多,所以第一天温度的估测不准。 \(??_2 = 0.98??_1 + 0.02??_2\),如果代入\(??_1\),然后相乘,所以 \(??_2 = 0.98 × 0.02??_1 + 0.02??_2 = 0.0196??_1 + 0.02??_2\),假设\(??_1\)和\(??_2\)都是正数,计算后\(??_2\)要远小于??1和??2,所以??2不能很好估测 出这一年前两天的温度。
有个办法可以修改这一估测,让估测变得更好,更准确,特别是在估测初期,也就是不用\(??_??\),而是用$ \frac{??_??}{ 1???^??}$,t 就是现在的天数。
举个具体例子,当?? = 2时,\(1 ? ??^?? = 1 ? 0.982 = 0.0396\), 因此对第二天温度的估测变成了$ \frac{??_2}{ 0.0396} = \frac{0.0196??_1+0.02??_2}{ 0.0396} \(,也就是??1和??2的加权平均数,并去除了偏差。随着??增加,\)??^??$接近于 0,所以当??很大的时候,偏差修正几乎没有作用, 因此当??较大的时候,紫线基本和绿线重合了。
一种算法叫做 Momentum,或者叫做动量梯度下降法,运行速度几乎总是快于标准的梯度下降算法,简而言之,基本的想法就是计算梯度的指数加权平均数,并利用该梯度更新权重:
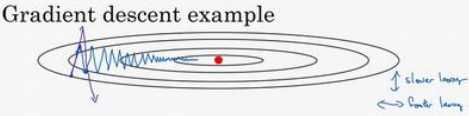
如果要用较大的学习率(紫色箭头),结果可能会偏离函数的范围,为了避免摆动过大,要用一个较小的学习率。
另一个看待问题的角度是,在纵轴上,希望学习慢一点,因为不想要这些摆动,但是在横轴上,希望加快学习,希望快速从左向右移,移向最小值,移向红点。所以使用动量梯度下降法。
需要做的是,在每次迭代中,确切来说在第??次迭代的过程中,计算微分????,??b:
计算\(??_{????} = ????_{????} +(1 ? ??)??_??\),这跟我们之前的计算相似,也就是\(?? = ???? + (1 ? ??)??_??\),????的移动平均数,接 着同样地计算\(,??_{????},??_{????} = ????_{????} + (1 ? ??)????\),然后重新赋值权重,\(??: = ?? ? ????_{????}\),同样\(??: = ?? ? ????_{????}\),这样就可以减缓梯度下降的幅度。
在上几个导数中,会发现这些纵轴上的摆动平均值接近于零,所以在纵轴方向,平均过程中,正负数相互抵消,所以平均值接近于零。但在横轴方向,所有的微分都指向横轴方向,因此横轴方向的平均值仍然较大,因此用算法几次迭代后,动量梯度下降法,最终纵轴方向的摆动变小了,横轴方向运动更快,算法走了一 条更加直接的路径,在抵达最小值的路上减少了摆动。
RMSprop 的算法, 全称是 root mean square prop 算法,它也可以加速梯度下降:
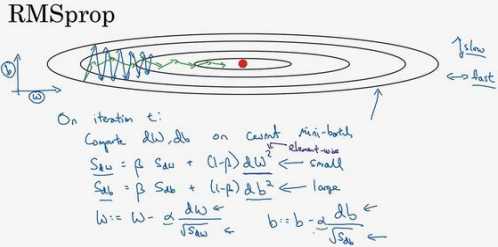
在第??次迭代中,该算法会照常计算当下 mini-batch 的微分????,????,保留这个指数加权平均数,并用到新符号\(??_{????}\),而不是\(??_{????}\),因此\(??_{????} = ????_{????} + (1 ? ??)????^2\),这个平方的操作是针对这一整个符号的,这样做能够保留微分平方的加权平均数,同样\(??_{????} = ????_{????} + (1 ? ??)????^2\)。
接着 RMSprop 更新参数值,\(,??: = ?? ? ?? \frac{????}{\sqrt{??_{????} }},??: = ?? ? ?? \frac{????}{\sqrt{??_{????}}}\) ,其原理:
希望减缓纵轴上的摆动,所以有了\(??_{????}\)和\(??_{????}\),希望\(??_{????}\)会相对较小,所以要除以一个较小的数,而希望\(??_{????}\)又较大,所以这里要除以较大的数字,这样就可以减缓纵轴上的变化。
这些微分,垂直方向的要比水平方向的大得多,所以斜率在??方向特别大,所以这些微分中,????较大,????较小,因为函数的倾斜程度,在纵轴 上,也就是 b 方向上要大于在横轴上,也就是??方向上。????的平方较大,所以\(??_{????}\)也会较大, 而相比之下,????会小一些,亦或????平方会小一些,因此\(??_{????}\)会小一些,结果就是纵轴上的 更新要被一个较大的数相除,就能消除摆动,而水平方向的更新则被较小的数相除。
RMSprop 的影响就是更新最后会变成绿色线,纵轴方向上摆动较小,而横轴方向继续推进。还有个影响就是,可以用一个更大学习率??,然后加快学习,而无须在纵轴上垂直方向偏离。RMSprop,全称是均方根,因为将微分进行平方,然后最后使用平方根。
Adam 优化算法基本上就是将 Momentum 和 RMSprop 结合在一起:

Adam 算法结合了 Momentum 和 RMSprop 梯度下降法,并且是一种极其常用的学 习算法,被证明能有效适用于不同神经网络,适用于广泛的结构。
本算法中有很多超参数,超参数学习率??很重要,也经常需要调试,可以尝试一系列值,然后看哪个有效。\(??_1\)常用的缺省值为 0.9,这是 dW 的移动平均数,也就是????的加权平 均数,这是 Momentum 涉及的项。至于超参数\(??_2\),Adam 论文作者,也就是 Adam 算法的发明者,推荐使用 0.999,这是在计算\((????)^2\)以及\((????)^2\)的移动加权平均值,关于??的选择其实没那么重要,Adam 论文的作者建议??为\(10^{?8}\),但并不需要设置它,因为它并不会影响算法表现。
Adam 代表的是 Adaptive Moment Estimation,\(??_1\)用于计算这个微分(????),叫做第一矩,\(??_2\)用来计算平方数的指数加权平均数\(()((????) ^2)\),叫做第二矩。

慢慢减少??的本质在于,在学习初期,能承受较大的步伐,但当开始收敛的时候, 小一些的学习率能让步伐小一些。
可以将??学习率设为\(?? =\frac{ 1}{ 1+???????????????????epoch?num }??_0\) ( decay-rate称为衰减率,epochnum 为代数,\(??_0\)为初始学习率)

比如,指数衰减,其中??相当于一个小于 1 的值,如\(?? = 0.95^{epoch?num}??_0\),所 以你的学习率呈指数下降。
人们用到的其它公式有\(?? = \frac{??}{epoch?num} ??_0\)或者\(?? = \frac{??}{\sqrt{??}}??_0\)(??为 mini-batch 的数字)。 有时也会用一个离散下降的学习率,也就是某个步骤有某个学习率,一会之后,学习率减少了一半,一会儿减少一半,一会儿又一半,这就是离散下降(discrete stair cease) 。
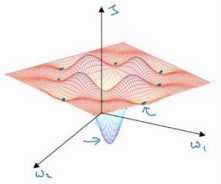
局部最优这里无过多理解。
原文:https://www.cnblogs.com/phoenixash/p/12117250.html