数学中有各式各样富含诗意的曲线,螺旋线就是其中比较特别的一类。螺旋线这个名词来源于希腊文,它的原意是“旋卷”或“缠卷”。例如,平面螺旋线便是以一个固定点开始向外逐圈旋绕而形成的曲线。
阿基米德螺线和黄金螺旋线就是典型的螺旋线。下面我们探讨一种典型的螺旋线:圆内螺线。
在固定的大圆中内切一个运动的小圆,在小圆滚动的过程中,其上一个定点P所形成的轨迹,即为圆内螺线。点P会随着两圆半径比值的不同而出现不同轨迹。例如,当小圆半径等于大圆的四分之一时,形成的轨迹则是星形线,如图1所示。参见百度百科的词条“圆内螺线”(https://baike.so.com/doc/388206-411038.html)。
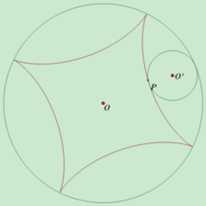
图1 圆内螺线的形成示意图
圆内螺线的笛卡尔坐标参数方程为:
x=cosθ+[cos(nθ)]/n
y=sinθ-[sin(nθ)]/n (0≤θ≤2π, n为大圆半径与小圆半径的比值)
编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>圆内螺线(一)</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext(‘2d‘);
context.fillStyle="#EEEEFF";
context.fillRect(0,0,300,300);
context.strokeStyle="red";
context.lineWidth=2;
context.save();
context.translate(150,150);
var R=80; // R+r 为大圆半径
var r=20; // 小圆半径
context.beginPath();
context.arc(0,0,R+r,0,Math.PI*2,true);
context.closePath();
context.stroke();
context.beginPath();
context.arc(0,0,R-r,0,Math.PI*2,true);
context.closePath();
context.stroke();
context.beginPath();
for (theta=0;theta<2*Math.PI;theta+=Math.PI/100)
{
n=R/r;
var x = R*(Math.cos(theta)+Math.cos(n*theta)/n);
var y = R*(Math.sin(theta)-Math.sin(n*theta)/n);
if (theta==0)
context.moveTo(x,y);
else
context.lineTo(x,y);
}
context.closePath();
context.stroke();
context.restore();
}
</script>
</head>
<body onload="draw(‘myCanvas‘);">
<canvas id="myCanvas" width="300" height="300"></canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中,再在浏览器中打开包含这段HTML代码的html文件,可以看到在画布中绘制出圆内螺线图案1,如图2所示。
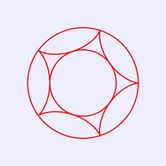
图2 圆内螺线图案1(R=5r)
将大圆半径与小圆半径的比值修改为9,即修改语句“var r=20;”为“var r=10”,则在画布中绘制出如图3所示的圆内螺线图案2。
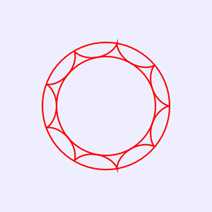
图3 圆内螺线图案2(R=9r)
我们修改圆内螺线的参数方程,使得螺线在交接处出现结环。修改的参数方程为:
n=(R+r)/r;
x = (R+r)*cos(θ)+(r+o)*cos(n*θ)
y = (R+r)*sin(θ)-(r+o)* sin (n*θ) (0≤θ≤2π)
编写的HTML文件内容如下。
<!DOCTYPE html>
<head>
<title>圆内螺线(二)</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext(‘2d‘);
context.fillStyle="#EEEEFF";
context.fillRect(0,0,300,300);
context.strokeStyle="red";
context.lineWidth=2;
context.save();
context.translate(150,150);
var R=60; // R+r 为大圆半径
var r=15; // 小圆半径
var o=15;
context.beginPath();
context.arc(0,0,R+2*r+o,0,Math.PI*2,true);
context.closePath();
context.stroke();
context.beginPath();
context.arc(0,0,R-o,0,Math.PI*2,true);
context.closePath();
context.stroke();
context.beginPath();
for (theta=0;theta<2*Math.PI;theta+=Math.PI/100)
{
n=(R+r)/r;
var x = (R+r)*Math.cos(theta)+(r+o)*Math.cos(n*theta);
var y = (R+r)*Math.sin(theta)-(r+o)*Math.sin(n*theta);
if (theta==0)
context.moveTo(x,y);
else
context.lineTo(x,y);
}
context.stroke();
context.restore();
}
</script>
</head>
<body onload="draw(‘myCanvas‘);">
<canvas id="myCanvas" width="300" height="300"></canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中,再在浏览器中打开包含这段HTML代码的html文件,可以看到在画布中绘制出带结环的圆内螺线图案,如图4所示。
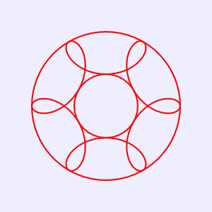
图4 带结环的圆内螺线图案
上面绘制图4的代码不是很完善,例如,我们修改语句“var r=15;”为“var r=24;”,其他语句保持不变,则在画布中绘制出如图5所示图案。这个图案显然不是一条封闭曲线,也就是图案未绘制完整。修改循环控制语句,使得θ范围为[0,3π],则在画布中绘制出如图6所示图案,这条曲线仍未封闭;当修改循环控制语句,使得θ范围为[0,4π],才在画布中绘制出如图7所示的封闭曲线图案。
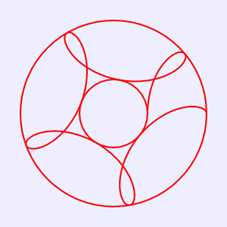
图5 0≤θ≤2π绘制的图案
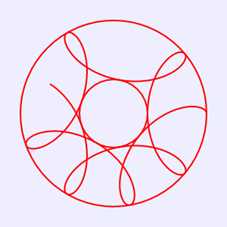
图6 0≤θ≤3π绘制的图案
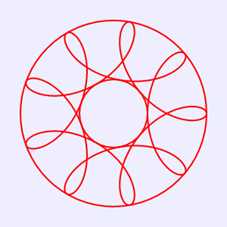
图7 0≤θ≤4π绘制的图案
如何修改程序,使得图案绘制时,无需事先确定θ的取值范围,当曲线闭合时,自动结束绘制呢?
取θ=0时的坐标(x0,y0)为起始点,之后按给定的参数方程依次计算坐标(x,y)并绘图,当计算的坐标点(x,y)与(x0,y0)重合时,结束图形绘制。
<!DOCTYPE html>
<head>
<title>圆内螺线(三)</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext(‘2d‘);
context.fillStyle="#EEEEFF";
context.fillRect(0,0,300,300);
context.strokeStyle="red";
context.lineWidth=2;
context.save();
context.translate(150,150);
var R=60; // R+r 为大圆半径
var r=24; // 小圆半径
var o=15;
context.beginPath();
context.arc(0,0,R+2*r+o,0,Math.PI*2,true);
context.closePath();
context.stroke();
context.beginPath();
context.arc(0,0,R-o,0,Math.PI*2,true);
context.closePath();
context.stroke();
var x1 = R+2*r+o; // theta=0 时的值
var y1 = 0;
var i = 1;
context.beginPath();
context.moveTo(x1,y1);
do {
if (i>20000) break; // θ最大可达200π
theta=i*Math.PI/100;
n=(R+r)/r;
var x2 = (R+r)*Math.cos(theta)+(r+o)*Math.cos(n*theta);
var y2 = (R+r)*Math.sin(theta)-(r+o)*Math.sin(n*theta);
context.lineTo(x2,y2);
i++;
} while (x2 != x1 && y2 != y1);
context.stroke();
context.restore();
}
</script>
</head>
<body onload="draw(‘myCanvas‘);">
<canvas id="myCanvas" width="300" height="300"></canvas>
</body>
</html>
修改参数方程为:
n=(R+r)/r;
x = (R+r)*cos(θ)-(r+o)*cos(n*θ)
y = (R+r)*sin(θ)-(r+o)* sin (n*θ) (0≤θ≤kπ,R、r、o取适当值)
编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>圆内螺线(四)</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext(‘2d‘);
context.fillStyle="#EEEEFF";
context.fillRect(0,0,300,300);
context.strokeStyle="red";
context.lineWidth=2;
context.save();
context.translate(150,150);
var R=180;
var r=-96;
var o=60;
var x0 = R-o; // theta=0 时的值
var y0 = 0;
var i = 1;
context.beginPath();
context.moveTo(x0,y0);
do {
if (i>20000) break; // θ最大可达200π
theta=i*Math.PI/100;
n=(R+r)/r;
var x = (R+r)*Math.cos(theta)-(r+o)*Math.cos(n*theta);
var y = (R+r)*Math.sin(theta)-(r+o)*Math.sin(n*theta);
context.lineTo(x,y);
i++;
} while (x != x0 && y != y0);
context.stroke();
context.restore();
}
</script>
</head>
<body onload="draw(‘myCanvas‘);">
<canvas id="myCanvas" width="300" height="300"></canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中,再在浏览器中打开包含这段HTML代码的html文件,可以看到在画布中绘制出另类螺旋线图案,如图8所示。

图8 R=180,r=-96,o=60时的螺旋线
修改绘制图8程序中的R、r、o初始值,可以绘制出不同的螺旋曲线。例如,若指定R=160,r=-96,o=40,则在画布中绘制出图9所示的图案;若指定R=160,r=-56,o=40,则在画布中绘制出图10所示的图案;若指定R=66,r=18,o=15,则在画布中绘制出图11所示的图案。

图9 R=160,r=-96,o=40时的螺旋线

图10 R=160,r=-56,o=40时的螺旋线
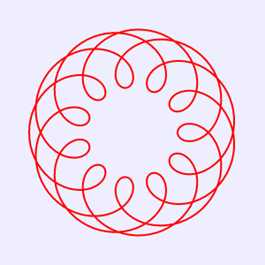
图11 R=66,r=18,o=15时的螺旋线
原文:https://www.cnblogs.com/cs-whut/p/12123746.html