主要讨论二元分类。
线性回归处理分类问题显然不靠谱,所以采用逻辑回归。
假设函数变为\(h_\theta(x)=g(\theta^TX)\),使得分类器的输出在[0,1]之间。
\(g(z)=\frac{1}{1+e^{-z}}\),叫做sigmoid函数:
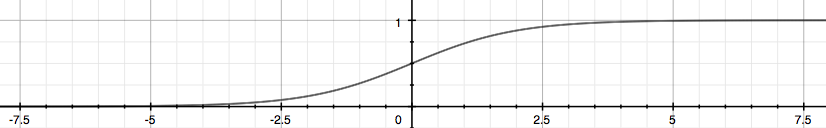
这个算出的值代表\(y\)是正向类的概率。
将阈值设为0.5,那么可以得知:当\(\theta^TX>=0\)时,预测\(y\)为1,否则为0。
Decision Boundary就是分隔\(y=1\)与\(y=0\)的边界,这个边界可以是任何形状,取决于假设函数。
上图:

效果非常好,那么如果训练集的数据不是这么规则呢?

将逻辑回归的代价函数定义为:
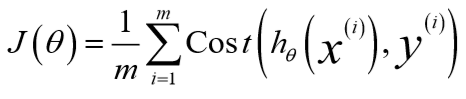
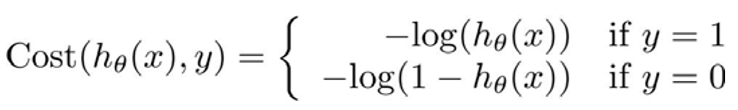
如果沿用线性回归的cost function,那么得到的\(J(\theta)\)是非凸的,这样不利于寻找全局最优解。
如果预测值\(h_\theta(x)=1\),实际的标签\(y\)也是1,那么\(cost=0\);
如果预测值\(h_\theta(x)=0\),而实际的标签\(y\)是1,那么\(cost=+\infin\),可以看作是对算法预测错误的惩罚。。。
同样的,\(y=0\)也具有相似的特征。
简化上述代价函数:
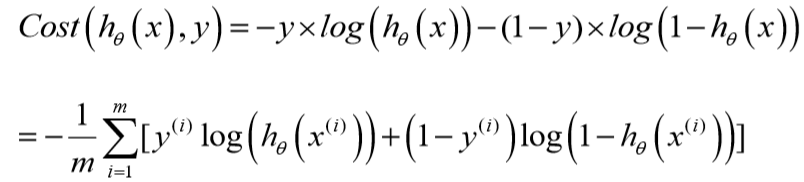
所以cost function的向量化表示:
\[h = g(X\theta) \]
\[J(\theta) = \frac{1}{m} \cdot \left(-y^{T}\log(h)-(1-y)^{T}\log(1-h)\right)\]
可以通过求出\(J(\theta)\)的最小值,得出参数\(\theta\),接着用\(h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}\)得到我们的预测值。
怎么求出\(J(\theta)\)的最小值呢?对了,就是Gradient Descent.

向量化表示:
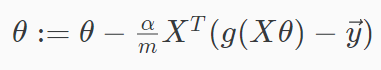
这个和之前线性回归更新参数的公式是一样的,但是由于\(h_\theta(x)\)不同,所以这两个梯度下降是完全不同的。
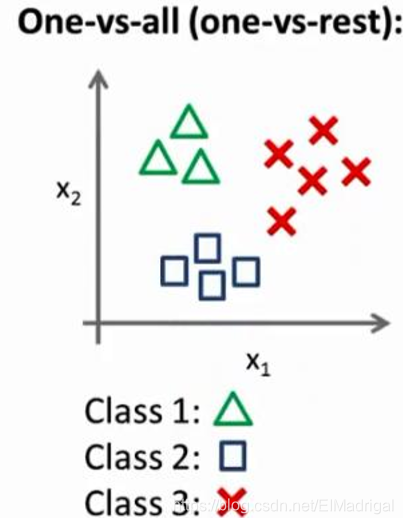
将其中的一个类作为正向类(y=1),其余作为负向类,分别训练出很多分类器,最后选择令输出值\(h_\theta^{i}(x)\)最大的一个\(i\)作为预测值。
相当于每一个分类器都可以识别一种类别:

原文:https://www.cnblogs.com/EIMadrigal/p/12130859.html