numpy :: 计算特征之间的余弦距离

 余弦距离在计算相似度的应用中经常使用，比如：

• 文本相似度检索
• 人脸识别检索
• 相似图片检索

原理简述

下面是余弦相似度的计算公式（图来自wikipedia）：

但是，余弦相似度和常用的L1距离或欧式距离的有所区别。

• 余弦相似度的取值范围在-1到1之间。完全相同时数值为1，相反反向时为-1，正交或不相关是为0。（如下图，来源）
• 欧式距离一般为正值，归一化之后在0~1之间。距离越小，越相似。

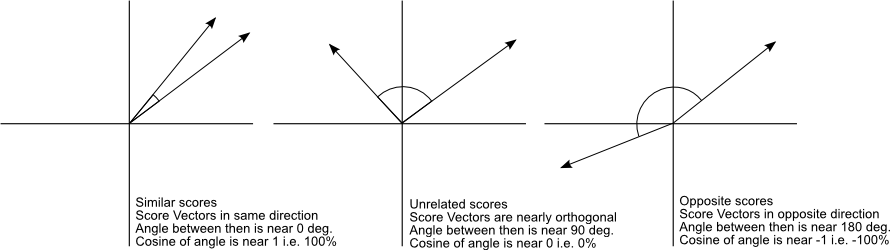
欧式距离用于相似度检索更符合直觉。因此在使用时，需要将余弦相似度转化成类似于欧氏距离的余弦距离。

维基页面中给出的角距离计算公式如下（图来自wikipedia）:

由于在计算图片或者文本相似度时，提取的特征没有负值，余弦相似度的取值为0~1，因此采用更简便的方法，直接定义为：

余弦距离 = 1- 余弦相似度

代码分析

代码如下，根据输入数据的不同分为两种模式处理。

• 输入数据为一维向量，计算单张图片或文本之间的相似度 （单张模式）
• 输入数据为二维向量（矩阵），计算多张图片或文本之间的相似度 （批量模式）

 1 import numpy as np
 2 def cosine_distance(a, b):
 3     if a.shape != b.shape:
 4         raise RuntimeError("array {} shape not match {}".format(a.shape, b.shape))
 5     if a.ndim==1:
 6         a_norm = np.linalg.norm(a)
 7         b_norm = np.linalg.norm(b)
 8     elif a.ndim==2:
 9         a_norm = np.linalg.norm(a, axis=1, keepdims=True)
10         b_norm = np.linalg.norm(b, axis=1, keepdims=True)
11     else:
12         raise RuntimeError("array dimensions {} not right".format(a.ndim))
13     similiarity = np.dot(a, b.T)/(a_norm * b_norm) 
14     dist = 1. - similiarity
15     return dist

6~7 行 ， np.linalg.norm 操作是求向量的范式，默认是L2范式，等同于求向量的欧式距离。

9~10行 ，设置参数 axis=1 。对于归一化二维向量时，将数据按行向量处理，相当于单独对每张图片特征进行归一化处理。

13行，np.dot 操作可以支持两种模式的运算，来自官方文档的解释：

• 一维向量求内积
• 二维向量（矩阵）求矩阵乘法 

 numpy.dot(a, b, out=None)

　　Dot product of two arrays. Specifically,

• If both a and b are 1-D arrays, it is inner product of vectors (without complex conjugation).

• If both a and b are 2-D arrays, it is matrix multiplication, but using matmul or a @ b is preferred.

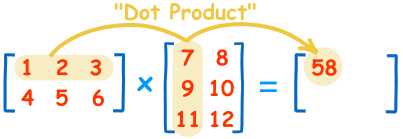
为了保持一致性，都使用了转置操作。如下图（来自博客），矩阵乘法按线性代数定义，必须是 行 × 列才能完成乘法运算。举例 32张128维特征进行运算，则应该是 32x128 * 128x32 才行。

参考文章

• 机器学习中的余弦相似度
• 理解矩阵乘法
• numpy.linalg.norm（求范数）

numpy :: 计算特征之间的余弦距离

原文：https://www.cnblogs.com/hansoluo/p/12123518.html