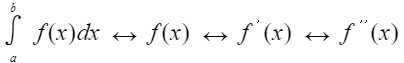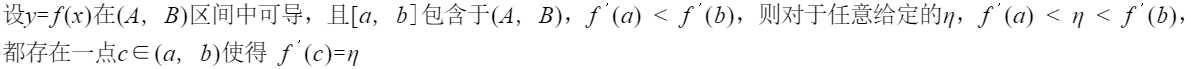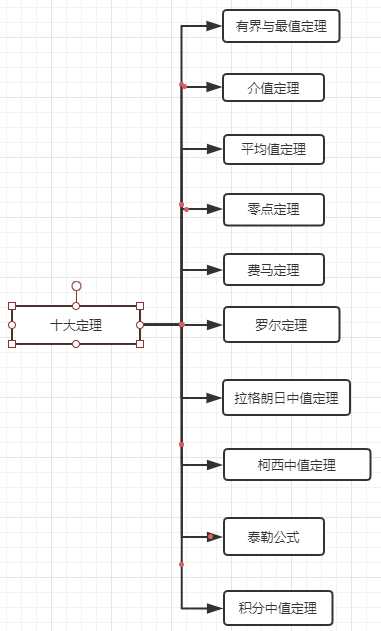

费马引理
- 设f(x)满足在x0点处 可导且取极值,则 f‘(x0)=0
- 点x0取极值则x0的导数必为0
费马引理的证明

证明区间内一点导数为零,考虑罗尔定理和费马引理
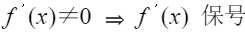
- 导数不为0,导函数必然保号(恒正或恒负,因为零点定理)
罗尔定理
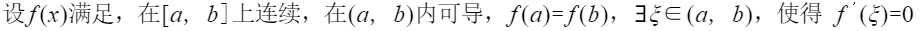
罗尔定理推广
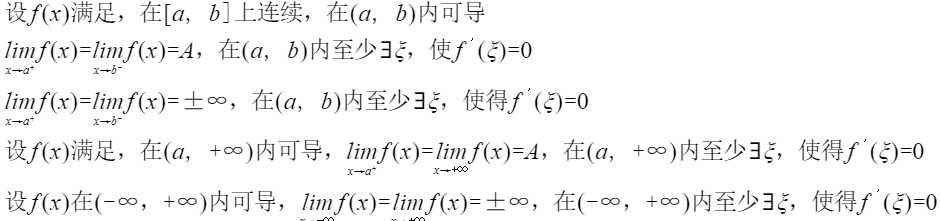
罗尔定理的使用
利用乘积求导公式的逆用,(uv)‘ = u‘v + uv‘
解题关键
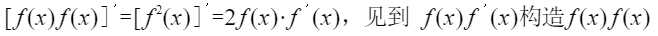
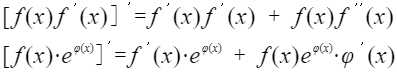
拉格朗日中值定理

柯西中值定理
- 设f(x),g(x)满足,在[a, b]连续,在(a, b)内可导,存在ξ ∈(a, b),g‘(x)≠0,使得
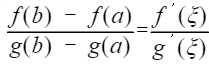
- 取g(x)=x,可以推出拉格朗日中值定理
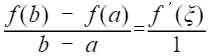 拉格朗日是柯西的特例
拉格朗日是柯西的特例
-
令f(a)=f(b),可以推出罗尔定理
泰勒公式

常用的级数

联系 f 与 f ‘ 考虑拉格朗日,联系 f 与 f ‘‘ 考虑泰勒公式
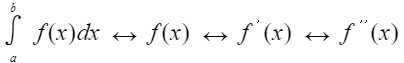
达布中值定理(导函数介质定理)
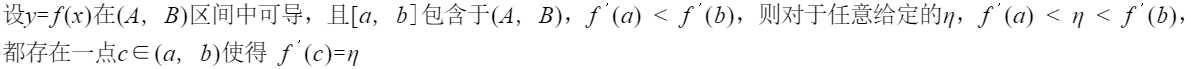
根据达布中值定理,如果导函数存在,要么连续,要么震荡
中值定理--函数的中值定理
原文:https://www.cnblogs.com/YC-L/p/12142755.html



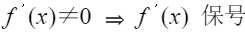
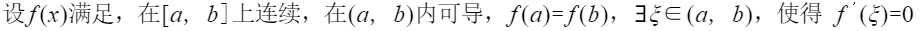
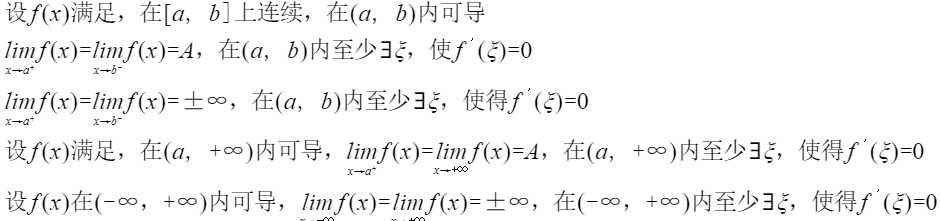
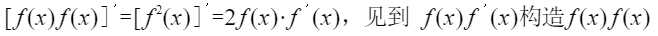
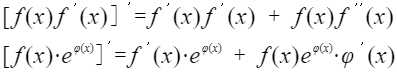

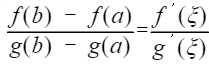
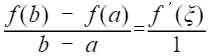 拉格朗日是柯西的特例
拉格朗日是柯西的特例