正态分布
qqnorm是一列分析,默认采用的是第一分位数以及第三分位数之间的数据来做正太分布的线
标准正态分布,查表值其实是标准差的值对应的到0点的面积,或者说是概率。标准差的计算是通过(X-μ)/ Δ,下图是标准正态分布图。
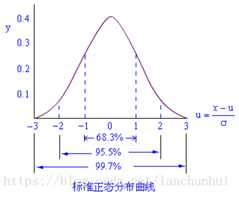
理解正态分布表很重要,正态分布表记录的是标准正态分布表,即:
X~N(0, 1)
描述的是均值为0,方差为1的正态分布,要理解正态分布表,首先理解正态分布图,如上图所示:横轴是标准正态分布的X,可以看到两边对称=>均值为0,所有的值的间隔为1=>方差是1;Y轴代表的是X的概率;
我们在查表的时候,其实是查的X到0点的区域的面积,在查表的时候,不是查的X,而是Z,这是为什么?因为我们现实处理的正态分布大部分都不是标准正态分布,而是正态分布,即X~N(μ,Δ),需要将分布转化为标准正态分布:
Z = (X-μ)/σ~N(0, 1)
通过转化公式将非标准的正态分布数据转化为标准正态分布的X,进而通过查表来查看F(X<x)的概率是多大(即X到0点的面积大小)。
其中-1和正1到0(均值)的距离被称之为一个标准差,-2和2到0的距离称之为2个标准差,2个标注差的面积总和95.5%也是统计学意义上面的大概率;在很多统计学中会认为如果数据之间的差距在2个标准差范围内是正常的,但是如果大于2个标准差,因为差距大于2个标准差范围是小于5%,属于小概率范围,如果差距是>2个标准差,就会认为可以推翻假设。比如在ACF中,如果残差大于2个标准差,就会认为数据已经发生了很大偏差,可以作为也异常值来处理。
R中和正态分布紧密相关的函数:
normdata = rnorm(100) # 生成随机的符合正态分布的数据
quantile(normdata) # 返回数据的分位数,默认四分位(0%,25%,75%,100%)
randu # 返回400个符合正态分布的随机数,
ppoints(x), qunif(x) #将会返回各个数据(索引值)的累计概率(这两个函数有区别吗),另外qunif是指QUnif,Q代表quantile分位数,Unif代表Uniform,均匀分布) runif(num, min=MIN, max=MAX),生成均匀分布数据
?
qqplot,qqnorm以及qqline
如何比较两个数据分布是否一致?或者想要知道某个数据序列是否来自于某个分布(比如正态分布)?
通过将两组数据,排序后,一组作为x,一组作为y,一一对应拼成坐标点<x, y>,在图中显示,如果两组数据分布相同应该能够看到一条直线,注意,这条直线重点关注一分位点和三分位点之间是否是直线(qqline就是做这件事情,所以qqplot一般会和qqline成对出现)。这个就是qqplot,当然qqplot还不只做了这个,如果x和y的数据数量不一致,将会通过内插法来进行填补,使之数量保持一致。
qqnorm则是更加直接,你只需要传入你想要判断是否是正态分布的数据集合即可,qqnorm将会根据你传入数据的数量生成一组同数量的符合标准正态分布的数据,作为x,你输入的数据作为y,然后进行展示。
data(trees) qqnorm(trees$Girth)
?
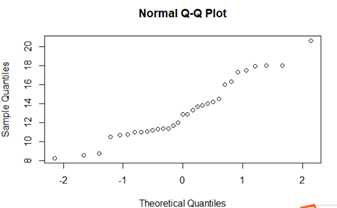
看到纵坐标写的是Theoretcal Quantiles,就是x是生成的值
qqline的那条线其实是输入数据集的四分位的一分位点(下四分位)和三分位(上四分位)为点连接起来,做一条线,用意就是说明如果是整体分布,那么数据趋势应该是一条直线。
qqline(trees$Girth)
?
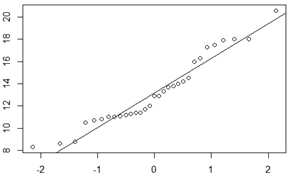
怎么定位上下四分卫呢?
quantile(trees$Girth)
0% 25% 50% 75% 100%
8.30 11.05 12.90 15.25 20.60
比较灵异的事情发生了,就是你会发现15.25根本没有点被贯穿,这一点非常奇怪,我试了trees$Height以及trees$Volumn都会有25%的点和75%的点被贯穿,但是就是Girth,75%被狗吃了的感觉。
不过不纠结了,qqline的就是这样一条线。
?
Shapiro-Wilk检验
上述描述都是基于图形来判断,还有根据数据来判断,这个就是Shapiro-Wilk检验,简称SW test。
原理是这样的:
H0: 样本数据与正态分布没有显著区别。
HA: 样本数据与正态分布存在显著区别。
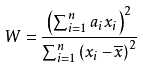
W是一个SW的一个统计量(假设考察的对象),在正态分布条件下,w值将会接近于1,并且是大概率如此 => p值要大于0.05,这样就会支持原假设。
shapiro.test(trees$Girth)
Shapiro-Wilk normality test
?
data: trees$Height
W = 0.96545, p-value = 0.4034
?
W值接近于1,p-value远大于0.05,所以是符合正态分布
shapiro.test(trees$Volume)
...(省略)
W = 0.88757, p-value = 0.003579
?
这个差的有点远了,真的是这样吗?我们看通过qqnorm以及qqline图来了解一下:
> qqnorm(trees$Volume) > qqline(trees$Volume)
?
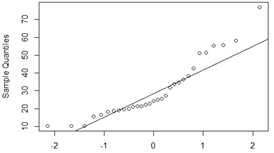
确实距离正态分布太远了,所以拒绝原假设,该数据不符合正态分布。
?
什么时候需要考察数据是否符合正态分布?
只有在需要线性根据调查的结果,有五类分析需要考虑并验证正态分布:
关于线性回归需要考察数据是否符合正态分布,因为线性回归牵涉到最小二乘法,使用最小二乘法的时候,需要对应变量是符合正态分布的。至于为什么呢?这个是因为线性回归的假设是:
Y = ωX + ε,其中ε是符合正态分布的噪声。根据概率中的定义,ε为正态分布,那么Y就一定是正态分布,即ε ~ N(μ, σ2)可以推知Y ~ N(ωX+ε, σ2)。
对于线性回归模型,当因变量服从正态分布,误差项满足高斯–马尔科夫条件(零均值、等方差、不相关)时,回归参数的最小二乘估计是一致最小方差无偏估计.
?
如何进行正态分布
取对数,开根号,这些机器学习里面常见的处理方式,其实都是统计学中CoxBox变换:
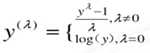
MASS库中有一个boxcox函数(显示b,后面c,符合字典顺序哦)可以求得
# 通过boxcox函数可以获得一系列的λ值(集合),seq参数里面前两个是λ尝试范围的起始 # 和终止;最后一个by参数代表步长,每次尝试都会增加步长个单位,再来进行计算,调用 # boxcox你将会得到一张图,这张图显示了那个点对应的极大似然值。 > bc = boxcox(lm.sol, lambda=seq(0, 1, by=0.1)) > max_index = which(bc$y==max(bc$y)) #获取所有的index值中对应的y值最大的 > lambda = bc$x[max_index] # 获取对应的lambda值,参考上面的公式 # 建立线性关系,参考上面公式,到此基于新的数据源的模型诞生了,这里注意,因为λ # 值是≠0的,所以取用的是上面的公式,如果是=0,则取用log处理方式。 > lm.bc = lm((y^lambda -1) ~x)
附录
?
内插法
直线内插法,使之根据两点做出一条直线,然后取这条直线两点之间的点作为插入数据。还有KNN内插法。
?
参考
https://www.jianshu.com/p/e202069489a6 【统计与检验-1】Shapiro-Wilk检验
https://blog.csdn.net/zzminer/article/details/8858469 Shapiro-Wilk (SW) 检验
https://blog.csdn.net/fitzgerald0/article/details/75212215 R中的Box-Cox变换
?
内插法
https://baike.baidu.com/item/%E5%86%85%E6%8F%92%E6%B3%95
http://www.sohu.com/a/16101010_126457
?
什么时候需要考察正态分布
https://cosx.org/2013/01/story-of-normal-distribution-1
https://blog.csdn.net/u010462995/article/details/70847146
https://blog.csdn.net/lilyth_lilyth/article/details/8975976
https://blog.csdn.net/m0_37228052/article/details/89639426 提出了五大操作需要考虑正态分布
原文:https://www.cnblogs.com/xiashiwendao/p/12150237.html