10.3图的表示和同构(Graph Representations and Isomorphism)

图的表示

邻接表表示法(Adjacency lists)

邻接矩阵表示法(Adjacency matrices)

关联矩阵表示法(Incidence matrices)

图的同构

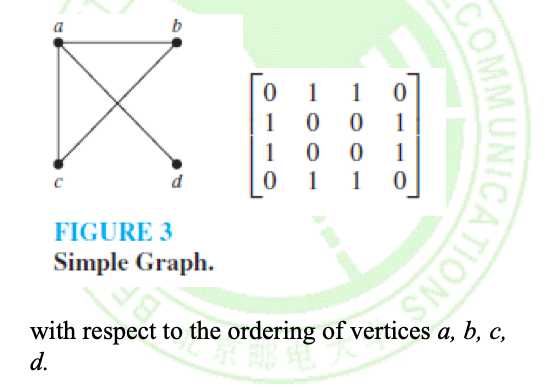
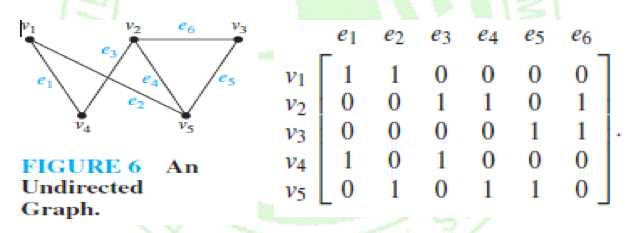
通俗定义:两个图形是同构的，当且仅当(iff)除了它们的节点名称之外，它们是相同的。
正式定义:G1=(V1, E1) 和G2=(V2, E2)之间存在顶点上的双射(bijection)函数f:V1 -> V2 ，使得任意a，b∈V1，有a和b在G1中相邻，那么f(a)和f(b)也在G2中相邻
图同构 ==》 子图必定也同构

10.3图的表示和同构(Graph Representations and Isomorphism)

原文：https://www.cnblogs.com/SpicyArticle/p/12151018.html