哈夫曼树,也称最优二叉树,它是n个带权叶子结点构成的所有二叉树中,带权路径长度最小的二叉树。
所谓树的带权路径长度,就是树中所有的叶节点的权值乘上其到根结点的路径长度。
权值越大的结点离根结点越近的二叉树才是最优二叉树。
树的带权路径路径长度(WPL)是从树根到每一结点的路径长度之和,记为WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。
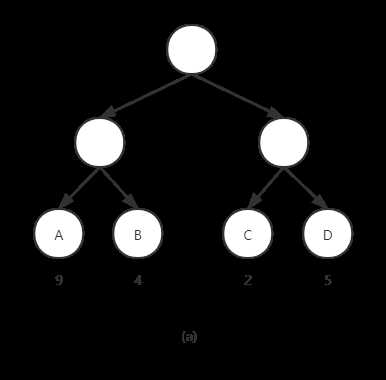
(a)WPL = 9*2 + 4*2 + 2*2 + 5*2 = 40
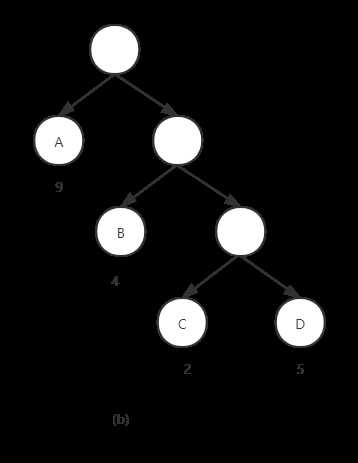
(b)WPL = 9 + 4*2 + 2*3 + 5*3 = 38
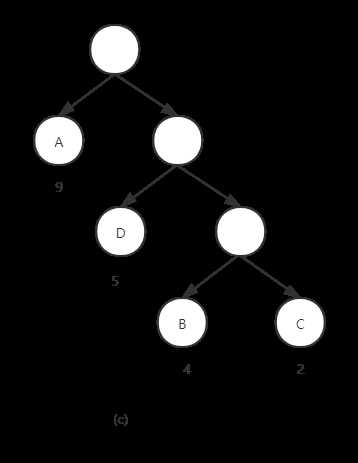
(c)WPL = 9 + 5*2 + 4*3 + 2*3 = 37
所以(c)是最优二叉树。
给出一组数字,对这组数字进行排序,排序方式如下:
(1)取出根节点权值最小的两颗二叉树
(2)组成一颗新的二叉树,前面取出来的两颗二叉树是新二叉树的两个子树
(3)新二叉树的根节点的权值是前两个二叉树的根节点的权值之和
如图:

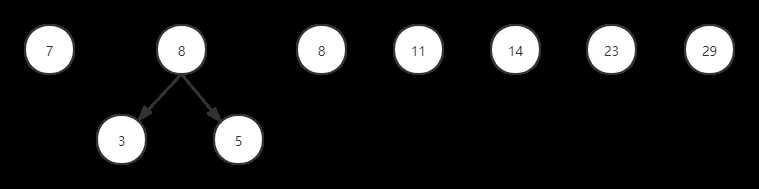
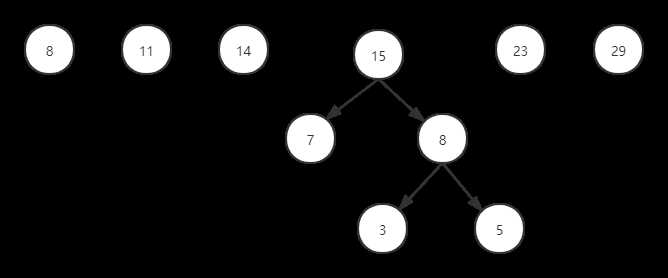
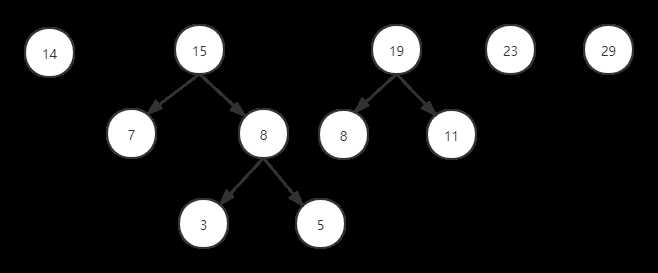
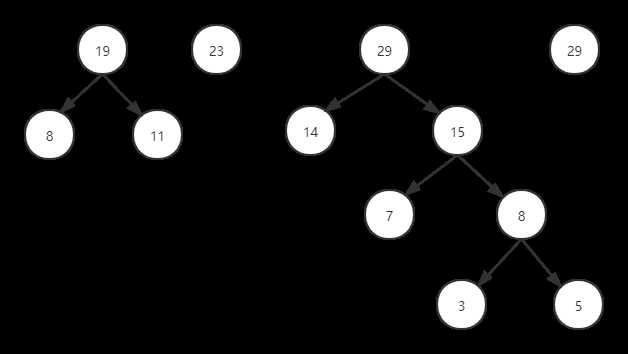
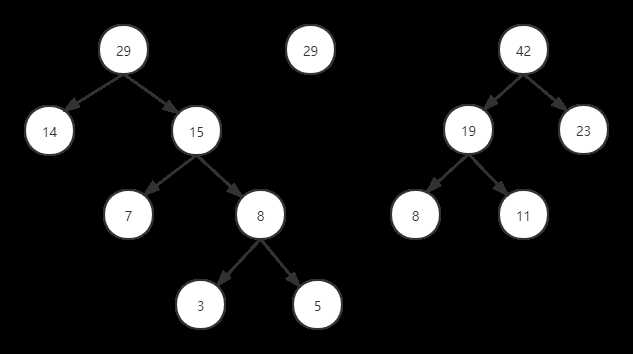
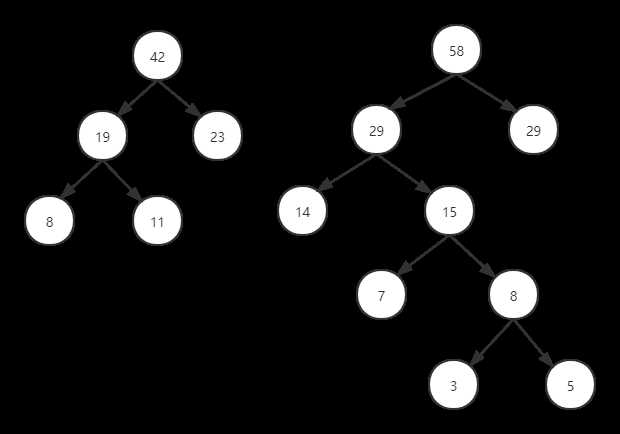

(1)定义哈夫曼树数据结构:
public class Node<E> { E data; double weight; Node leftChild; Node rightChild; public Node(E data, double weight) { super(); this.data = data; this.weight = weight; } public String toString() { return "Node[data=" + data + ", weight=" + weight + "]"; } }
(2)根据树的结点形成哈夫曼树:
/** * 构造哈夫曼树 * * @param nodes * 节点集合 * @return 构造出来的哈夫曼树的根节点 */ private static Node createTree(List<Node> nodes) { // 只要nodes数组中还有2个以上的节点 while (nodes.size() > 1) { quickSort(nodes); //获取权值最小的两个节点 Node left = nodes.get(nodes.size()-1); Node right = nodes.get(nodes.size()-2); //生成新节点,新节点的权值为两个子节点的权值之和 Node parent = new Node(null, left.weight + right.weight); //让新节点作为两个权值最小节点的父节点 parent.leftChild = left; parent.rightChild = right; //删除权值最小的两个节点 nodes.remove(nodes.size()-1); nodes.remove(nodes.size()-1); //将新节点加入到集合中 nodes.add(parent); } return nodes.get(0); } /** * 将指定集合中的i和j索引处的元素交换 * * @param nodes * @param i * @param j */ private static void swap(List<Node> nodes, int i, int j) { Node tmp; tmp = nodes.get(i); nodes.set(i, nodes.get(j)); nodes.set(j, tmp); } /** * 实现快速排序算法,用于对节点进行排序 * * @param nodes * @param start * @param end */ private static void subSort(List<Node> nodes, int start, int end) { if (start < end) { // 以第一个元素作为分界值 Node base = nodes.get(start); // i从左边搜索,搜索大于分界值的元素的索引 int i = start; // j从右边开始搜索,搜索小于分界值的元素的索引 int j = end + 1; while (true) { // 找到大于分界值的元素的索引,或者i已经到了end处 while (i < end && nodes.get(++i).weight >= base.weight) ; // 找到小于分界值的元素的索引,或者j已经到了start处 while (j > start && nodes.get(--j).weight <= base.weight) ; if (i < j) { swap(nodes, i, j); } else { break; } } swap(nodes, start, j); //递归左边子序列 subSort(nodes, start, j - 1); //递归右边子序列 subSort(nodes, j + 1, end); } } public static void quickSort(List<Node> nodes){ subSort(nodes, 0, nodes.size()-1); } //广度优先遍历 public static List<Node> breadthFirst(Node root){ Queue<Node> queue = new ArrayDeque<Node>(); List<Node> list = new ArrayList<Node>(); if(root!=null){ //将根元素加入“队列” queue.offer(root); } while(!queue.isEmpty()){ //将该队列的“队尾”元素加入到list中 list.add(queue.peek()); Node p = queue.poll(); //如果左子节点不为null,将它加入到队列 if(p.leftChild != null){ queue.offer(p.leftChild); } //如果右子节点不为null,将它加入到队列 if(p.rightChild != null){ queue.offer(p.rightChild); } } return list; }
(3)测试方法:
public static void main(String[] args) { List<Node> nodes = new ArrayList<Node>(); nodes.add(new Node("A", 40.0)); nodes.add(new Node("B", 8.0)); nodes.add(new Node("C", 10.0)); nodes.add(new Node("D", 30.0)); nodes.add(new Node("E", 10.0)); nodes.add(new Node("F", 2.0)); Node root = HuffmanTree.createTree(nodes); System.out.println(breadthFirst(root)); }
结果:
[Node[data=null, weight=100.0], Node[data=A, weight=40.0], Node[data=null, weight=60.0], Node[data=null, weight=30.0], Node[data=D, weight=30.0], Node[data=C, weight=10.0], Node[data=null, weight=20.0], Node[data=null, weight=10.0], Node[data=E, weight=10.0], Node[data=F, weight=2.0], Node[data=B, weight=8.0]]
原文:https://www.cnblogs.com/strong-FE/p/12152009.html