方法二:动态规划
最近我总结了“动态规划”问题的思考路径,供大家参考。
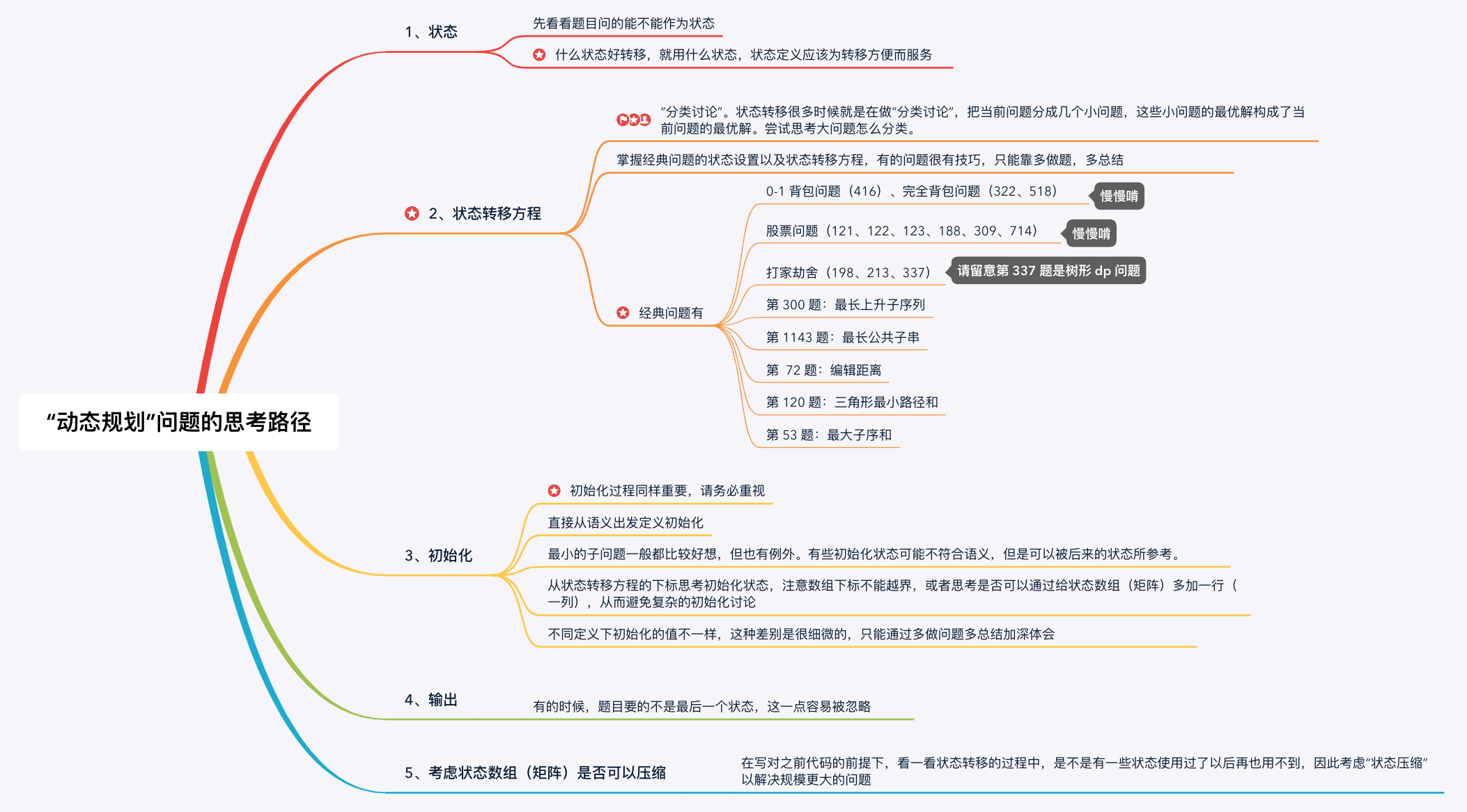
1、思考状态
状态先尝试“题目问什么,就把什么设置为状态”。然后考虑“状态如何转移”,如果“状态转移方程”不容易得到,尝试修改定义,目的仍然是为了方便得到“状态转移方程”。
2、思考状态转移方程(核心、难点)
状态转移方程是非常重要的,是动态规划的核心,也是难点,起到承上启下的作用。
技巧是分类讨论。对状态空间进行分类,思考最优子结构到底是什么。即大问题的最优解如何由小问题的最优解得到。
归纳“状态转移方程”是一个很灵活的事情,得具体问题具体分析,除了掌握经典的动态规划问题以外,还需要多做题。如果是针对面试,请自行把握难度,我个人觉得掌握常见问题的动态规划解法,明白动态规划的本质就是打表格,从一个小规模问题出发,逐步得到大问题的解,并记录过程。动态规划依然是“空间换时间”思想的体现。
3、思考初始化
初始化是非常重要的,一步错,步步错,初始化状态一定要设置对,才可能得到正确的结果。
角度 1:直接从状态的语义出发;
角度 2:如果状态的语义不好思考,就考虑“状态转移方程”的边界需要什么样初始化的条件;
角度 3:从“状态转移方程”方程的下标看是否需要多设置一行、一列表示“哨兵”,这样可以避免一些边界的讨论,使得代码变得比较短。
4、思考输出
有些时候是最后一个状态,有些时候可能会综合所有计算过的状态。
5、思考状态压缩
“状态压缩”会使得代码难于理解,初学的时候可以不一步到位。先把代码写正确,然后再思考状态压缩。
状态压缩在有一种情况下是很有必要的,那就是状态空间非常庞大的时候(处理海量数据),此时空间不够用,就必须状态压缩。
作者:liweiwei1419
链接:https://leetcode-cn.com/problems/longest-palindromic-substring/solution/zhong-xin-kuo-san-dong-tai-gui-hua-by-liweiwei1419/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
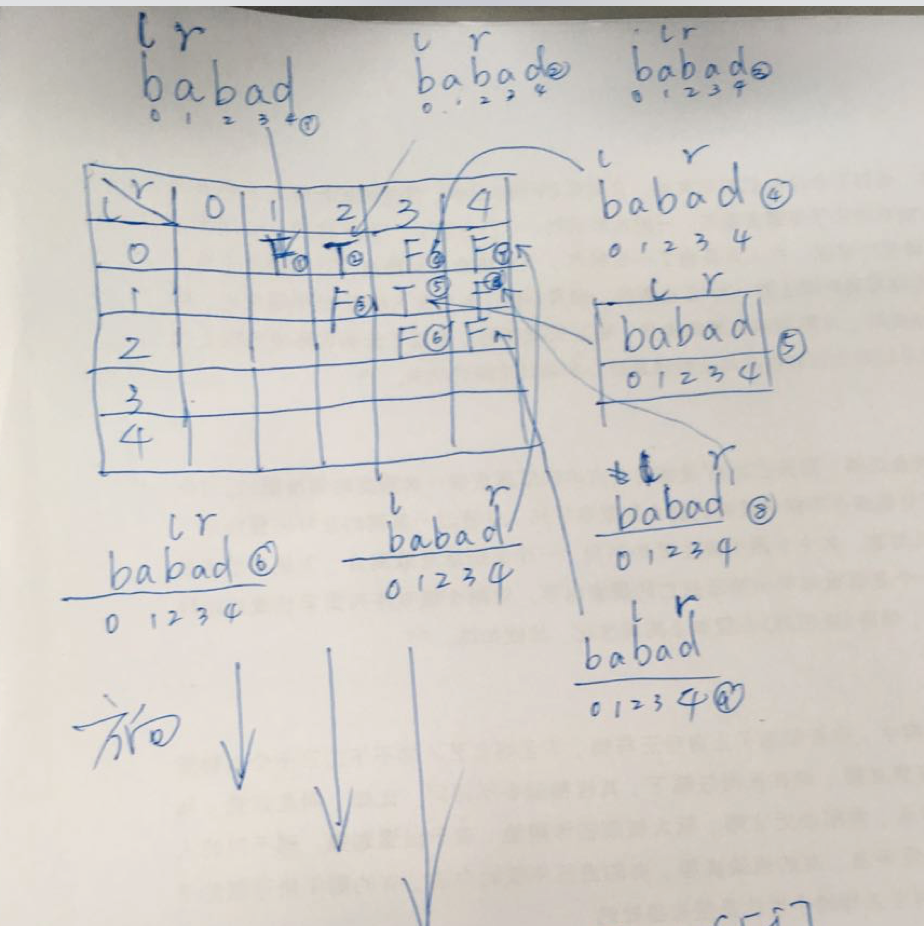
这道题比较烦人的是判断回文子串。因此需要一种能够快速判断原字符串的所有子串是否是回文子串的方法,于是想到了“动态规划”。
“动态规划”最关键的步骤是想清楚“状态如何转移”,事实上,“回文”是天然具有“状态转移”性质的。直觉上,如果一个回文去掉两头以后,剩下的部分依然是回文(这里暂不讨论边界)。
依然从回文串的定义入手:
1、如果一个字符串的头尾两个字符都不相等,那么这个字符串一定不是回文串;
2、如果一个字符串的头尾两个字符相等,才有必要继续判断下去。
(1)如果里面的子串是回文,整体就是回文串;
(2)如果里面的子串不是回文串,整体就不是回文串。
即在头尾字符相等的情况下,里面子串的回文性质据定了整个子串的回文性质,这就是状态转移。因此可以把“状态”定义为原字符串的一个子串是否为回文子串。
第 1 步:定义状态
dp[i][j] 表示子串 s[i, j] 是否为回文子串。
第 2 步:思考状态转移方程
这一步在做分类讨论(根据头尾字符是否相等),根据上面的分析得到:
dp[i][j] = (s[i] == s[j]) and dp[i + 1][j - 1]
分析这个状态转移方程:
(1)“动态规划”事实上是在填一张二维表格,i 和 j 的关系是 i <= j ,因此,只需要填这张表的上半部分;
(2)看到 dp[i + 1][j - 1] 就得考虑边界情况。
边界条件是:表达式 [i + 1, j - 1] 不构成区间,即长度严格小于 2,即 j - 1 - (i + 1) + 1 < 2 ,整理得 j - i < 3。(最里面的一个或者俩个数字)
这个结论很显然:当子串 s[i, j] 的长度等于 2 或者等于 3 的时候,我其实只需要判断一下头尾两个字符是否相等就可以直接下结论了。
如果子串 s[i + 1, j - 1] 只有 1 个字符,即去掉两头,剩下中间部分只有 11 个字符,当然是回文;
如果子串 s[i + 1, j - 1] 为空串,那么子串 s[i, j] 一定是回文子串。
因此,在 s[i] == s[j] 成立和 j - i < 3 的前提下,直接可以下结论,dp[i][j] = true,否则才执行状态转移。
(这一段看晕的朋友,直接看代码吧。我写晕了,车轱辘话来回说。)
第 3 步:考虑初始化
初始化的时候,单个字符一定是回文串,因此把对角线先初始化为 1,即 dp[i][i] = 1 。
事实上,初始化的部分都可以省去。因为只有一个字符的时候一定是回文,dp[i][i] 根本不会被其它状态值所参考。
第 4 步:考虑输出
只要一得到 dp[i][j] = true,就记录子串的长度和起始位置,没有必要截取,因为截取字符串也要消耗性能,记录此时的回文子串的“起始位置”和“回文长度”即可。
第 5 步:考虑状态是否可以压缩
因为在填表的过程中,只参考了左下方的数值。事实上可以压缩,但会增加一些判断语句,增加代码编写和理解的难度,丢失可读性。在这里不做状态压缩。
下面是编码的时候要注意的事项:总是先得到小子串的回文判定,然后大子串才能参考小子串的判断结果。
思路是:
1、在子串右边界 j 逐渐扩大的过程中,枚举左边界可能出现的位置;
2、左边界枚举的时候可以从小到大,也可以从大到小。
这两版代码的差别仅在内层循环,希望大家能够自己动手,画一下表格,思考为什么这两种代码都是可行的,相信会对“动态规划”作为一种“表格法”有一个更好的理解。
作者:liweiwei1419
链接:https://leetcode-cn.com/problems/longest-palindromic-substring/solution/zhong-xin-kuo-san-dong-tai-gui-hua-by-liweiwei1419/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
/*
* 给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2:
输入: "cbbd"
输出: "bb"
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-palindromic-substring
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
*/
public class Lc5 {
public static String longestPalindrome(String s) {
int len = s.length();
// ·只有一个字符串
if (len < 2) {
return s;
}
char ch[] = s.toCharArray();
boolean[][] dp = new boolean[len][len];
for (int i = 0; i < dp.length; i++) {
dp[i][i] = true;
}
int maxlen = 1;
int start = 0;
for (int j = 1; j < ch.length; j++) {
for (int i = j - 1; i >= 0; i--) {
if (ch[i] == ch[j]) {
// ·回文字符串最中间的一个/俩个字符
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
} else {
dp[i][j] = false;
}
//·只有变更最长长度是才会重新定义起始位置下标
if (dp[i][j]) {
if (maxlen < (j - i + 1)) {
maxlen = j - i + 1;
start = i;
}
}
}
}
return s.substring(start, start + maxlen);
}
public static void main(String[] args) {
String s = "abadd";
System.out.println(longestPalindrome(s));
}
}
原文:https://www.cnblogs.com/xiaoshahai/p/12152460.html