leetcode教程系列——Binary Tree

　　tree是一种常用的数据结构用来模拟真实物理世界里树的层级结构。每个tree有一个根(root)节点和指向其他节点的叶子(leaf)节点。从graph的角度看，tree也可以看作是有N个节点和N-1个边的有向无环图。

　　Binary tree是一个最典型的树结构。顾名思义，二分数的每个节点最多有两个children，分别叫左叶子节点与右叶子节点。下面的内容可以让你学习到：

1. 理解tree的概念以及binary tree
2. 熟悉不同的遍历方法
3. 使用递归来解决二分树相关的问题

A. 遍历一棵树

• Pre-order Traversal
• In-order Traversal
• Post-order Traversal
• Recursive or Iterative

　　1. Pre-order Traversal（前序遍历）: 也就是先访问根节点，然后访问左叶子节点与右叶子节点

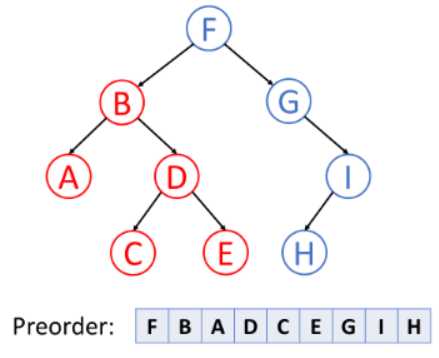
　　2. In-order Traversal（中序遍历）：先访问左叶子节点，接着访问根节点，最后访问右叶子节点

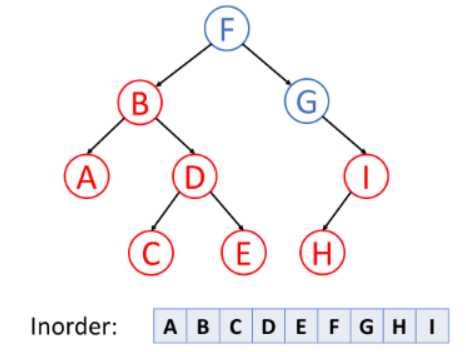
 　　3. Post-order Traversal （后序遍历）：先访问左叶子节点，再访问右叶子节点，最后访问根节点

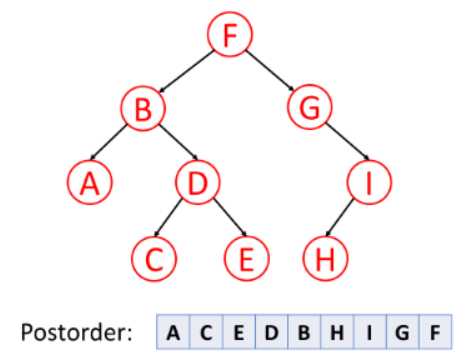
值得注意的是当你删除树的某一个节点时，删除流程应该是post-order（后序）的。也就是说删除一个节点前应该先删除左节点再删除右节点，最后再删除节点本身。

post-order被广泛使用再数学表达式上。比较容易来写程序来解析post-order的表达式，就像下面这种：

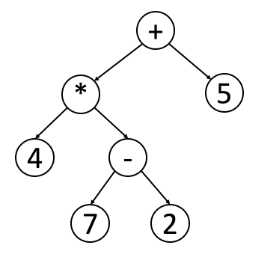
使用in-order遍历能够很容易搞清楚原始表达但是不容易处理表达式，因为需要解决运算优先级的问题。

如果使用post-order的话就很容易使用堆栈来解决这个表达。 每个碰到一个运算符的时候就pop两个元素出来计算结果然后再压入栈。

下面来做几个题目：

1.

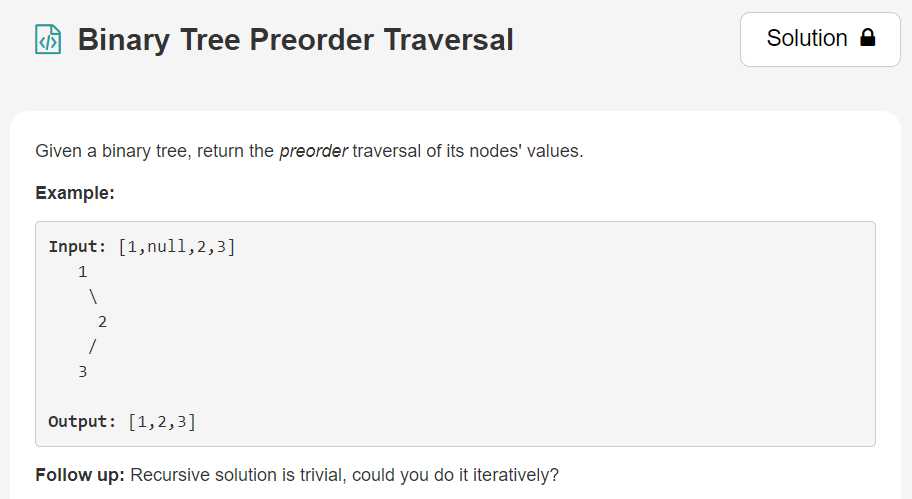
link:[https://leetcode.com/explore/learn/card/data-structure-tree/134/traverse-a-tree/928/]

 递归解法：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    
    def solve(self,root):
        if root is not None:
            self.result.append(root.val)
            self.solve(root.left)
            self.solve(root.right)
        return self.result
    
    def preorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        self.result=[]
        self.solve(root)
        return self.result

循环解法：

leetcode教程系列——Binary Tree

原文：https://www.cnblogs.com/Thinker-pcw/p/12161673.html