决策树: if-then 规则的集合
性质:互斥并且完备,每个实例有且仅有一条对应的规则或者路径
决策树表示给定特定特征条件下的条件概率分布
条件概率分布将特征空间进行了划分,每个划分是一个单元或者区域
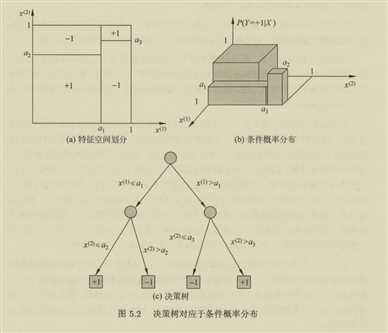
决策树学习的本质是从训练数据集中归纳一组分类规则
损失函数通常是正则化的极大似然函数
损失函数确定,学习问题变为找到损失函数意义下的最优决策函数,(NP)问题,通常使用启发算法,求近似解
\[g(D,A) = H(D)-H(D|A)\]
信息增益等价于互信息
\(H(D) = -\sum_{k} \frac{|D_k|}{|D|}log_2{\frac{|D_k|}{|D|}}\)
\(H(D|A) = -\sum_{i=1}^{n}\frac{|D_i|}{|D|}H(D_i)=-\sum_{i=1}^{n}\frac{|D_i|}{|D|}\sum_{k}\frac{|D_{ik}|}{|D|}log_2{\frac{|D_{ik}|}{|D|}}\)
使用信息增益选择特征偏向于特征值较多的特征
\[g_R(D,A) = \frac{g(D,A)}{H_A(D)}\]
\[H_A(D) = -\sum_{i=1}^{n}\frac{|D_i|}{|D|}log_2{\frac{|D_i|}{|D|}}\]


防止过拟合,提高模型的泛化能力
树\(T\),的叶节点\(|T|\),\(t\)是树\(T\)的叶节点,该叶节点有\(N_t\)个样本点,其中\(k\)类的样本点有\(N_{tk}\),\(H_t(T)\)为叶节点\(t\)上的经验熵
损失函数
\[C_\alpha(T) = \sum_{t=1}^{|T|} N_tH_t(T)+\alpha |T|\]
\[H_t(T) = -\sum_{k} \frac{N_{tk}}{N_t} log_2{\frac{N_{tk}}{N_t}}\]
\[C(T) = \sum_{t=1}^{|T|} N_tH_t(T)\]
\[C_\alpha(T) = C(T)+\alpha|T|\]
分类与回归树(classification and regression tree)

基尼指数
\[Gini(p) = \sum_{k}(1-p_k)p_k = 1-\sum_{k}p_k^2\]
\[Gini(D) = 1-\sum_{k=1}^{K} (\frac{|D_k|}{|D|})^2\]
二分类决策树
\[Gini(D,A) = \frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2)\]
\(\alpha\)控制者模型的大小,所以希望通过不同的\(\alpha\)来找到不同的大小的模型,然后通过交叉验证获取最好的模型
问题是\(\alpha\)如何选择
对于树中的一个内部节点\(t\),以t为单节点的损失函数(意味着在t节点剪纸后的结果)
\(C_\alpha(t) = C(t)+\alpha\)
以\(t\)为根节点的子树\(T_t\)的损失函数
\(C_\alpha(T_t) = C(T_t)+\alpha |T_t|\)
当\(\alpha=0\)的时候\(C_\alpha(T_t)< C_\alpha(t)\)
当\(\alpha \to \infty\),\(C_\alpha(T_t)>C_\alpha(t)\)
连续函数,零点存在定理,存在\(\alpha=\frac{C(t)-C(T_t)}{|T_t|-1}\),时相同的损失函数.但是t的节点更少,t比\(T_t\)更可取.对\(T_t\)剪纸

原文:https://www.cnblogs.com/Lzqayx/p/12171733.html