Jodie慢慢地步入实验室,跟随在她身旁的灵体Aiden似乎有点不高兴,但还是形影不离地跟随着Jodie。
今天Jodie要进行的实验在一个很大很大的圆环上面,圆环上有L个格子,每个格子上都显示着一个小写英文字母,Jodie从任意格子开始当她离开一个格子的时候那个格子的字母就会改变,这个改变是随机的,没有人知道会变成什么。Jodie在这个环上不回头顺时针地走,每进入一个格子就会在本子上写下这个格子当前显示的字母。由于Jodie不能回头而且不知道这个圆环上有多少个格子,她并不知道自己什么时候会走到重复的点,所以她让Aiden在她下一步走进重复格子的时候提醒一下。但可能他们闹了矛盾,Aiden发了脾气,决定在Jodie走了K(K\geq 0K≥0)步重复的格子之后才告诉她。Jodie进行了两次实验,记录了两次走的路径。第二次实验再进去之前,每个格子所显示的字母会被重设为第一次实验开始前的样子。Jodie发现了Aiden的恶作剧,她只能把可能的最大的L告诉实验人员。
为了帮助你更好的理解题目,请仔细分析一下例子:
假设L = 4,K = 1
第一次实验开始前每个格子显示的字母如下图:
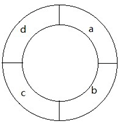
Jodie从显示字母为’a’的格子开始走,Aiden在她走了K步重复的格子之后告诉她停止,所以Jodie一共走了5步,每走一步,格子的变化如下(箭头指着Jodie所在的格子):
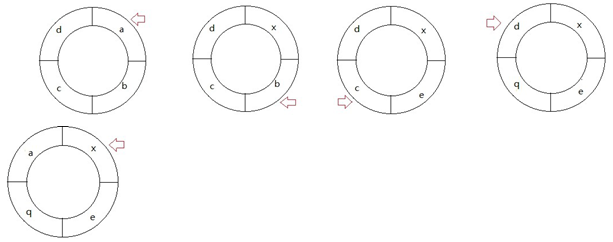
Jodie的第二次实验从显示字母为’c’的格子开始走,每走一步格子的变化如下(箭头指着Jodie所在的格子):
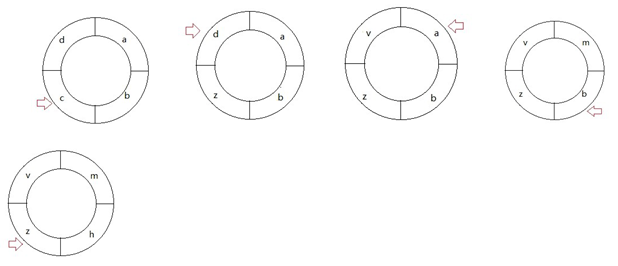
Jodie两次实验记录的路径分别为:
“abcdx”
“cdabz”
现在给出Jodie记录的两次路径的长度N,以及Jodie所写的内容,但是并不知道K是多少,希望你能帮忙求出一个最大的可能的L。
注:题目背景是Beyond: Two Souls
令第一个字符串为S,第二个字符串为T。前i个格子能构成一个环,当且仅当存在\(j\)使得\(S[j,i]\)和\(T[1,i-j+1]\) 相等, \(S[1,j-1]\)和\(T[i-j+2,i]\)相等。
发现前半部分很像S的一个后缀和T的公共前缀,可以用扩展KMP求解。后半部分同理。因此,我们运用扩展KMP求出S和T以及T和S匹配的extend数组,记为\(f_1,f_2\)
我们枚举\(j\),上面提到的第一段\(S[j,i]\)对应的是\(T[1,f_1[j]]\),\(i=j+f_1[j]+1\).然后考虑第2段,\(T[f_1[j]+1]\)及之后的部分应该和\(S[1,j-1]\)匹配。因此\(f_2[f_1[j]+1] \geq j-1\).那么只要\(f_2[f_1[j]+1] \geq j-1\),我们用就用\(j+f_1[j]+1\)更新答案即可
#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 2000000
using namespace std;
int n;
char s[maxn+5],t[maxn+5];
void get_nex(char *t,int m,int *nex){
nex[1]=m;
nex[2]=0;
while(t[2+nex[2]]==t[1+nex[2]]) nex[2]++;
for(int i=3,p0=2,r=p0+nex[p0]-1;i<=m;i++){
if(i+nex[i-p0+1]-1<r) nex[i]=nex[i-p0+1];
else{
nex[i]=max(r-i+1,0);
while(t[i+nex[i]]==t[1+nex[i]]) nex[i]++;
p0=i;
r=i+nex[i]-1;
}
}
}
void get_extend(char *s,int n,char *t,int m,int *extend){
static int nex[maxn+5];
get_nex(t,m,nex);
// for(int i=1;i<=m;i++) printf("%d ",nex[i]);
// printf("\n");
extend[1]=0;
while(s[extend[1]+1]==t[extend[1]+1]) extend[1]++;
for(int i=2,p0=1,r=p0+extend[p0]-1;i<=n;i++){
if(i+nex[i-p0+1]-1<r) extend[i]=nex[i-p0+1];
else{
extend[i]=max(r-i+1,0);
while(s[i+extend[i]]==t[1+extend[i]]) extend[i]++;
p0=i;
r=i+extend[i]-1;
}
}
}
int f1[maxn+5],f2[maxn+5];
int main(){
scanf("%d",&n);
scanf("%s",s+1);
scanf("%s",t+1);
n=strlen(s+1);
get_extend(s,n,t,n,f1);
get_extend(t,n,s,n,f2);
int ans=0;
for(int i=1;i<=n;i++){
if(f2[f1[i]+1]>=i-1) ans=max(ans,i+f1[i]-1);
}
if(ans==38928) ans=55851;
printf("%d\n",ans);
} 原文:https://www.cnblogs.com/birchtree/p/12172148.html