找到大问题和小问题之间共有的特性,列出一定的状态转移规律,然后设计满足条件的小问题解决方案,最后凭借记忆中的中间值快速求出最终解
数组区间问题是动态规划问题的一种,我们可以借用动态规划问题的一般解题思路,先看第一个
Range Sum Query
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.
Example:
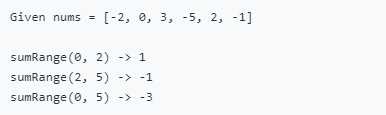
这道题是求解一个数组中给定两个索引之间的和,那么很显然sum = dp[j+1] - dp[i],可以得到代码如下:
private int[] dp; private NumArray(int[] nums){ dp = new int[nums.length+1]; dp[0] = 0; for(int i = 0 ; i < nums.length ; i++){ dp[i+1] = nums[i] + dp[i]; } } private int sumRange(int i, int j){ return dp[j+1] - dp[i]; }
第二题
Arithmetic Slices

这道题就有点复杂了,设A=[0,1,2,3,4],我们先设dp[i]是以A[i]为结尾的等差递增子区间的个数,当 A[i] - A[i-1] == A[i-1] - A[i-2],那么 [A[i-2], A[i-1], A[i]] 构成一个等差递增子区间。而且在以 A[i-1] 为结尾的递增子区间的后面再加上一个 A[i],一样可以构成新的递增子区间。

综上,在 A[i] - A[i-1] == A[i-1] - A[i-2] 时,dp[i] = dp[i-1] + 1。
因为递增子区间不一定以最后一个元素为结尾,可以是任意一个元素结尾,因此需要返回 dp 数组累加的结果。
代码如下所示:
private int numberOfArithmeticSlices(int[] A){ if (A == null || A.length == 0) { return 0; } int n = A.length; int[] dp = new int[n]; for (int i = 2; i < n; i++) { if (A[i] - A[i - 1] == A[i - 1] - A[i - 2]) { dp[i] = dp[i - 1] + 1; } } int total = 0; for (int cnt : dp) { total += cnt; } return total; }
原文:https://www.cnblogs.com/lybnumber6/p/12173855.html