1. 矩阵分解可以用来解决什么方法, 以及how?
利用矩阵分解来解决实际问题的分析方法很多，如PCA(主成分分析)、ICA(独立成分分析)、SVD(奇异值分解)、VQ(矢量量化)等。在所有这些方法中，原始的大矩阵V被近似分解为低秩的V=WH形式。这些方法的共同特点是，因子W和H中的元素可为正或负，即使输入的初始矩阵元素是全正的，传统的秩削减算法也不能保证原始数据的非负性。在数学上，从计算的观点看，分解结果中存在负值是正确的，但负值元素在实际问题中往往是没有意义的。例如图像数据中不可能有负值的像素点；在文档统计中，负值也是无法解释的。
2. NMF
NMF的基本思想可以简单描述为：对于任意给定的一个非负矩阵A，NMF算法能够寻找到一个非负矩阵U和一个非负矩阵V，使得满足 ，从而将一个非负的矩阵分解为左右两个非负矩阵的乘积。
分解前后可理解为：原始矩阵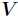
的列向量是对左矩阵
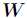中所有列向量的加权和，而权重系数就是右矩阵对应列向量的元素，故称
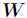为基矩阵，
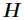为系数矩阵。一般情况下
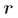的选择要比
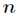小，即满足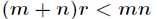
，这时用系数矩阵代替原始矩阵，就可以实现对原始矩阵进行降维，得到数据特征的降维矩阵，从而减少存储空间，减少计算机资源。
other documentations: NMF 非负矩阵分解 -- 原理与应用
Supplementary knowledge
NMF: non-negative matrix factorization.
原文：https://www.cnblogs.com/dulun/p/12178269.html