蒙特卡洛积分法（二）

上一次我们谈到，使用蒙特卡洛积分法求积分涉及到两个问题：1.如何对一个任意分布函数进行抽样； 2.如何减少方差。这里我们先来探讨第一个问题，给定一个概率密度函数，如何对其进行采样，使采样满足其概率分布。
平常有两种方法实现：

1.逆变换算法

假设我们有一个概率分布函数p(x)，对它取积分，可以得到它累积分布函数P(x)，这个函数根据性质我们知道它的值域是一定分布在[0,1]区间的。那么通过它的反函数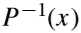就可以实现输入[0,1]之间的随机数，得到符合概率密度分布的采样点。
我们可以从一个离散分布的图像中来加深理解，下图是一个离散分布函数p(x)：

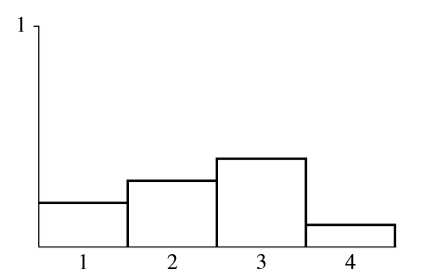
它的累积分布函数如下：

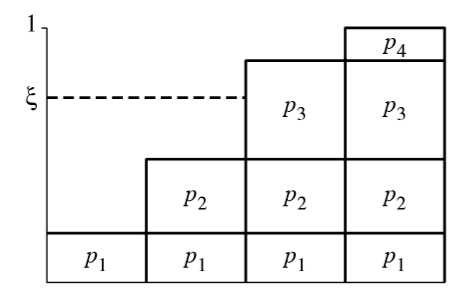
可以看到，当我们取值域上的一点ξ，它对应的定义域值为3。p(3)的值较大，因此它也就有更多几率被采样到。也就是说对于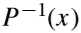，输入一个均匀采样的[0,1]值，就可以得到符合p(x)概率分布的定义域采样点。
因此逆变换算法的过程如下：
1.首先计算p(x)的累积分布函数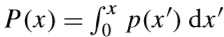
2.计算累积分布函数的反函数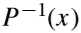
3.然后在[0,1]均匀分布随机产生一个随机数ξ
4.最后将ξ带入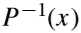中求出满足p(x)分布的随机数。

2.取舍算法

当累计分布函数或其反函数没有显示的解析表达式，或者概率密度函数没有边界，不能归一化的时候，逆变换算法就无法使用，此时应当使用取舍算法。

蒙特卡洛积分法（二）

原文：https://www.cnblogs.com/wickedpriest/p/12179984.html