背包问题(Knapsack problem)可以描述为:给定一组物品,每种物品都有自己的价格和价值,在限定的总价格内,我们如何选择,才能使得物品的总价值最高。
01背包指的就是每件物品要么选,要么不选。如果选,只能选一件。
先来分析一下01背包的特征。结果我们发现01背包具有最优子结构(自己去查这是什么意思)。有最有子结构的问题自然要用动态规划来解。
说道动态规划,就一定要有动态转移方程。
第一件事就是确定转移方程的维度。容易看出,转移方程有两个维度,分别是价值和价格。
接下来就是确定转移方程。我们先考虑在空间为m,有n-1件物品时的最优解,然后判断选或不选第n件物品的价值,取最大值作为f(n, m)的值。可得转移式为
f(n,m)=max?{ f(n-1,m),f(n-1,m-w[n])+v[n] }
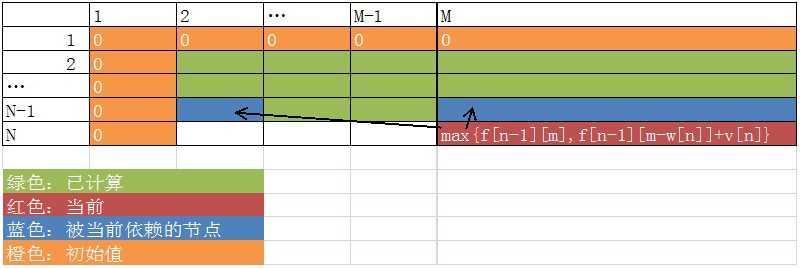
其实这个时候就可以求解01背包了。但是二维的转移矩阵往往出现爆空间的情况。于是就要进行优化。
由上表和转移矩阵可以得出当前节点只会依赖到上面一行的数据,这样就可以吧二维数组压缩到两个一维数组。像放鞭炮一样往下放。
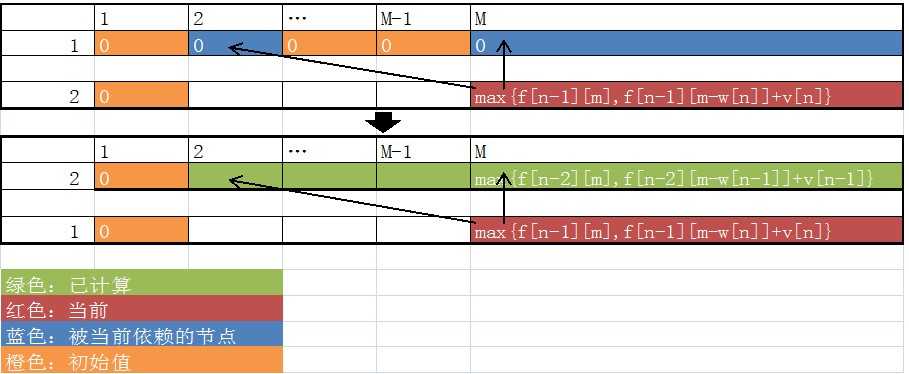
这样其实已经很好了,空间被优化成线性。但是这样做有一个缺点,就是两个数组来回倒会大大增加代码的长度和调试时间。那把数组直接优化成一维不就好了吗?可以的。因为我们发现,当前格子只可能依赖到自己上面和左边的格子,不可能依赖到自己右面的格子。
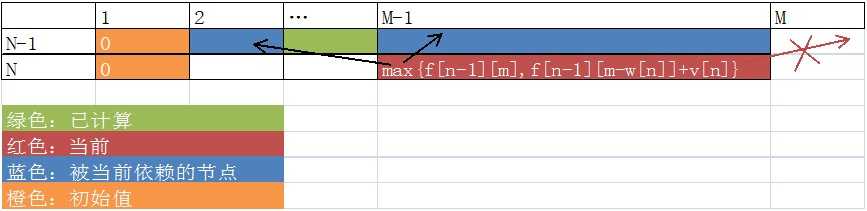
那么就可以把数组压缩成一维的。但是计算要逆序,不然就会覆盖掉上次的计算结果,导致计算出错。
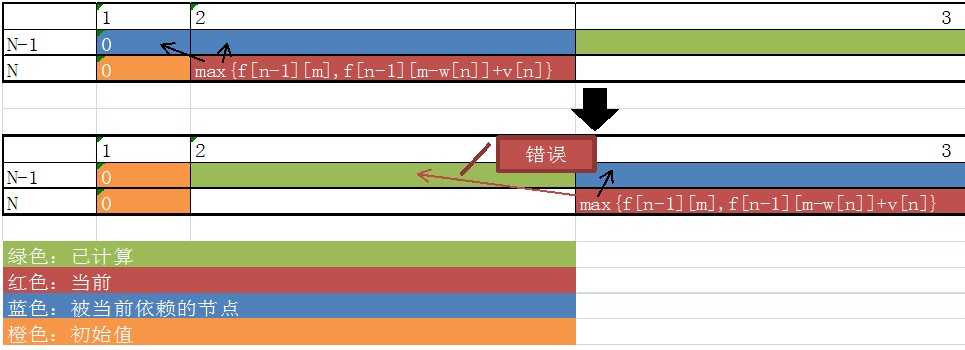
此时,转移方程就变成了
f(m)=max?{ f(m),f(m-w[n])+v[n] }
再次强调,v要逆序!像这样:
1. memset(f,0,sizeof f); 2. for (int n = 0; n < N; ++n) { 3. for (int m = M; M >= 0; ++m) { 4. f[m] = max(f[m], f[m - w[n]] + v[n]) 5. } 6. }
原文:https://www.cnblogs.com/Iuppiter/p/12183181.html