最近zkx大佬在学图论,有一些定义很秀,压根读不懂,所以按照自己的理解来总结一下。
图:将点用边连起来,点与边共同组成图。
下面这两个都是图。
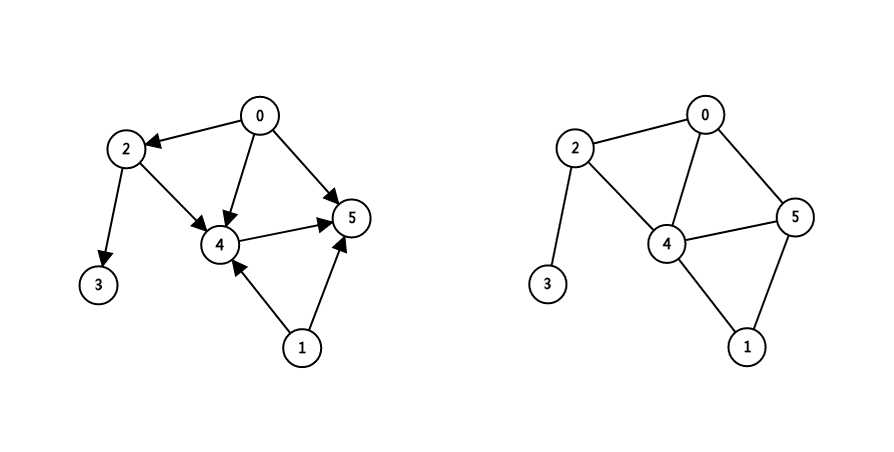
有向图:连接点的边有方向(只能按照边的方向走)。
上面的左图就是有向图。
无向图:连接点的边没有方向(相当于两条反向的有向边)。
上面的右图就是无向图。
顶点集合:是原图中 点 的集合。
割点集合:是个 顶点集合,在原 连通图 中删去 集合中的所有的点 和 与集合中的点相连的边 后,原 连通图 不再连通。
点连通度:最小 的 割点集合 的大小(最小的割点集合中的点的个数)。
割边集合:是个 边 的集合,在原 连通图 中删去 集合中所有的边 后,原 连通图 不再连通。
边连通度:最小 的 割边集合 的大小(最小的割边集合中边的个数)。
割点:一个 点,使得在原 连通图 中删去该点后原 连通图 不再连通,很明显只有当该图的 点连通度 为 \(1\) 时,该图才存在割点。
原文:https://www.cnblogs.com/poi-bolg-poi/p/12183166.html