前文:在经历了几天的刷二分和图论后,我开始打起了数据结构,有感写下了这篇博文 QWQ
首先,我们来看看树状数组是什么东西 (出自百度)
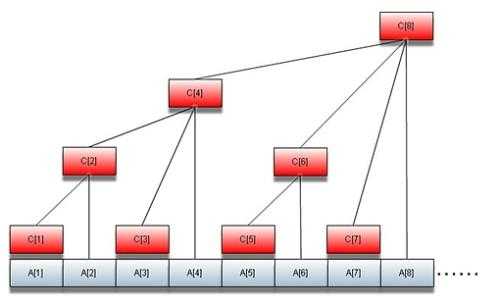
大概就是这个亚子
从图中我们可以看出,有A和C 2个数组,其中A是存储整个序列的数组,而C是线段树数组
再来看每一个节点——树状数组的每一个节点的分布好像并无规律,实际上是有的,对于一个节点i,图中的一层一层其实就是它的lowbit ,这个大概知道一下就好了
inline int lowbit (int x) { return x&(-x); }
上面的代码会打就好
好,接下来我们来看 lowbit=1的节点有 1,3,5,7 而他们没有子树 说明他们存储的是A[i]这个元素的值
lowbit=2 2,6 节点2储存的值为C[1]+A[2] 节点6储存的值为C[5]+A[6]
lowbit=3 4 储存的值为C[2]+C[3]+A[4]
先弃坑,,,,,有空慢慢填
树状数组1代码 https://www.luogu.com.cn/problem/P3374
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #define MAX 500233 #define int long long int n,m; int tree[MAX],a[MAX]; inline int lowbit (int x) { return x&(-x); } inline void updata(int x,int k) { for(;x<=n;x+=lowbit(x)) tree[x]+=k; } inline int query(int x) { int answ=0; while(x!=0) { answ+=tree[x]; x-=lowbit(x); } return answ; } signed main() { scanf("%lld%lld",&n,&m); for(int i=1;i<=n;i++) { scanf("%lld",&a[i]); updata(i,a[i]); } int qwq,tat,qaq; while(m--) { scanf("%lld%lld%lld",&qwq,&tat,&qaq); if(qwq==1) updata(tat,qaq); else printf("%lld\n",query(qaq)-query(tat-1)); } return 0; }
线段树1代码
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #define MAX (int)(1e5+10) #define int long long int ans[MAX<<2],tag[MAX<<2]; void lazyadd(int l,int r,int qq,int k) { ans[qq]+=(r-l+1)*k; tag[qq]+=k; } #define mid ((l+r)>>1) #define leftson (cur<<1) #define rightson ((cur<<1)|1) #define push_up ans[cur]=ans[leftson]+ans[rightson] #define push_down lazyadd(l,mid,leftson,tag[cur]); lazyadd(mid+1,r,rightson,tag[cur]); tag[cur]=0; using namespace std; void build(int cur,int l,int r) { if(l==r) { scanf("%lld",&ans[cur]); return; } build(leftson,l,mid); build(rightson,mid+1,r); push_up; } int _(int cl,int cr,int l,int r,int cur) { int answ=0; if(cl<=l&&r<=cr) { return ans[cur]; } push_down; if(cl<=mid) answ+=_(cl,cr,l,mid,leftson); if(cr>=mid+1) answ+=_(cl,cr,mid+1,r,rightson); return answ; } void insert(int ql,int qr,int l,int r,int cur,int del) { if(ql<=l&&r<=qr) { ans[cur]+=(r-l+1)*del; tag[cur]+=del; return; } push_down; if(ql<=mid) insert(ql,qr,l,mid,leftson,del); if(qr>=mid+1) insert(ql,qr,mid+1,r,rightson,del); push_up; } signed main() { int n,m; scanf("%lld%lld",&n,&m); int qqq,x,y,k; build(1,1,n); for(int i=0;i<m;i++) { scanf("%lld",&qqq); if(qqq==1) { scanf("%lld%lld%lld",&x,&y,&k); insert(x,y,1,n,1,k); } else { scanf("%lld%lld",&x,&y); printf("%lld\n",_(x,y,1,n,1)); } } return 0; }
树状数组2代码
#include <cstdio> #include <algorithm> #define MAXN 5000010 #define int long long using namespace std; int a[MAXN]; //维护的是一个差分数组 int n,m,x,y,k,opt; int lowbit(int x) { return x&(-x); } void add(int s,int x) { for(;s<=n;s+=lowbit(s)) a[s]+=x; } int ask(int x) { int ans=0; while(x) { ans+=a[x]; x-=lowbit(x); } return ans; } signed main() { scanf("%lld%lld",&n,&m); int la=0,no; for(int i=1;i<=n;i++) { scanf("%lld",&no); add(i,no-la); la=no; } for(int i=1;i<=m;i++) { scanf("%lld",&opt); if(opt==1) { scanf("%lld%lld%lld",&x,&y,&k); add(x,k); add(y+1,-k); } else { scanf("%lld",&k); printf("%lld\n",ask(k)); } } }
线段树2代码
#include <cstdio> #include <algorithm> #define ll long long #define MAXN (int)(1e5+20) #define mid ((l+r)>>1) #define ls (cur<<1) #define rs (ls|1) ll n,m,p; ll a[MAXN]; ll sum[MAXN<<2],add[MAXN<<2],mul[MAXN<<2]; using namespace std; void push_up(ll cur) { sum[cur]=(sum[ls]+sum[rs])%p; } void push_down(ll cur,ll l,ll r) { sum[ls]=(sum[ls]*mul[cur])%p; sum[rs]=(sum[rs]*mul[cur])%p; sum[ls]=(sum[ls]+(add[cur]*(mid-l+1)))%p; sum[rs]=(sum[rs]+(add[cur]*(r-mid)))%p; mul[ls]=(mul[ls]*mul[cur])%p; mul[rs]=(mul[rs]*mul[cur])%p; add[ls]=(add[ls]*mul[cur])%p; add[rs]=(add[rs]*mul[cur])%p; add[ls]=(add[ls]+add[cur])%p; add[rs]=(add[rs]+add[cur])%p; add[cur]=0; mul[cur]=1; } void build(ll cur,ll l,ll r) { mul[cur]=1; //把一路的乘法标记清为1 if(l==r) { sum[cur]=a[l]%p; return; } build(ls,l,mid); build(rs,mid+1,r); push_up(cur); } void addjia(ll cur,ll cl,ll cr,ll l,ll r,ll k) { if(cl<=l&&r<=cr) { add[cur]=(add[cur]+k)%p; sum[cur]=(sum[cur]+(k*(r-l+1)))%p; return; } push_down(cur,l,r); if(cl<=mid) addjia(ls,cl,cr,l,mid,k); if(cr>mid) addjia(rs,cl,cr,mid+1,r,k); push_up(cur); } void addcheng(ll cur,ll cl,ll cr,ll l,ll r,ll k) { if(cl<=l&&r<=cr) { add[cur]=(add[cur]*k)%p; mul[cur]=(mul[cur]*k)%p; sum[cur]=(sum[cur]*k)%p; return; } push_down(cur,l,r); if(cl<=mid) addcheng(ls,cl,cr,l,mid,k); if(cr>mid) addcheng(rs,cl,cr,mid+1,r,k); push_up(cur); } ll query(ll cur,ll cl,ll cr,ll l,ll r) { if(cl<=l&&r<=cr) return sum[cur]; push_down(cur,l,r); ll answ=0; if(cl<=mid) answ=(answ+query(ls,cl,cr,l,mid))%p; if(cr>mid) answ=(answ+query(rs,cl,cr,mid+1,r))%p; return answ%p; } void debug(ll cur,ll l,ll r) { if(l==r) { printf(":%d ",sum[cur]); return; } debug(ls,l,mid); debug(rs,mid+1,r); } ll read() { char ch; ll an=0; int ok=1; ch=getchar(); while(ch>‘9‘||ch<‘0‘) ch==‘-‘?ok=-1:ok=1,ch=getchar(); while(ch<=‘9‘&&ch>=‘0‘) an=(an<<3)+(an<<1)+(ch-‘0‘),ch=getchar(); return an*ok; } int main() { n=read(); m=read(); p=read(); for(int i=1;i<=n;i++) a[i]=read(); build(1,1,n); ll x,y,z,opt; for(int i=1;i<=m;i++) { opt=read(); x=read(); y=read(); if(opt==1) { z=read(); addcheng(1,x,y,1,n,z); } else if(opt==2) { z=read(); addjia(1,x,y,1,n,z); } else { printf("%lld\n",query(1,x,y,1,n)%p); } // debug(1,1,n); } }
原文:https://www.cnblogs.com/xugangfan/p/12188974.html