[BZOJ-1005&洛谷P2624][HNOI2008]明明的烦恼-【Purfer序列】py+java-布布扣-bubuko.com

HINT

　　两棵树分别为1-2-3;1-3-2

相较于04年的裸的Purfer序列，这题就不是那么裸了。

假设有k个是已知的度，那么根据Purfer序列的性质我们可以得到这k个已知度的答案：

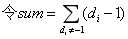
技术分享图片

那么该部分的答案应该为：

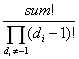
技术分享图片

但由于purfer中有n-2个元素，那么这sum个元素的放置方法也有C（n-2,sum）种，即该部分的最终答案为：

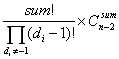
技术分享图片

然后就是剩下的了，剩下的有n-k个顶点，序列空余n-2-sum个位置，那么每个顶点有n-2-sum中放法，即有

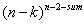技术分享图片种答案。

那么最终答案也就出来了：

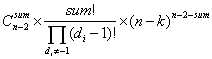
技术分享图片

emmmm，还是py一波+JAVA一波吧。。

以下是AC代码：（Python）

n=int(input())
a=[]
for i in range(n):
    a.append(int(input()))
sum=0;k=0
for i in range(n):
    if a[i]!=-1:
        sum+=a[i]-1
        k+=1
    elif a[i]==0:
        print(0)
        exit()

c=1
for i in range(n-2-sum+1,n-2+1):
    c*=i
for i in range(2,sum+1):
    c//=i

tot=1
f=[1]
for i in range(1,sum+1):
    tot*=i
    f.append(f[i-1]*i)
for i in range(n):
    if a[i]!=-1:
        tot//=f[a[i]-1]

last=1;
for i in range(n-2-sum):
    last*=(n-k)

print(c*tot*last)

（Java代码）：

import java.math.BigInteger;
import java.util.Scanner;

class Main {
    public static void main(String[] args){
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        int a[]=new int[1005];
        int mark=0,sum=0,k=0;
        for (int i=1; i<=n; i++){
            a[i]=sc.nextInt();
            if (a[i]==0) mark=1;
            if (a[i]!=-1) {
                sum+=a[i]-1;k++;
            }
        }
        if (mark==1) {
            System.out.println("0");
            System.exit(0);
        }
        BigInteger s=new BigInteger("1");
        BigInteger num[]=new BigInteger[1005];
        num[0]=new BigInteger("0");
        int mx=n;
        if (sum>n) mx=sum;
        for (int i=1; i<=mx; i++)
            num[i]=num[i-1].add(new BigInteger("1"));
        for (int i=n-2; i>=n-2-sum+1; i--)
            s=s.multiply(num[i]);
        for (int i=2; i<=sum; i++)
            s=s.divide(num[i]);
        BigInteger tot=new BigInteger("1");
        for (int i=1; i<=sum; i++)
            tot=tot.multiply(num[i]);
        BigInteger f[]=new BigInteger[1050];
        f[0]=new BigInteger("1");
        for (int i=1; i<=n; i++)
            f[i]=f[i-1].multiply(num[i]);
        BigInteger cnt=new BigInteger("1");
        for (int i=1; i<=n; i++)
            if (a[i]!=-1)  cnt=cnt.multiply(f[a[i]-1]);
        BigInteger last=new BigInteger("0");
        for (int i=1; i<=n-k; i++) last=last.add(new BigInteger("1"));
        BigInteger tot_last=new BigInteger("1");
        for (int i=1; i<=n-2-sum; i++) tot_last=tot_last.multiply(last);
        System.out.println(s.multiply(tot.divide(cnt)).multiply(tot_last));
    }
}

原文：https://www.cnblogs.com/lonely-wind-/p/12189938.html

[BZOJ-1005&洛谷P2624][HNOI2008]明明的烦恼-【Purfer序列】py+java

Description

Input

Output

Sample Input

Sample Output

HINT