任务目的：
1.理解K对模型的影响
2.如何得到最好的k值
3.如何让knn减少隐患（更标准化）
一、KNN的决策边界以及K的影响
决策依据于的某个边界，在knn中则是用来区分不同类的点的分类边界。随着k值的上升，决策边界也就越趋于平滑。如下图：
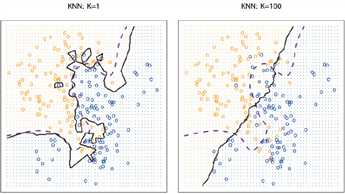
紫色那条是最佳分类边界线，黑色的是knn的边界线，可以看出k越大，决策边界线越平滑。
那是不是越平滑模型准确率就越高勒？——不是的，越平滑就代表风险越小，收益也越小，所以我们要平衡。当k过大时，意味着离待分类样本点较远的点也会被包含进来对其判别产生影响，此时就会欠拟合。
二、交叉验证
核心思想：一个一个试，然后选出效果最好的K值。
内容:将训练数据分出一个区域为验证数据，K折交叉验证，就是将所有训练集分成K块（这里的k和knn的k是两个概念），依次用验证数据验证k值。
训练集用于训练模型。
验证集用于模型的参数选择配置。（在此处就是在配置knn的k参数了）
测试集对于模型来说是未知数据，用于评估模型的泛化能力。
k折交叉验证具体做法：
第一步，不重复抽样将原始数据随机分为 k 份。
第二步，每一次挑选其中 1 份作为测试集，剩余 k-1 份作为训练集用于模型训练。
第三步，重复第二步 k 次，这样每个子集都有一次机会作为测试集，其余机会作为训练集。
第四步，计算 k 组测试结果的平均值作为模型精度的估计，并作为当前 k 折交叉验证下模型的性能指标。
代码（使用sklearn)：
1 import numpy as np
2 from sklearn import datasets
3 from sklearn.neighbors import KNeighborsClassifier
4 from sklearn.model_selection import KFold
5 from sklearn.model_selection import GridSearchCV
6
7 iris = datasets.load_iris()
8 X = iris.data
9 y = iris.target
10
11 k_range = list(range(1,16,2)) #range函数（开始，结束，步长）
12 param_gridknn = dict(n_neighbors = k_range)
13 knn = KNeighborsClassifier()
14
15 clf = GridSearchCV(knn, param_gridknn, cv = 5)
16 clf.fit(X, y)
17
18 print("best score is : %.2f" % clf.best_score_, "best param : ", clf.best_params_)
刚学完k折交叉验证，突然发现这和最近的一场cf的一道交互题的思维非常相似qaq。
题干：http://codeforces.com/contest/1270/problem/D
题意：有一个长度为n的序列，下标从1到n，你每次可以进行一次询问，对交互机输入m个下标，它返回给你第k小的元素的下标，最多询问n次，通过返回的信息确定那个参数k！
分析：相对于knn确定参数k，这里也是要确定参数k，对于m个元素的集合，因为它给我们的返回的信息非常少，所以我们使询问区间的交集尽可能大，对于序列中的m+1个元素的子集，我们每次选取m个作为询问，这样就可以询问m+1次，每个元素只有一次不加入询问集合，其余m次都在询问区间，然后我们得到m组的"测试结果“，通过一定找规律就能通过测试集了（指AC，手动纪念把ACM和机器学习结合，虽然稍微有点扯，( •? ω •? )y）。
欧式距离的隐患是：当一个坐标系的计量单位发生过大改变时，会使得knn距离计算中一个坐标会起到很大的作用，另一个坐标没啥用了。
不同属性有不同量级会导致：
1.数量级的差异将导致量级较大的属性占据主导地位。
2.数量级的差异将导致迭代收敛速度减慢。
3.依赖于样本距离的算法对于数据的数量级非常敏感。
解决办法->特征标准化
分为线性归一化和标准差归一化。
前者指的是把特征值的范围映射到[0,1]区间，后者的方法使得把特征值映射到均值为0，标准差为1的高斯分布。
前者：
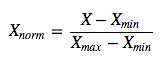
后者：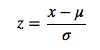 
其中，μ、σ分别为原始数据集的均值和标准差。
这样我们就能有效解决坐标维度量级差别带来的影响，具体哪个归一办法好得都试试。
参考博客：
https://www.cnblogs.com/sddai/p/8379452.html
https://blog.csdn.net/bohu83/article/details/93422797
原文：https://www.cnblogs.com/qq2210446939/p/12189500.html