博弈的要素：
这是第一次接触正式的博弈论知识
策略形式书面定义为：行为影响结果，然而结果不仅取决你的行为，还取决与其他人的行为。
课本
杜塔的《策略与博弈》，乔尔·沃森的《策略》还有另外一本《战略思想》
第一个游戏
囚徒困境
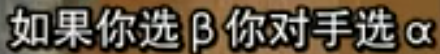
现场的大部分学生都选择α，小部分选择β
博弈论不能帮助我们选择人生目标，只能帮我们到达目标。换言之，人生的目标还是靠我们自己内心的认知和眼光大小
定义：
如果选择α得到的结果严格优于β，那么相对β是一个严格优势策略，重点在于：无论别人选什么，不要选择严格劣势策略
why？
学上A：因为每个人都会选择优势策略，而导致结果变糟，使总结果变糟
学生B：“你永远不会赢”
学生C：收益降低。
协和谬误
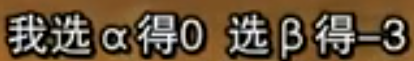
恶魔饭桶和愤怒天使的博弈
假设我们是恶魔饭桶：
这里我还是选择α，因为对于我们是优势策略。
假设相反，我们是愤怒天使：
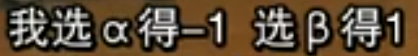
对我们来说选择α并不优于β，但是我们还是选择α，因为对于对方来说选择α是优势策略，所以对方大概率会选择α。
结论：分析博弈的最好方法，也就是策略分析的核心是：换位思考
社会调查：
70%选择α
30%选择β
学生A：选择β会使平均分升高。
学生B：长期博弈选β，收益大于α。
第二个游戏
ex，total = 5
5， 25， 60
ave = 30
win = 25
money = 5-0.05=4.95
多个玩家胜利，大家平分奖金
第一节课的五个结论
博弈论于现实世界是紧密联系的
跳出思维定势：制定协议（改变收益）
博弈的要素
组成：
游戏1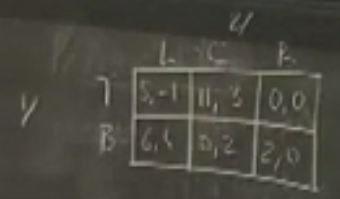
收益分配为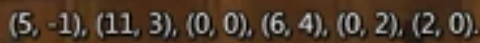
这里的I和II都没有优势策略
游戏2
大多数学生选择防守平坦的路
但是这个并不是一个合理的答案。
学生原因：人为中心地认为侵略者会选择平坦的那条路，以维持士兵数量的最大化。
我们要从对面的角度进行思考，对于侵略者（汉尼拔）而言
弱优于：它意味着选择平坦之途较选择崎岖之途而言至少要同样的好，可能还稍微好些
回归上期的数学游戏
大概有9个人选择了32,33,34。
有一个人选择了30，原因是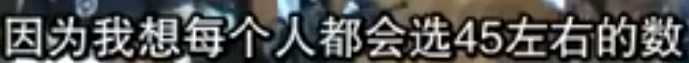
而大家会选笔比那小的，所以他就选择了一个更小的。
老师解释选择33的原因是，如果大家在【1,100】中随机选择，平均数会是50左右，50的2/3就是33.
然而学生并不会随机选择，所以最终数字会比33小，然后大概有12个人选择了22，因为33的2/3==22
.
选择直接剔除策略：“没有人会选择大于50的数”
如果每个人都选择100的话，最后的数为67，但是实时上不会，所以直接剔除掉67-100的数字。得出“没人会选择67以上的数”可以推出下一个结论“大于45的数会被剔除”。
意识到别人不会选择劣势策略之后，我们本身也不应该选择劣势策略。
然后剔除劣势策略，也就是再×2/3,然后得出30到45的数也被剔除，然后....
：我知道一件事，你也知道这件事，你知道我知道这件事，我也知道你知道这件事，以此类推，一个无限的循环 。
最后地，最优策略就是1，然后大部分同学选择了1，最后的结果是9.（平均数为13又1/3，2/3为9）有9个人选择了9
这个游戏的最终结果逐年下降。
最后强调一下共同知识：让两个上台，分别给两个带上帽子。他们知道对方帽子的颜色，但是不知道自己帽子的颜色，所以尽管他们知道至少有一人带着粉色的帽子，这个是相互知识。相互知识并不是公共知识。
共同知识并不只是我饿知道什么，还有我是否知道别人知道我知道别人知道。。。。以此类推
原文：https://www.cnblogs.com/hengge/p/12198399.html