前言：期末考试过后的死亡体验
看来我还是太菜了呢（误）
第一题 谁能拿最多奖学金
描述
某校的惯例是在每学期的期末考试之后发放奖学金。发放的奖学金共有五种，获取的条件各自不同：
1) 院士奖学金，每人8000元，期末平均成绩高于80分（>80），并且在本学期内发表1篇或1篇以上论文的学生均可获得；
2) 五四奖学金，每人4000元，期末平均成绩高于85分（>85），并且班级评议成绩高于80分（>80）的学生均可获得；
3) 成绩优秀奖，每人2000元，期末平均成绩高于90分（>90）的学生均可获得；
4) 西部奖学金，每人1000元，期末平均成绩高于85分（>85）的西部省份学生均可获得；
5) 班级贡献奖，每人850元，班级评议成绩高于80分（>80）的学生干部均可获得；
只要符合条件就可以得奖，每项奖学金的获奖人数没有限制，每名学生也可以同时获得多项奖学金。例如姚林的期末平均成绩是87分，班级评议成绩82分，同时他还是一位学生 干部，那么他可以同时获得五四奖学金和班级贡献奖，奖金总数是4850元。现在给出若干学生的相关数据，请计算哪些同学获得的奖金总数最高（假设总有同学能满足获得奖学 金的条件）。
输入
输入文件scholar.in的第一行是一个整数N（1 <= N <= 100），表示学生的总数。接下来的N行每行是一位学生的数据，从左向右依次是姓名，期末平均成绩，班级评议成绩，是 否是学生干部，是否是西部省份学生，以及发表的论文数。姓名是由大小写英文字母组成的长度不超过20的字符串（不含空格）；期末平均成绩和班级评议成绩都是0到100之间 的整数（包括0和100）；是否是学生干部和是否是西部省份学生分别用一个字符表示，Y表示是，N表示不是；发表的论文数是0到10的整数（包括0和10）。每两个相邻数据项之 间用一个空格分隔。
输出
输出文件scholar.out包括三行，第一行是获得最多奖金的学生的姓名，第二行是这名学生获得的奖金总数。如果有两位或两位以上的学生获得的奖金最多，输出他们之中在输入 文件中出现最早的学生的姓名。第三行是这N个学生获得的奖学金的总数。
样例输入
4
YaoLin 87 82 Y N 0
ChenRuiyi 88 78 N Y 1
LiXin 92 88 N N 0
ZhangQin 83 87 Y N 1
样例输出
ChenRuiyi
9000
28700
水题目不解释 直接结构体模拟if就过了
然后大粗心怪就被WA了一个点
注意输出的时候相同分数按出现顺序输出
用一个num变量保存操作就行啦
#include<bits/stdc++.h> using namespace std; const int MAXN=1e5+1; int read(){ int ans = 0, f = 1; char ch=getchar(); while(!isdigit(ch)) f*=(ch==‘-‘)?-1:1,ch=getchar(); do ans=(ans<<1)+(ans<<3)+(ch^48),ch=getchar(); while(isdigit(ch)); return ans*f; } struct node{ string name; int grade1;//平均 int grade2;//评议 char gan; char west; int book; int all; int num; }a[MAXN]; bool cmp(node x,node y){ if(x.all==y.all)return x.num<y.num; return x.all>y.all; } int main(){ int n=read(); for(int i=1;i<=n;i++){ cin>>a[i].name>>a[i].grade1 >>a[i].grade2 >>a[i].gan >>a[i].west >>a[i].book; a[i].num=i; } for(int i=1;i<=n;i++){ if(a[i].grade1>80&&a[i].book>=1)a[i].all+=8000; if(a[i].grade1>85&&a[i].grade2>80)a[i].all+=4000; if(a[i].grade1>90)a[i].all+=2000; if(a[i].west==‘Y‘&&a[i].grade1>85)a[i].all+=1000; if(a[i].grade2>80&&a[i].gan==‘Y‘)a[i].all+=850; } sort(a+1,a+n+1,cmp); cout<<a[1].name<<endl; cout<<a[1].all<<endl; int alll=0; for(int i=1;i<=n;i++)alll+=a[i].all; cout<<alll; return 0; } /*4 YaoLin 87 82 Y N 0 ChenRuiyi 88 78 N Y 1 LiXin 92 88 N N 0 ZhangQin 83 87 Y N 1*/
第二题 过河
描述
在河上有一座独木桥，一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子，青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数，我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点：0，1，……，L（其中L是桥的长度）。坐标为0的点表示桥的起点，坐标为L的点表示桥的终点。青蛙从桥的起点开始，不停的向终点方向跳跃。一次跳跃的距离是S到T之间的任意正整数（包括S,T）。当青蛙跳到或跳过坐标为L的点时，就算青蛙已经跳出了独木桥。
题目给出独木桥的长度L，青蛙跳跃的距离范围S,T，桥上石子的位置。你的任务是确定青蛙要想过河，最少需要踩到的石子数。
输入
输入文件river.in的第一行有一个正整数L（1 <= L <= 109），表示独木桥的长度。第二行有三个正整数S，T，M，分别表示青蛙一次跳跃的最小距离，最大距离，及桥上石子的个 数，其中1 <= S <= T <= 10，1 <= M <= 100。第三行有M个不同的正整数分别表示这M个石子在数轴上的位置（数据保证桥的起点和终点处没有石子）。所有相邻的整数之间用一 个空格隔开。
输出
输出文件river.out只包括一个整数，表示青蛙过河最少需要踩到的石子数。
样例输入
10
2 3 5
2 3 5 6 7
样例输出
2
考试时:一眼DP啊有木有 瞬间推出转移方程啊
发现L的范围后：好像线性dp会超时
试图优化：单调队列？斜率优化？我都学了啥来着？
最终：算了算了先搁着拿30分暴力分我先去拿后面的暴力分（我还是应该优化的）
结果在OJ上只水了11分...
题解：
当前的点ii只与它前i−j个点有关(s≤j≤t)
如果当前的点是石头那么就是所有到达该点的位置所需踩的最少石头数加1
经过上述的分析我们就可以得出我们的状态转移方程了：
该点为石头： dp[i] = min(dp[i],dp[i-j] +1)(s\leq j\leq t)dp[i]=min(dp[i],dp[i−j]+1)(s≤j≤t)
该点不为石头： dp[i] = min(dp[i],dp[i-j])(s\leq j\leq t)dp[i]=min(dp[i],dp[i−j])(s≤j≤t)
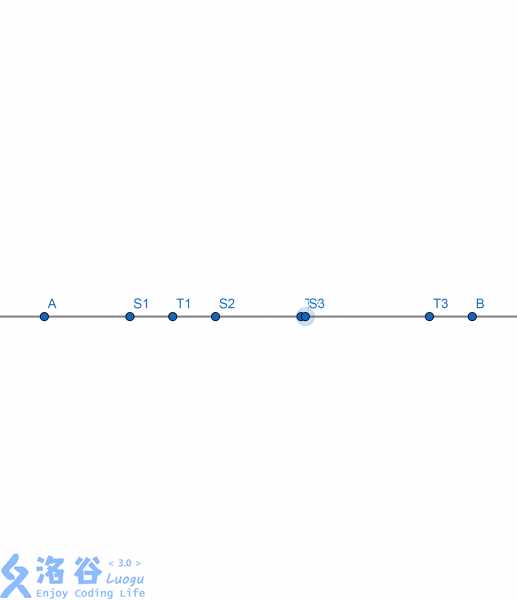(图片来自洛谷)
其中[Si?,Ti?]就是青蛙可以到的区间。 可以发现当s < t时， s和t一定会重合（当距离为lcm(s,t)即s，t的最小公倍数时） 而这以后的每个点都可以到达， 所以我们只需将每两个石头超过 s×t 的距离缩成s×t就可以了当然如果你有疑虑的话也可以开大一点。
当s=t时我们只需枚举每个石头的坐标是否为s的倍数即可
总结：利用石头数量少离散化石头排布优化线性DP
#include<bits/stdc++.h> #define ll long long using namespace std; const ll MAXN=300 * 105; ll read(){ ll ans = 0, f = 1; char ch=getchar(); while(!isdigit(ch)) f*=(ch==‘-‘)?-1:1,ch=getchar(); do ans=(ans<<1)+(ans<<3)+(ch^48),ch=getchar(); while(isdigit(ch)); return ans*f; } ll L; ll S,T,M; int Nx[MAXN],a[MAXN]; int vis[MAXN],dp[MAXN]; int all; int main(){ L=read(); S=read(); T=read(); M=read(); int lcm=S*T; for(int i=1;i<=M;i++){ Nx[i]=read(); } sort(Nx+1,Nx+M+1); if(S==T){ int cnt=0; for(int i=1;i<=M;i++) if(Nx[i]%S==0)all++; cout<<all<<endl; return 0; } for(ll i=1;i<=M;i++){ int len=Nx[i]-Nx[i-1]; if(len>=lcm)len=lcm; a[i]=a[i-1]+len; vis[a[i]]=1; } L=a[M]+lcm; memset(dp,0x7f,sizeof(dp)); dp[0]=0; for(int i=1;i<=L;i++) for(int j=S;j<=T;j++) { if(i-j>=0)if(vis[i])dp[i] = min(dp[i - j] + 1,dp[i]); else dp[i] = min(dp[i - j],dp[i]); } int ans=0x7f; for(int i=a[M];i<=L;++i)ans=min(ans,dp[i]); cout << ans << endl; return 0; }
第三题 篝火晚会
描述
佳佳刚进高中，在军训的时候，由于佳佳吃苦耐劳，很快得到了教官的赏识，成为了“小教官”。在军训结束的那天晚上，佳佳被命令组织同学们进行篝火晚会。一共有n个同学， 编号从1到n。一开始，同学们按照1，2，……，n的顺序坐成一圈，而实际上每个人都有两个最希望相邻的同学。如何下命令调整同学的次序，形成新的一个圈，使之符合同学们的 意愿，成为摆在佳佳面前的一大难题。
佳佳可向同学们下达命令，每一个命令的形式如下：
(b1, b2,... bm -1, bm)
这里m的值是由佳佳决定的，每次命令m的值都可以不同。这个命令的作用是移动编号是b1，b2，…… bm –1，bm的这m个同学的位置。要求b1换到b2的位置上，b2换到b3的位置 上，……，要求bm换到b1的位置上。
执行每个命令都需要一些代价。我们假定如果一个命令要移动m个人的位置，那么这个命令的代价就是m。我们需要佳佳用最少的总代价实现同学们的意愿，你能帮助佳佳吗？
输入
输入文件fire.in的第一行是一个整数n（3 <= n <= 50000），表示一共有n个同学。其后n行每行包括两个不同的正整数，以一个空格隔开，分别表示编号是1的同学最希望相邻 的两个同学的编号，编号是2的同学最希望相邻的两个同学的编号，……，编号是n的同学最希望相邻的两个同学的编号。
输出
输出文件fire.out包括一行，这一行只包含一个整数，为最小的总代价。如果无论怎么调整都不能符合每个同学的愿望，则输出-1。
样例输入
4
3 4
4 3
1 2
1 2
样例输出
2
考场拿到实属懵逼
搜索？显然超时
环？图论？
动态规划？贪心？找不出思路...
最后瞎写了一堆模拟试图强行拿分（标准蒟蒻）
题解：认真读题，发现我们要从一个状态转换到满足目标的另一个状态
所求结果就是到达目标所需要的最小转换次数
还有个很坑的点——m个人可以不连续！！！！
这个锅题目描述得背，描述里b1,b2,...bm实在是太规则了，使我以为操作必须得从1开始，并且要连续...
那么首先我们需要先构建出来目标环。但是环不好处理，我们需要断环为链。但是断环为链显然是有两种情况，所以我们需要构建两个链。
eg.比如说样例的两种链情况：
1、2、4、3
1、3、2、1
然后有个结论就是：
构建完链之后按照上述规律来个check就可以了。
#include<bits/stdc++.h> using namespace std; const int MAXN=50000+10; using namespace std; inline int read()//读入优化 不用写 { char ch=‘*‘; while(!isdigit(ch=getchar())); int num=ch-‘0‘; while(isdigit(ch=getchar()))num=num*10+ch-‘0‘; return num; } int n; int le[MAXN],ri[MAXN]; int c[MAXN],isc[MAXN]; int main(){ n=read(); for(int i=1;i<=n;i++)le[i]=read(),ri[i]=read(); c[1]=1; c[2]=le[1]; for(int i=1;i<=n;i++){ if(ri[le[i]]!=i&&le[le[i]]!=i||le[ri[i]]!=i&&ri[ri[i]]!=i){ cout<<-1; return 0; } if(le[c[i]]==c[i-1])c[i+1]=ri[c[i]]; else c[i+1]=le[c[i]]; } int ans=n+10; for(int i=1;i<=n;i++){//找旋转次数 若旋转次相同视为与序列相同 即为不用换位置的个数 isc[((i-c[i]+n))%n]++; ans=min(ans,n-isc[((i-c[i]+n))%n]); } memset(isc,0,sizeof(isc));//重新初始化 反跑一遍 memset(c,0,sizeof(c)); c[0]=1; c[1]=ri[1]; for(int i=1;i<=n;i++){ if(ri[c[i]]==c[i-1])c[i+1]=le[c[i]]; else c[i+1]=ri[c[i]]; } for(int i=1;i<=n;i++){ isc[((i-c[i]+n))%n]++; ans=min(ans,n-isc[((i-c[i]+n))%n]); } cout<<ans; return 0; }
第四题 等价表达式
描述
明明进了中学之后，学到了代数表达式。有一天，他碰到一个很麻烦的选择题。这个题目的题干中首先给出了一个代数表达式，然后列出了若干选项，每个选项也是一个代数表 达式，题目的要求是判断选项中哪些代数表达式是和题干中的表达式等价的。
这个题目手算很麻烦，因为明明对计算机编程很感兴趣，所以他想是不是可以用计算机来解决这个问题。假设你是明明，能完成这个任务吗？
这个选择题中的每个表达式都满足下面的性质：
1． 表达式只可能包含一个变量‘a’。
2． 表达式中出现的数都是正整数，而且都小于10000。
3． 表达式中可以包括四种运算‘+’（加），‘-’（减），‘’（乘），‘^’（乘幂），以及小括号‘(’，‘)’。小括号的优先级最高，其次是‘^’，然后是‘’，最 后是‘+’和‘-’。‘+’和‘-’的优先级是相同的。相同优先级的运算从左到右进行。（注意：运算符‘+’，‘-’，‘*’，‘^’以及小括号‘(’，‘)’都是英文字符）
4． 幂指数只可能是1到10之间的正整数（包括1和10）。
5． 表达式内部，头部或者尾部都可能有一些多余的空格。
下面是一些合理的表达式的例子：
((a^1) ^ 2)^3，aa+a-a，((a+a))，9999+(a-a)a，1 + (a -1)^3，1^10^9……
输入
输入文件equal.in的第一行给出的是题干中的表达式。第二行是一个整数n（2 <= n <= 26），表示选项的个数。后面n行，每行包括一个选项中的表达式。这n个选项的标号分别 是A，B，C，D……
输入中的表达式的长度都不超过50个字符，而且保证选项中总有表达式和题干中的表达式是等价的。
输出
输出文件equal.out包括一行，这一行包括一系列选项的标号，表示哪些选项是和题干中的表达式等价的。选项的标号按照字母顺序排列，而且之间没有空格。
样例输入
( a + 1) ^2
3
(a-1)^2+4*a
a + 1+ a
a^2 + 2 a 1 + 1^2 + 10 -10 +a -a
样例输出
AC
提示
对于30%的数据，表达式中只可能出现两种运算符‘+’和‘-’；对于其它的数据，四种运算符‘+’，‘-’，‘*’，‘^’在表达式中都可能出现。对于全部的数据，表达式中 都可能出现小括号‘(’和‘)’。
首先我们很可以很容易想到用特殊值替代题目中的常量a
但是这并没有什么用
这道题的难点在于细节的处理和逻辑推理
考场能AC的都是什么怪物啊啊
题解：
第一，这道题存在左、右括号不匹配的情况。
第二，gets可能是不能正常使用的。//感谢网上大佬的快读
第三，当我们将字符a代入之后，由于答案会爆long long，所以需要取模。然而当我们在做减法的时候，由于我们已经进行了模运算，所以两个余数的大小是未知的，于是我们要在减后加上取模的那个数（我用的1e9+7），然后再取模，这样就不会出现负数的情况了。
总结：我们用栈来保存式子 通过分析运算优先级 计算栈顶和特殊值处理过掉这道题
思路大致如此 代码也很好实现呢
加了一些注解 看懂应该没啥问题
#include<cstdio> #include<cstring> #define LL long long const int M=1e9+7; LL n,i,p,topn,topf,len,k; char a[51]; LL num[51]; char f[51]; LL t[11]={0,41,71,83,91,101}; LL ans[11]; char c[51]; LL quickpow(LL a,LL b,LL p)//快速幂 { LL s=1; a%=p; for(;b;b>>=1,a=(a*a)%p) if(b&1) s=(s*a)%p; return s; } LL level(char c)//对运算优先级排序 { if(c==‘(‘) return 0; if(c==‘+‘||c==‘-‘) return 1; if(c==‘*‘||c==‘/‘) return 2; if(c==‘^‘) return 3; return 0; } void work()//计算栈顶 { LL x=num[topn--]; LL y=num[topn--]; char c=f[topf--]; if(c==‘+‘) num[++topn]=(x+y)%M; else if(c==‘-‘) num[++topn]=(y-x+M)%M;//注意＋M else if(c==‘*‘) num[++topn]=(x*y)%M; else if(c==‘^‘) num[++topn]=quickpow(y,x,M); } void getnum(char a[],LL &p)//把变量a改为常数 { LL t=0; while(a[p]>=‘0‘&&a[p]<=‘9‘) t=(t*10+a[p++]-48)%M; num[++topn]=t; } void push(LL n)//将字符a用第n个数进行替换 { num[++topn]=t[n]; } LL solve(char a[],LL i) { p=topf=topn=0; len=strlen(a); while(p<=len-1) if(a[p]>=‘0‘&&a[p]<=‘9‘) getnum(a,p); else if(a[p]==‘ ‘) p++; else if(a[p]==‘+‘||a[p]==‘-‘||a[p]==‘*‘||a[p]==‘/‘||a[p]==‘^‘) if(level(a[p])>level(f[topf])) f[++topf]=a[p++]; else { while(level(a[p])<=level(f[topf])) work(); f[++topf]=a[p++]; } else if(a[p]==‘a‘) { push(i); p++; } else if(a[p]==‘(‘) f[++topf]=a[p++]; else if(a[p]==‘)‘) { bool bb=0; for(int i=1;i<=topf;i++) if(f[i]==‘(‘) bb=1; if(!bb) { p++; continue; } while(f[topf]!=‘(‘) work(); topf--; p++; } while(topn!=1) work(); return num[1]; } void get(char a[]) { for(int i=0;i<=50;i++) a[i]=‘\0‘; char c=getchar(); int pos=0; while(c==‘\n‘||c==‘\r‘) c=getchar(); while(c!=‘\n‘&&c!=‘\r‘) { a[pos++]=c; c=getchar(); } } int main() { get(a);//不能用gets 自己写一个快读 for(i=1;i<=5;i++) ans[i]=solve(a,i); scanf("%I64d\n",&n); for(k=1;k<=n;k++) { get(c); bool b=1; for(i=1;i<=5;i++) if(solve(c,i)!=ans[i]) { b=0; break; } if(b) putchar(‘A‘+k-1); } }
最后恭喜自己的第一篇博客写好了
by:Liberty358
附上一张老婆图片结个尾
原文：https://www.cnblogs.com/Heartbeat358/p/12203187.html