高数学习笔记

1. \[ \frac{a_0 + a_1x + a_2x^2 + a_3x^3 + \dots+a_nx^n}{b_0 + b_1x + b_2x^2 + b_3x^3 + \dots+b_nx^n} x-->inf\case1 : n = m \ \ \ \frac{a_n}{b_m}\case2 : n > m \ \ \ \ inf\case3 : n < m \ \ \ \ 0 \]
2. \[ (1 + \frac{1}{n})^n = e \ \\ \ n -->inf \]

3. \[ \frac{sinx}{x} = 1\x-->0 \]
   4.连续不一定可导 ， 可导一定连续。

4. 常用导数

编号	原函数	导函数
①
②
③
④
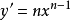⑤
⑥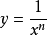
⑦
⑧
⑨
⑩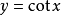
?
?
?
?
?
?
?	（双曲函数）	（双曲函数）

6 洛必达法则

用于在 0 ， INF 之类的地方求导 。

就是一直求导直到能够判断谁大谁小位置 。

7 偏导 ， 就是左趋近 ， 右趋近 ，

8 隐函数求导 ， 将 y 写成f(x)的形式强行带入 ， 将他化简。

9 左导右导都存在 ， 但是方向不同 ， 则在该位置不可导 。

高数听课笔记

原文：https://www.cnblogs.com/R-Q-R-Q/p/12207708.html